多想少算视角下的2018年高考数学试题分析*
2019-10-29四川内江师范学院数学与信息科学学院641112刘成龙
四川内江师范学院数学与信息科学学院(641112) 刘成龙 胡 琳 张 庆
数学作为思维的科学,其核心价值在于发展学生的数学思维能力.数学思维的本质就是想问题和想问题如何解决.[1]因此,高考数学命题将“多一点想,少一点算”作为了一条基本的命题理念.[2]其中,想即思考,算即运算,通过思考来指导运算,从而达到少算、巧算.在此理念的指导下,“多想少算”成为了高考命题的基本原则.研究表明,2018年高考命题充分体现了“多想少算”这一原则.如何在解题中实现“多想少算”呢? 运用恰当的策略是实现“多想少算”的最佳路径.文中以2018年高考试题为例,介绍实现“多想少算”的几种解题策略,以期读者充分感受“多想少算”的命题理念和策略的魅力.
策略一、利用定义
数学概念是反映现实世界空间形式和数量关系本质属性的思维形式.李邦河院士希望“喜欢数学的人千万要重视基本概念,不仅要记住,还要通过具体的例子来深入的理解”.李院士还认为:数学根本上是玩概念的,而不是纯粹的技巧.[3]高考数学十分注重对定义的考查,同时借助定义能快速得到问题的解.
例1(2018年高考浙江卷第8 题) 已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则( )
A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1
C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

图1
解如图1,设O为正方形ABCD的中心,M为AB中点.过E作EF//BC,且交CD于F,过O作ON⊥EF于N,连接SO,SN,OM,OE,则SO⊥面ABCD,OM⊥AB.于是∠SEN=θ1,∠SEO=θ2,∠SMO=θ3,从而因为SN ≥SO,EO ≥OM,所以tanθ1≥tanθ3≥tanθ2,即θ1≥θ3≥θ2,故选D.
评析本例重点考查学生对异面直线成角、线面角、二面角定义的理解.解答本例只需要紧扣三种角的定义,通过作辅助线找出三种角,再通过简单运算即可.这一过程充分体现了定义是思维之母,思维是运算之基.
策略二、利用“二手结论”
“二手结论”指除高中教材中现有结论之外的结论.高中阶段有大量的“二手结论”,比如:函数的点对称、线对称、周期结论、向量的极化恒等式结论、三角形面积的向量表示结论等等.利用“二手结论”解题,可以缩短推演时间、大大简化运算.
例2(2018年高考全国ⅠⅠⅠ卷理科第16 题) 已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B,两点.若∠AMB=90°,则k=___.
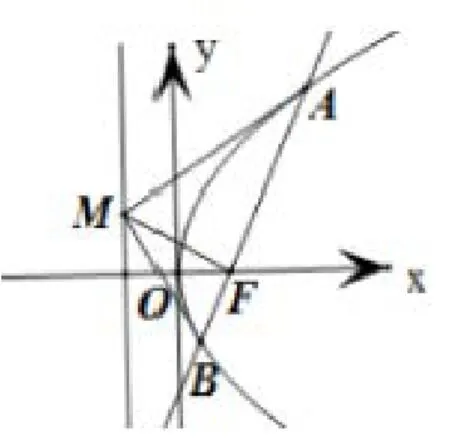
图2
分析如图2,与本例直接相关的结论有:过抛物线y2=2px(p>0)焦点F的直线交抛物线于A,B两点,M为准线上一点,且∠AMB=90°,则MF⊥AB.利用该结论可以秒杀例2,具体解答过程参见文[4].
例3(2018年高考全国ⅠⅠⅠ卷理科第20 题)已知斜率为k的直线l与椭圆C:交于A,B两点.线段AB的中点为M(1,m)(m>0).
(ⅠⅠ)设F为C的右焦点,P为C上一点,且证明:成等差数列,并求该数列的公差.
分析与本例直接相关的“二手结论”是焦半径公式:已知P(x0,y0) 是椭圆上一点,分别为椭圆的左右焦点,则
解(ⅠⅠ) 设A(x1,y1),B(x2,y2),P(x3,y3),则于 是因为M(1,m) 为AB的中点,所以x1+x2=2,于是x3=1.由焦半径公式得所以故即成等差数列(此处省略公差的求解).
例4(2018年高考全国卷Ⅰ理科第21 题) 已知函数若f(x)存在两个极值点x1,x2,证明:
分析与本例直接相关的“二手结论”是对数—平均值不等式:已知x1,x2>0,且则
解(ⅠⅠ)因为则x1,x2是的两实数根,于是a>2,x1x2=1,所以由对数—平均值不等式可得:
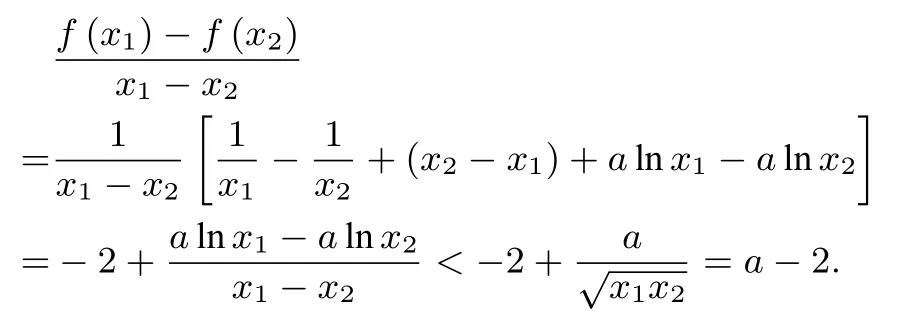
评注例2、3、4 的解答中,充分运用“二手结论”实现了问题解答的优化.具体来讲,例2 解答中用到的结论常在一些练习题和模拟试题中出现;例3 中用到的焦半径公式在教材正文部分没有出现,但运用阅读材料中的第二定义能轻松得到;例4 中用到的对数—平均不等式是数学竞赛的内容,但已经成为高考解题的重要工具.因此,高三复习中要关注教材、模拟试题、以及竞赛中的一些重要结论.当然,并不需要对所有结论都加以记忆,这样会加重学生负担,但结论本身是一个数学问题,结论的推导过程就是问题的解决过程.因此,经典结论需要记忆,一般结论需要弄清解答过程.
策略三、利用补形法
所谓补形法,是将一几何体补成另一几何体后,在所形成的新几何体中研究原几何体中的有关元素位置关系及其计算的方法,也称嵌入法[5].补形法蕴含了转化的思想,补形的过程中往往具有创造的成分.
例5(2018年高考全国ⅠⅠⅠ卷理科第19 题) 如图3,边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直,M是上异于C,D的点.

图3
(ⅠⅠ)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.
解[4](ⅠⅠ)将图3补形成直三棱柱.当M位于的中点时三棱锥M-ABC体积最大.面MAB与面MCD所成二面角为∠APD.于是故面MAB与面MCD所成二面角的正弦值为
评析解答本例的方法有多种,比如:向量法、几何法(定义法)等等.具体来讲,向量法涉及建系、坐标化、求法向量等过程,尽管有规可依,但是运算过程较为复杂;几何法解答需要找出二面角,这需要找交线、做垂线,但交线没有现成的,且作出的二面角需要借助“三垂线”定理来证明,过程较繁琐.通过补形使得原问题的本质得以充分的展示,优化了问题的解答,充分体现了多一点想,少一点算.
策略四、利用模型
数学模型是研究者依据研究目的,将所研究客观事物的过程和现象的主要特征、主要关系,采用形式化的数学语言,概括或近似地表达出来的一种结构.[6]比如:指数模型、对数模型、三角模型、最优化模型、微分方程模型等等.数学模型代表了解决一类问题的思考方式和模式.利用模型能缩短思考时间、提升解题效率.
例6(2018年高考上海卷第12 题) 已知实数x1,x2,y1,y2满足:x21+y12=1,x22+y22=1,x1x2+y1y2=,则的最大值为___.

图4
分析由和结构特征联想到点到直线距离公式这一基本模型.
解如图4,P(x1,y1),Q(x2,y2)在x2+y2=1 上.由得∠POQ=则ΔPOQ为等边三角形.表示点P(x1,y1),Q(x2,y2) 到直线l1:x+y-1=0 的距离的和.
设∠PON=α,所以
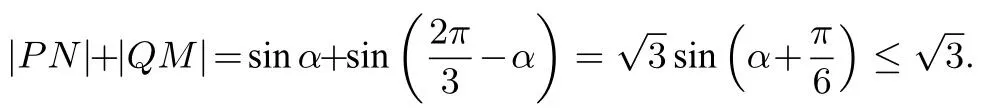
评析解答本例的核心是将视为点到直线的距离和,这蕴含了模型化思想.同时,将代数问题几何化,使得问题更加直观、形象,体现了数与形的辩证统一.总之,立足模型,利用图形表征问题、分析问题、解决问题是解法的最大亮点.
策略五、利用高等工具
高等工具指高等数学中的定理、公式、法则等知识.近年来,越来越多的高考试题含有高等数学背景.因此,高等工具成为了解答这一类试题的有力工具.常见的高等工具有洛必达法则、Jensen 不等式、泰勒展式、拉格朗日中值定理、不动点理论等等.
例7(2018年高考全国卷ⅠⅠⅠ文科第21 题) 已知函数
(ⅠⅠ)证明:当a ≥1 时,f(x)+e ≥0.
证明欲证f(x)+e=≥0,只需证明由泰勒公式有可得ex ≥x+1,于是ex+1≥x+2.故又因为a ≥1,所以ax2+2x+1≥x2+2x+1=(x+1)2≥0.所以当a ≥1 时,f(x)+e ≥0.
评注本例的初等解法涉及繁琐运算和放缩,运用泰勒公式将ex+1放缩为ex+1≥x+2,这一步可以看成是去超越式,使得解答思维难度和运算量降低了,这充分展示了高等工具的威力.特别指出,在历年的高考阅卷中,运用高等工具解答高考试题只要做到有理有据均没有扣分.
例8(2018年高考全国卷ⅠⅠⅠ理科第21 题) 已知函数
(ⅠⅠ)若x=0 是f(x)的极大值点,求a.
分析本例(ⅠⅠ)问含有丰富的高等数学背景,比如:运用泰勒公式、洛必达法则、极大值点的第三充分条件、帕德逼近等.运用这些高等工具既能发现证明思路,又能给出直观、简洁的证明过程,具体过程可参见文[7].
策略六、利用特殊化
波利亚指出:“特殊化是从对象的一个给定集合,转而考虑那包含在这集合内的较小集合.”特殊化在问题解决、结论发现上具有积极意义,正如希尔伯特所说“在讨论数学问题时,我相信特殊化比一般化起着更重要的作用.”特殊化包括字母数据特殊、图形位置特殊、几何图形特殊化等等.
例9(2018年高考全国卷Ⅰ理科第10 题)图5来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为ⅠⅠ,其余部分记为ⅠⅠⅠ.在整个图形中随机取一点,此点取自Ⅰ,ⅠⅠ,ⅠⅠⅠ的概率分别记为p1,p2,p3,则( )
A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3
分析将直角△ABC特殊化为直角边为2 的等腰直角三角形.易得,p1=2,p2=2,p3=π —2.故p1=p2>p3,选A.
评注华罗庚教授指出:“善于退,一直退到原始而不失重要性的地方,是学习数学的一个诀窍.”特殊化即为退的一种形式.本例作为选择题,需要小题小做、快做、巧作,特殊化是最佳的解题策略.退回到直角边为2 的等腰直角三角形来解答本例,既直观,又方便运算.
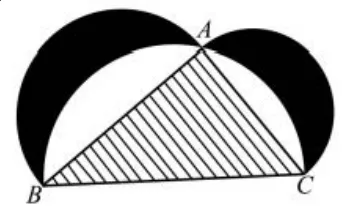
图5
策略七、利用合理分类
分类与整合思想是指将研究对象按照某个标准分成若干类,再分别对每一类进行解答,进而获得原问题的解.运用分类与整合思想的核心是分类.分类需要满足:(1)分类标准统一;(2)分类不重不漏;(3)分类不能越级.[8]合理的分类往往能简化问题的解答.
例10(2018年高考浙江卷第16 题)从1,3,5,7,9 中任取2 个数字,从0,2,4,6 中任取2 个数字,一共可以组成____个没有重复数字的四位数.(用数字作答)
解(1)选0 时,有C25C13C13A33=540 种;(2)不选0 时,有C25C23A44=720 种.所以共有540+720=1260 种不同的排法.
评析解答本例的关键是合理的分类:选0、不选0.解答中若不将是否选0 作为分类的标准,在处理中容易重、漏,以0 为分类标准能轻松地获得问题的解.
策略八、利用数形结合
数学家华罗庚指出“数无形时少直觉,形少数时难入微.数形结合百般好,隔离分家万事休.”可以看出数形结合是沟通代数、几何的重要方式.同时,数形结合可以降低复杂问题的思维难度,实现问题解决的优化.
例11(2018年高考北京卷理科第14 题) 已知椭圆双曲线1(m,n>0).若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为___;双曲线N的离心率为____.

图6
解如图6,∠AOF1=60°,∠AF1F2=60°,∠AF2F1=30°.所以ΔAF1F2为直角三角形.故不妨设AF1=1,则AF2=所以a=故椭圆的离心率又不妨设m=1,则n=双曲线离心率则e2=2.
策略九、利用极限法
极限法是指利用极限来分析问题、解决问题的方法.解答时将问题放置到极端状态或极端条件来分析,往往能优化问题的解答.
例12(2018年高考全国卷ⅠⅠ理科第3 题)函数f(x)=的图像大致为( )
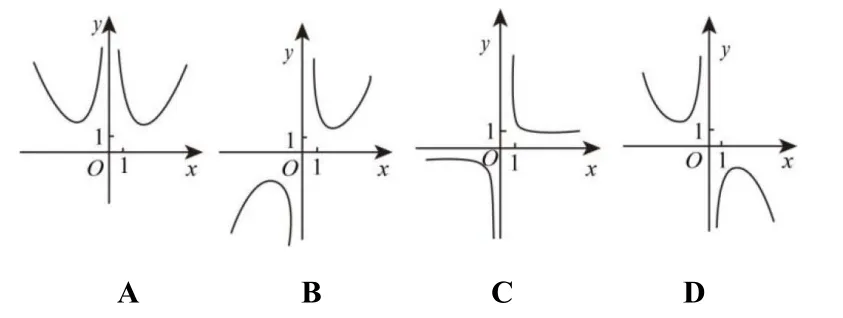
解析不妨从函数构成要件来思考:当x →+∞时,ex →+∞,e-x →0,x2→+∞,故=又因为指数函数比二次函数增长速率快得多,故因此,排除A、C、D 选项,选择B.同理,
