网络消费者信心与我国经济增长模型分析

李健　刘建民　李秋

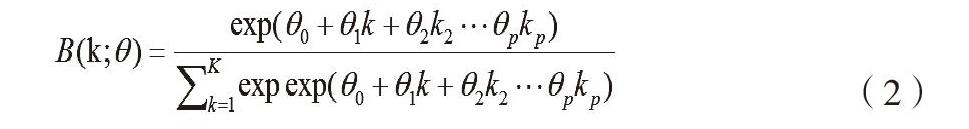
内容摘要：消费者信心指数是一个能够反映消费者消费趋向、预测经济运行情况的重要指标。本文以我国在2005-2017年的网络消费者信心指数（WCCI）和国民生产总值（GDP）作为分析对象，通过构建回归模型对网络消费信心与我国经济发展的关系进行研究。结果显示，对于我国网络消费者信心指数和国民生产总值数据来讲，采用基准模型和混合模型都可以證明两者之间存在较强的关联性;网络消费者信心指数对我国经济增长具有直接影响，在加入高频月度网络消费者信心指数后，模型的拟合效果得到改善;混频类模型的均方根误差低于自回归预测模型，预测效果优于自回归预测模型;混频模型能够有效地对网络消费者信心指数和经济增长之间的次序性进行拟合，避免了在频率转换过程中信息的缺失和错乱，具有充分提取有效信息的能力。

关键词：网络消费者信心   经济增长   基准模型   混合模型   混频回归模型

引言

在互联网高速发展的今天，信息传播速度日益加快，人们逐渐习惯于通过网络搜索来获取各个方面的信息，同时人们的消费方式也逐渐由传统的实体店消费转向线上消费，此时网络消费者信心便逐步成为衡量网络消费者消费倾向的新兴指标。目前，网络消费者信心这一指标主要是通过对网络信息搜索量、商品交易量、网民数量等多种数据综合分析而得出的。国内外众多专家从多个方面就网络搜索与消费者信心指数间的关联性进行了大量研究，发现在不同的经济市场环境下二者会发生不确定性的变化。其中，有学者以我国网络搜索数据作为反映消费者预期消费的指标，通过研究房地产价格的影响因素，认为该指标与房价变化存在先后次序关系;也有学者通过构建VAR模型分析了政府资金投入对网络消费者信心的影响，发现政府投入对网络消费者信心的影响具有不均衡性，政府扶持力度增大对居民消费水平提升的促进作用，弱于扶持力度减小对居民消费水平提升的阻碍作用。本文以已有文献研究结论为基础，通过构建回归模型来研究网络消费者信心与我国经济增长的关系，并基于高频网络消费者信心指数对国内生产总值进行预测，以期为我国经济的进一步发展提供参考。

变量选取与数据描述

本文选取2005-2018年我国网络消费者信心指数（WCCI）和国民生产总值（GDP）作为研究样本，并对数据进行描述性统计分析，分析结果如表1所示。可以看出，国家GDP标准差大于WCCI，说明前者波动性高于后者。WCCI的偏度是0.8552，GDP偏度为-0.0667，说明前者序列正偏，后者序列负偏。

本文对各变量进行ADF平稳性检验，检验结果如表2所示。可以看出，网络消费者信心指数和国民生产总值的P值分别为0.6288和0.6097，均高于临界值0.05，表明网络消费者信心指数和国民生产总值序列接受了存在单位根的原假设，对两指标进行一阶差分处理，其概率值均变成零，否定了原假设。因此，网络消费者信心指数与国民生产总值均为一阶单整序列。

网络消费者信心与我国经济增长的模型分析

本文以宏观经济预测模型作为基准模型，来判断MIDAS模型预测的优劣程度，且主要应用AR模型来对比分析低频和混频预测模型系数的似然对数、显著水平等，选取能够较好预测我国经济增长的模型。在此，本文构建了低频预测模型和多种混频模型，分别通过各模型对我国经济进行预测，并对低频和高频模型进行向前3步预测处理，最终选取预测效果最优的模型。

（一）传统AR模型的国民生产总值预测

本文构建低频国民生产总值分析模型。针对高频WCCI数据，本文采取求平均值的方法对其进行低频处理，进而使得网络消费者信心指数与国民生产总值均属于同一频率的季度数据。同时，采取重复比较赤池信息准则、施瓦茨等信息准则数值来确定模型的滞后阶数，将滞后阶数为1的模型（AR（1）模型）设定为预测基准模型。具体估计内容如表3所示。

通过表3可以得出，作为宏观变量，国民生产总值表现出明显的自相关性。经过详细分析，前一期的国民生产总值对本期国民生产总值存在显著的正面影响。模型的拟合优度为0.8026，对数极大似然值为8.9042，赤池信息准则数值为-0.4921，可以明确模型具有良好的拟合效果。对应的回归方程如下：

GDP=0.2526+0.8892GDPt-1                                          （1）

通过以上方程可以得出，当前一期国民生产总值提高或者降低1%时，本期的国民生产总值将会随之提高或者降低0.8892%。本文进一步对模型的残差进行描述性统计分析，描述结果如表4所示。

通过表4残差分析结果可得，模型残差的偏度值为-0.7054<0，表明残差序列存在负偏，向左拖尾。残差序列的峰度值为2.1793<3，模型残差表现出平稳趋势。残差序列的雅克贝拉统计量的P值为0.1785>0.05，表明残差序列服从正态分布。以上分析结果说明了AR（1）回归模型提取了充分且有效的信息。

（二）基于混频回归模型的国民生产总值预测

本文选取指数阿尔蒙多项式的权重函数来构建MIDAS模型，其中指数阿尔蒙多项式函数可以用如下方程表示：

（2）

在式（2）中，本文以θ1≤300、θ2<0对相关参数进行约束，以获取递减性的正权重函数，通过分析高频和低频在不同滞后阶数的预测效果，本文将MIDAS模型的最佳高频滞后阶数定为18，接下来对滞后阶数为18的高频模型进行估计，估计结果如表5所示。

各参数所表示的含义如下所示：

yt=β0+λyt-1+β1B（L1/m;θ）（1-λL）x（m）t-h+ε（m）t         （3）

式（3）中，λ为自回归项系数，β0为常数项，β1为高频模型相关系数，θ1和θ2为指数型阿尔蒙多项式中的预测系数。通过公式（3）来对表5中数据进行计算，可得出国民生产总值的具体表达形式：

GDP=1.7521-0.7206GDPt-1+0.5317B（L1/3;θ）WCCI（3）t-3+ε（3）t                                                                     （4）

β1顯著为正，表明网络消费者信心指数和经济增长之间具有显著的关联性，这主要是因为当消费者群体具有较大购买需要时，网络平台作为消费市场的主要部分，消费者商品购买需求的提升会促进网络消费水平的提升，相应的国民GDP也会出现升高。同时，通过对比分析一阶滞后模型与MIDAS（3，18）-AR（1）模型的赤池信息准则能够得知，赤池准则值小于AR（1）模型，表明MIDAS模型对各指标的预测效果要好于传统模型。本文对MIDAS（3，18）-AR（1）模型的残差进行描述性统计分析，分析结果如表6所示。

通过表6统计结果可得，相对来说MIDAS模型残差的标准差小于AR（1）模型，这表明针对残差的波动性来讲，AR（1）模型残差的波动性要强于MIDAS模型。残差的偏度为-0.4582<0，说明残差序列负偏，向左拖尾。残差序列的峰度为1.9553<3，也低于AR（1）模型残差峰度，这表明MIDAS模型中残差的平稳性要好于AR（1）模型。残差的雅克贝拉统计量概率为0.4117，远远高于临界值0.05，表明残差序列基本服从正态分布，这也说明了通过月度网络消费者信心指数对季度国民生产总值序列做出的MIDAS模型搜集了必要的信息。在此，本文以MIDAS（3，18）-AR（1）模型为基础，进一步拟合出MIDAS（3，18，3）-AR（1）模型，并对其精度进行预测，具体预测结果如表7所示。

通过表7预测结果可以得知，在参入高频月度网络消费者信心这一指标条件下，与一阶滞后模型相比较，均方根误差、平均绝对百分误差和Theil不等系数等估计效果所对应的指标都呈现出降低，三步向前预测模型的估计效果显著优于一阶滞后模型，混频估计模型表现出良好的估计效果，其估计效果相较于相等频率的其他模型来讲更加具有优势。

本文构建无约束MIDAS模型U-MIDAS（3，18），以对比分析有限制和无限制MIDAS模型的估计效果。经过以上描述性统计分析之后，本文确定模型的滞后期为18，模型的优劣评价指标如表8所示。

通过表8评价结果可以得出，在对U-MIDAS（3，18）-AR（1）模型进行对数处理后，其极大似然值超过了MIDAS模型的极大似然值，同时赤池信息准则和贝叶斯准则值变小，说明U-MIDAS（3，18）-AR（1）模型的拟合效果要明显优于指数型阿尔蒙多项式。

通过表9统计结果可以得出，无约束估计测模型残差的标准差低于MIDAS模型，说明前者模型残差较后者更加趋于平稳。同时，其残差的偏度为0.6225>0，此时残差序列正偏，向右拖尾。残差序列的峰度为1.9535<3，说明残差比较平缓。残差的雅克贝拉统计量P值为0.3617>0.05，表明该模型残差序列符合正态分布，这也进一步说明无约束模型对各指标数据具有良好的预测效果。本文又进一步对无约束估计模型进行三步向前预测，具体预测结果如表10所示。通过表10评价结果能够得到，当模型待估系数不受约束后，无论是一阶滞后模型还是指数型阿尔蒙混频数据模型，其均方根误差、平均绝对误差、平均绝对百分误差率等估计指标均出现了明显下降，模型对数据估计的准确性得到了提升，这反映出在估计我国国民生产总值时，非限制性混频数据模型相比于其他模型，更符合国民生产总值及网络消费者信心指数的数据特点，预测效果更为理想。

（三）AR（1），MIDAS与U-MIDAS模型结果的比较与评价

本文对AR（1）、MIDAS和U-MIDA模型和预测的各项指标进行综合对比，对比结果如表11所示。

分别就各模型的拟合结果来分析，混频类模型对数据的拟合结果比低频模型更加能反映真实情况，虽然指数型阿尔蒙多项式混频数据模型的R2和对数极大似然值均小于一阶滞后模型，但其赤池信息准则值却小于一阶滞后模型，尤其是解除约束的混频数据模型，其R2、赤池信息准则等指标均优于一阶滞后模型，这表明通过模型的拟合效果等角度来看，采取混频模型来分析网络消费者信心和经济发展的效果较一阶滞后模型更加良好。

结论

就我国网络消费者信心指数和国民生产总值数据而言，通过基准模型和混合模型可以证明二者之间存在一定关联性;混频模型对网络消费者信心指数和经济增长之间的次序性具有良好的拟合效果，减少了在频率转换过程中信息的丢失和错乱，能够充分提取有效信息;混频数据模型在没有相关权重多项式限制的条件下，模型的预测结果更加真实，且拟合效果明显优于阿尔蒙多项式混频数据模型。

网络消费者信心指数与我国经济发展具有较强的关联性，在加入高频月度网络消费者信心指数后，模型拟合效果有所改善;混频类模型的均方根误差小于AR（1）模型，预测效果相较于自回归预测模型更优。与自回归模型相比，混频模型的预测效果更好，非限制混频预测模型的均方根误差为自回归模型的70%，平均绝对百分误差率为7.28%，虽然非限制混频模型较多的估计参数影响了其稳定性，但其对我国国民生产总值的预测效果仍然优于其他模型。

参考文献：

1.徐国祥，刘璐.中国消费者信心指数与居民消费价格指数的关系研究[J].统计与决策，2018，34（23）

2.赵菁.消费结构、产业结构与经济增长的关系—来自中国面板数据的实证[J].商业经济研究，2018（22）

3.黄昶生，喻洪仙.国际油价波动对我国消费者信心指数的影响研究—基于VAR模型的实证分析[J].价格理论与实践，2016（5）

4.施颖.消费者的网络消费行为特征与影响因素实证分析[J].商业经济研究，2017（4）

5.李成.消费者信心能预测产出波动吗—来自中国的经验证据[J].经济学动态，2016（12）

6.王岱，程灵沛，祝伟.我国消费者信心的影响因素分析[J].宏观经济研究，2016（4）