一道“游离”模型的中考最值问题

江苏省南京金陵中学河西分校 (邮编：210019)

近几年，笔者陆续加了几个数学解题研究的QQ群，发现数学解题研究出现了一个误区：过度关注试题解法“模型”，刻意强化解题模型识记，数学解题逐渐形成了套“模型”解题，数学解题教学课有被“模型”化的倾向．遗憾的是不少教师还以为找到解题的捷径和提高学生分数的法宝，热于追捧，乐此不彼．长此以往，数学解题的趣味性、思维性必将丧失．中考试题中的把关题如何精雕细琢，使其既能考查学生的数学思维能力，又能避免学生套用模型走捷径，是引导数学解题教学的“风向标”，值得命题者慎思．2019年浙江省台州市数学中考试卷的第16题就是一道“游离”模型、考查能力的好题．

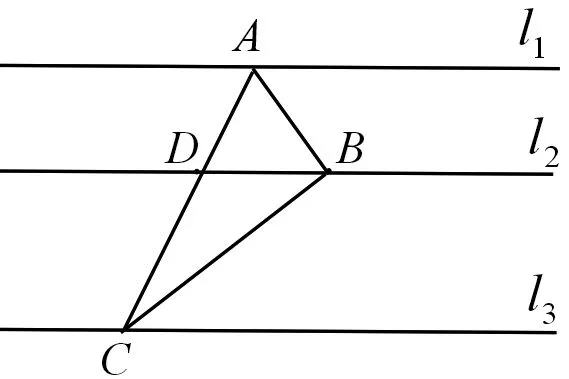
图1

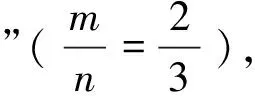
1 由“BD=4且BD∥l1∥l3”联想构造“A”型相似三角形

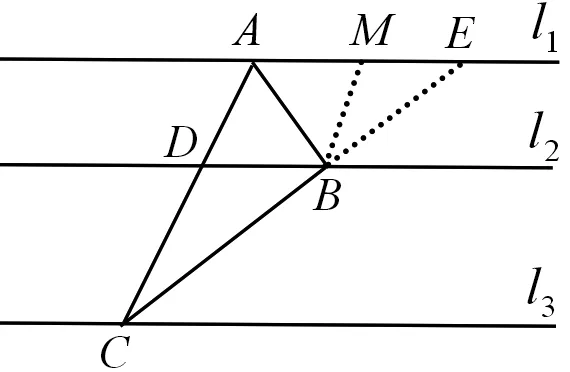
图2

解法1 如图2，延长CB交l1于点E，

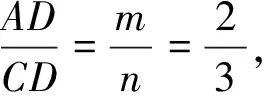
且△CBD∽△CEA，

因为∠ABC=90°，所以∠ABE=90°，

图3

解法2 如图3，延长AB交l3于点E，

取CE中点M，连接BM，以下同解法1(略)．

2 由“BD=4且联想构造“X”型相似三角形

图4

解法3 如图4，作EA⊥AB交l2于点E，

则AE∥BC，所以△AED∽△CBD，

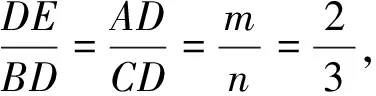
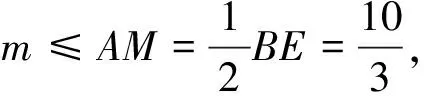
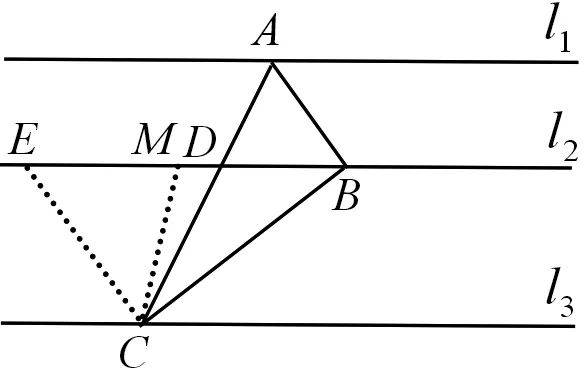
图5

解法4 如图5，作EC⊥CB交l2于点E，

取BE中点M，连接CM，以下同解法3(略)．

评注笔者曾在2017年《中学数学》(初中版)第6期发表“打造中线 破解最值”一文，上述4种解法借助相似三角形求出直角三角形斜边长度后，正是采用的此法．无独有偶的是，2019年深圳中考压轴题的最后一个问题，也是求两条线段之比的最大值，利用此法可直接秒杀，有兴趣的读者不妨一试．

3 由“BD=4且∠ABC=90°”联想构造“K”型相似三角形

图6

解法5 如图6，过点B作EF⊥l2分别交l1、l3于点E、F，

过点D作GH⊥l2分别交l1、l3于点G、H，

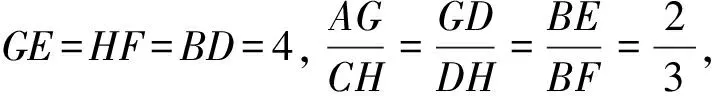
设AG=2x，则CH=3x，

进而AE=4-2x，CF=4+3x，

故n的最大值为5，

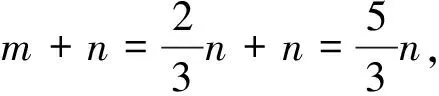
4 由“BD=4且m表示直线l1、l2之间的距离”联想面积法

图7

解法6 如图7，过点D作DE⊥AB交AB于点E，

设AE=2k，则BE=3k，AB=5k，

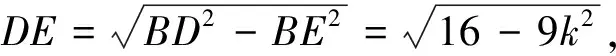
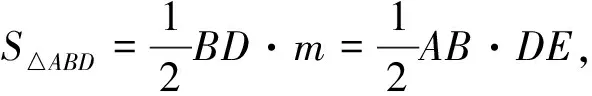
评注与前4种解法不同，解法5、6是从代数的角度构建函数，再利用配方法求解，这也是求解最值问题的自然解法之一．

研究解题过程，不是去寻找万能的解题模式，而是力图揭示人的思维活动过程和解题的有效途径，它重在培养学生独立思考的能力和从数学的角度去分析问题的素养，让学生学会独立思考，体会数学思想和数学思维方式，使学生终身受益；它是数学教师的立足之本，是数学活动的基本形式和主要内容，是师生的一个兴奋中心．模型是一把双刃剑，借助重要的模型来解题无可厚非，但数学教学切不可课堂动辄言谈解题模型，尤其是一些脱离学生实际、不着边际的“模型”．