商榷2019年高考题中表述欠严谨的14道题
2019-10-28北京丰台二中邮编100071
北京丰台二中 (邮编:100071)
一年一度的高考是考生、老师、家长、学校乃至全社会关注的重点话题.2019年的高考已尘埃落定,笔者作为一名高中数学老师,也抓紧时间认真钻研了本年度的高考数学真题(文理共计13套,其中上海、浙江文、理同卷,江苏文、理除附加题外同卷),发现了它们有试题常规(多考计算)、情景新颖、杜绝偏怪等特点,这也与新课改之精神、教育乃培养人的活动、数学本来应当是人人能够喜爱的美的科学合拍.但笔者发现有14道高考题在表述上欠严谨:虽然原题不会太影响考生正确答题,但作为高考题的权威性及引用的广泛性,还是要注意表述上的严谨.
笔者发表的文献[1]-[5]分别对2014~2018年的高考题在表述上欠严谨之处也作了商榷.
1 全国卷I

图1

A.165 cm B.175 cm
C.185 cm D.190cm
流行解法B.头顶至脖子下端的长度为26cm,说明头顶到咽喉的长度小于26cm.
又因为肚脐至足底的长度大于105cm,可得头顶至肚脐的长度大于105×0.618≈65(cm),即该人的身高大于65+105=170(cm).
综上所述,可得身高在170cm-178cm之间.因而选B.
正确解答解答本题必须要得到相应的不等式,不能由近似计算来求解.



再结合选项,可知选B.
商榷“咽喉”指喉咙,包括咽、食管上部、喉及气管的通向胃和肺的通道,颈的前方上部紧接面颊的部分.因而“咽喉”不是一个点,所以题1中的“头顶至咽喉的长度”、“ 咽喉至肚脐的长度”说法均不通.
另外,因为题1运算量较大且涉及的量较多,所以建议把题1放置在试卷中选择题倒数第二题或倒数第一题的位置(因为这份试卷第5~12题都很基础常规,且运算量均不太大).

图2
题2 (2019年高考全国卷I文科第19题与理科第18题的综合表述)如图2,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)(文)求点C到平面C1DE的距离;
(理)求二面角A-MA1-N的正弦值.
商榷现行高中数学教材(比如普通高中课程标准实验教科书《数学2·必修·A版》(人民教育出版社,2007年第3版)(下简称《必修2》))中均没有给出“直四棱柱”的概念(给出了“四棱柱”的概念),因而建议把题2题设中的“直四棱柱ABCD-A1B1C1D1的底面是菱形”改为“四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱A1A与底面垂直”.
题3 (2019年高考全国卷I文科第21题)已知点A,B关于坐标原点O对称,│AB│=4,⊙M过点A,B且与直线x+2=0相切.
(1)若A在直线x+y=0上,求⊙M的半径;
(2)是否存在定点P,使得当A运动时,│MA│-│MP│为定值?并说明理由.
商榷因为现行关于平面解析几何的高中数学教科书(比如《必修2》)中均没有使用过符号“⊙”,所以建议把题3中的第一处“⊙M”改为“圆M(点M是其圆心,下同)”,把题3中的第二处“⊙M”改为“圆M”.
2 全国卷II
题4 (2019年高考全国卷II文科、理科第4题)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日L2点的轨道运行.L2点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,L2点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:

商榷(1)题4以物理知识万有引力定律为背景,突出了数学的应用,宣传了我国航天事业的发展及取得的重大成就.但此题既没有考查物理也没有考查阅读(题目冗长,且第一段文字对解题没有任何帮助,逐字逐句研读完后会大呼上当,会使考生对于应用题不会再看这些无用的文字(又不会排除漏看了有用的信息)的坏习惯,数学考题给出的主要信息应是数学),数学阅读的意义应体现在用数学知识进行等价转化.
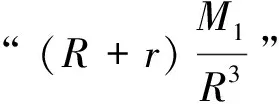
(3)因为题4运算量较大且涉及的字母较多,所以建议把题4放置在试卷中选择题倒数第二题的位置(因为文科试卷第5~11题都很基础常规,且运算量均不太大).

A.f(x)=│cos2x│ B.f(x)=│sin 2x│
C.f(x)=cos│x│ D.f(x)= sin│x│


图3

图4
题6 (2019年高考全国卷II文科、理科第16题)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图3).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图4是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有____个面,其棱长为____.(本题第一空2分,第二空3分.)
商榷建议把该题6中的后四处“半正多面体”均应添上双引号.
题7 (2019年高考全国卷II文科、理科第22题)在极坐标系中,O为极点,点M(ρ0,θ0)(ρ0>0)在曲线C:ρ=4sinθ上,直线l过点A(4,0)且与OM垂直,垂足为P.

(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
商榷建议把题7第(2)问中的“P点”改为“点P”.
因为现行教材中的有关表述均是“点P”,从来没有出现过“P点”,比如《必修2》、普通高中课程标准实验教科书《数学·选修1-1·A版》(人民教育出版社,2007年第2版)及普通高中课程标准实验教科书《数学·选修2-1·A版》(人民教育出版社,2007年第2版)(下简称《选修2-1》).
另外,把“|x|”读作“绝对值x”、“a”读作“a向量”均不对,应分别读作“x的绝对值”、“向量a”.其理由源于教材,比如普通高中课程标准实验教科书《数学4·必修·A版》(人民教育出版社,2007年第2版)中的《第二章 平面向量》.
3 全国卷III
题8 (2019年高考全国卷III文科第12题即理科第11题)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( )
商榷建议把题8中的“为R的偶函数”、“在(0,+∞)单调递减”分别改为“为R上的偶函数”、“在(0,+∞)内单调递减”.

①f(x)在(0,2π)有且仅有3个极大值点
②f(x)在(0,2π)有且仅有2个极小值点
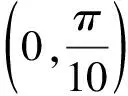
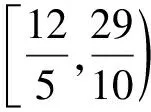
其中所有正确结论的编号是( )
A.①④ B.②③ C.①②③ D.①③④
4 北京卷
题10 (1)(2019年高考北京卷文科第6题)设函数f(x)=cosx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件

A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
商榷(1)建议把这两个小题的前三个选项分别改为“A.充分不必要条件、B.必要而不充分条件、C.充要条件”,这样与《选修2-1》第11页习题1.2A组第3题的答案一致.对于2019年高考天津卷文科第3题及理科第3题,也应有这样的改动.
(2)若把题设“设点A,B,C不共线”去掉,则答案是A.另外,建议把题目中的“点A,B,C不共线”改为“三点A,B,C不共线”.

图5

(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;


题12 (2019年高考北京卷理科第18题)已知抛物线C:x2=-2py经过点(2,-1).
(1)求抛物线C的方程及其准线方程;
(2)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=-1分别交直线OM,ON于点A和点B,求证:以AB为直径的圆经过y轴上的两上定点.
商榷在题12第(2)问的解法中用不到到条件“斜率不为0”,所以把该条件去掉后所得结论仍然成立.事实上,当“直线l的斜率为0”时,可得点M与点A(或点B)重合,其坐标是(-2,-1);点N与点B(或点A)重合,其坐标是(2,-1),进而可求得以AB为直径的圆的方程是x2+(y+1)2=4,它也经过y轴上的两个定点(0,-3)与(0,1).
因而建议去掉第(2)问中的“斜率不为0的”.
5 江苏卷

图6

(1)求椭圆C的标准方程;
(2)求点E的坐标.
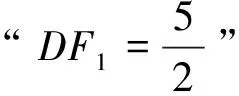
题14 (2019年高考江苏卷第23题)在平面直角坐标系xOy中,设点集An={(0,0),(1,0),(2,0),…,(n,0)},Bn={(0,1),(n,1)},Cn={(0,2),(1,2),(2,2),…,(n,2)},n∈N*.
令Mn=An∪Bn∪Cn.从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
(1)当n=1时,求X的概率分布;
(2)对给定的正整数n(n≥3),求概率P(X≤n)(用n表示).
商榷建议把题中的“求X的概率分布”改为“求X的概率分布列”,因为在普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社2009年第3版)的“第二章 随机变量及其分布”中表述的都是“求X的概率分布列”.
关于2019年高考天津卷(文、理)、上海卷、浙江卷,笔者没有发现值得商榷之处.
