初中数学中的最值问题模型构造和应用策略研究

谢承敏.广西凌云县民族初级中学.广西百色.533199

一、初中数学中模型思想的应用方式

模型思想指的是使用数学模型方法有效解决以及处理实际问题的思想，其是学生理解以及体会数学和现实联系的重要桥梁，构建和求解模型的过程包含了从具体情境或者是现实生活当中抽象数学问题，使用数学符号有效的构建不等式、方程以及函数等数学问题当中的数量关系以及变化规律，最终获得结果，并且探究结果意义。学习数学模型思想可以有效的提升学生数学学习的兴趣，加强应用意识，最终完成建模的有效策略。

最值问题作为初中数学的关键性内容，同时也是中考中经常会涉及到的热点性问题，是一类综合性相对较强的问题，考察学生利用所学知识有效解决实际问题的根本能力。不管是代数亦或是平面几何，学习中都会碰到最值问题，常见的便是线段以及最值问题，这类题目通常可以归为两种形式：第一，几何模型，多是在存在不确定位置关系以及动点的时候求最值，该类问题的解答通常由两种方法，一种是通过几何图形性质确定位置。第二，函数模型，经常按照已知的条件，将问题逐渐演变为两个变量的关系，从而构造二次函数的解析式，利用配方使用二次函数增减性与对称性，最终明确某个特定范围内函数最大、最小值。

二、模型的构造

教学是从简单到复杂，从特殊到一般的过程，为了能够让学生顺利的开展学习工作，笔者选取了2个动点以及1个定点间距离相等，同时2条线段形成夹角是直角这个特殊的情况引入。

如图1所示，已知A（0，5），B点是x轴的一点，在A点上做CA⊥AB，同时CA=AB，如果B点沿着x轴运动，C点随之运动，那么OC最小值是？

在做这个题目的时候，教师要让学生认真的观察各个点的运动情况，然后回答以下问题。

第一，我们要探究的是哪个动点的实际运动轨迹？

学生都能够回答是C点。为了能够贯彻新课程改革中以学生为教学主体的要求，在实践教学工作中，可以让学生四人作为一个小组进行集中讨论，并且用画图的形式探究以及观察，猜想B点沿着x轴运动的时候，C点的运动轨迹。通过对图形的观察，学生可以猜想出C点的运动轨迹为直线，可是无法用数学语言给出证明。为了有效的解决这个问题，教师可以为学生设置相应的问题，引导学生确定C点运动轨迹。

第二，B点运动的时候，图中哪些量是保持不变的？

这个问题看上去非常简单，但是能够帮助学生理清题意，使得学生能够从动中发现静的一面，找出动点运动的进程中所产生的不变量，从而将不变量作为根本出发点，寻找问题解决的方法。

尽管C点、B点都在运动，可是AB与AC是垂直、相等的，也就是AB与AC长度相等，同时∠BAC为90°。教师要引导学生发现这几个不变量。

第三，是否能够将CA⊥AB转变成∠BAC=90°，将CA=AB转变为AB/AC=1的样式？

学生回答可以。此时我们就可以得出模型，

模型：已知A点是定点，B、C两点是动点，同时满足∠BAC=90°，AB/AC=1，如果点B在直线m上运动，那么点C的运动轨迹也是一条直线。通过特殊到一般性的推理，∠BAC并非局限在90°，可以为（0°，180°）区间内的任意角度。

三、模型的应用

下图为一个等边三角形，其边长均为6，E为对称轴AD上的动点，连接EC，线段EC绕着C点逆时针旋转60°获得FC，将DF连接起来，那么在E点运动的进程中，DF最小值为？

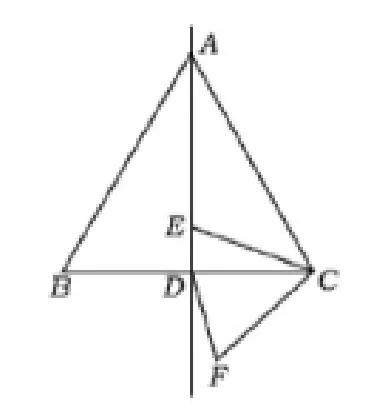
图1

图2

点C为定点，E、F两点为动点，∠ECF=60°，同时CE/CF=1，满足模型所规定的条件，所以我们可以明确F运动轨迹为直线，为了确定直线，只需要找到直线上的一个特殊点，E为AD上的动点，为了保持∠ECF不变，F也会运动，在E到达A点的时候，点F正好能够运动到B点，连接BF，即为F的运动轨迹，直线明确以后就能够使用垂线段最短来确定DF最小值，按照模型可以明确∠EGB=∠ECF=60°，DF为3/2.

结语

总而言之，最值问题看上去困难、复杂，但是其中包含了一定的模型思想，解决这类题型的时候，关键在于充分的结合题目的意思，利用相应的图形性质以及概念，利用一定的手段与方法，将函数以及几何的最值问题直接转变为基本模型加以解决。教师要从学生的实际情况出发，设置相应的问题引导学生构建模型，并使用模型解决相关题型，引导学生在求解数学模型的进程中，不断的积累各种数学活动经验，构建数学模型思想，有效的提高问题解决能力。