牧马河流域年径流变化特征分析

夏焕清，霍秀秀，曹苗苗

（陕西省汉中水文水资源勘测局，陕西 汉中 732000）

1 研究区概况与数据来源

1.1 研究区概况

牧马河为汉江干流一级支流，源于城固、南郑、西乡3县交界处米仓山北麓的白熊山老鹰崖，流域位于大巴山北部，山地高在2500 m～3000 m之间，大致东向流经城固县、西乡县，在西乡城南三花石乡回龙湾汇入汉江。西乡水文站是牧马河重要控制站，集水面积1224 km2，多年平均降雨量为877.8 mm，7月～9月降水量占全年的50%以上，多年平均径流量为9.04亿m3。

1.2 数据来源及研究方法

采用的径流量数据为西乡水文站(1974年～2018年)的年径流量数据，见表1。

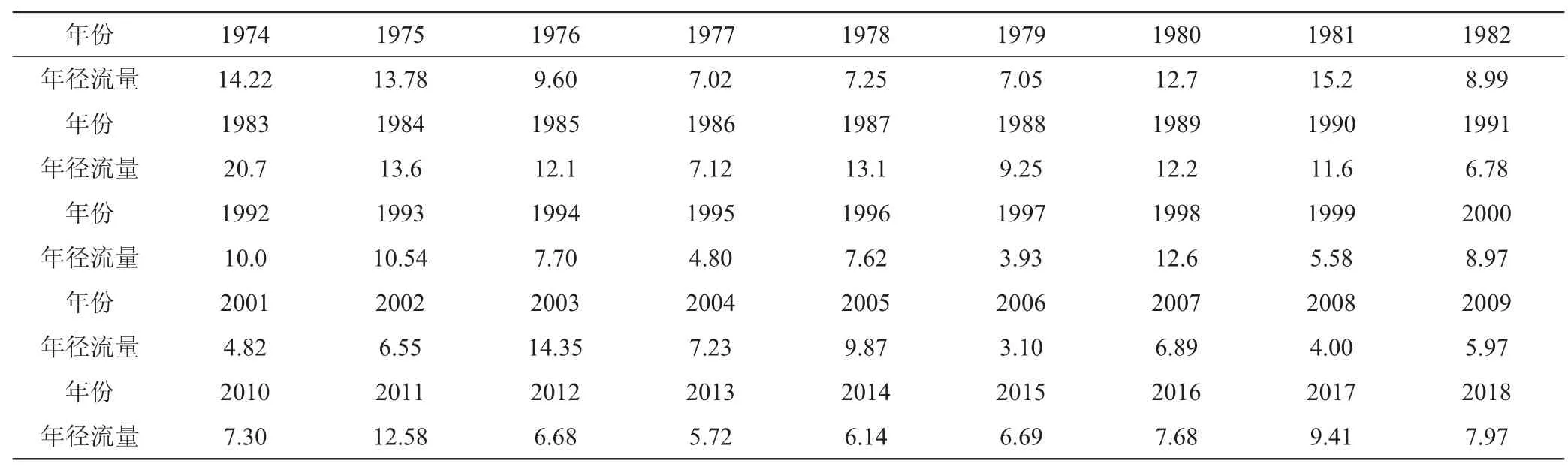
表1 西乡水文站(1974年～2018年)的年径流量数据 单位：亿m3

研究方法为：采用线性回归、五年滑动平均对牧马河流域径流变化趋势进行分析，M-K检验、小波分析分别进行年径流量突变检验与周期分析。数据处理工具：小波分析和M-K检验用Matlab，显著性检验用皮尔逊相关性分析。

1.3 研究方法

1.3.1 线性回归

通过建立牧马河流域西乡站年径流与时间序列之间的线性回归方程，通过回归方程的斜率以及变化趋势的显著程度从而判断因变量趋势变化的方法，表达式：

式中：Xt为t时刻年径流值；t为时间；b为方程截距；a为回归方程斜率。

用10 a表示研究对象时间序列趋势变化程度，当a＞0时，表明年径流具有上升趋势；当a＜0时，具有下降趋势。此外，通过皮尔逊相关分析法来判断年径流变化趋势是否显著，当p＜0.05时，年径流在时间序列上具有显著性上升或下降趋势；当p＞0.05时，年径流不具有显著变化趋势，本文通过SPSS17.0对年径流变化趋势进行显著性检验。

1.3.2 滑动平均

滑动平均是可以直观反映年径流时间序列变化趋势的一种方法，通过计算西乡站年径流系列（1974年～2018年）44年径流项连续5项序列的平均值。从第1项至5项的算术平均为滑动平均第1项，最后1项是原来44年径流序列的第40至第44项的算术平均。若西乡站年径流序列具有趋势成分，则5年滑动平均能够将西乡站年径流的趋势直观的显示出来。

1.3.3 Mann-Kendall突变检验

对于西乡站年径流样本时间序列 X1、X2、X3、X4…Xn，mi表示第i个样本Xi大于Xj（1≤j≤i）的累计数，则构造统计量：

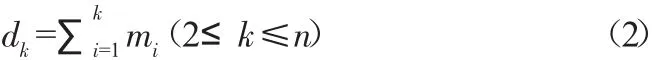
在序列相互独立的假设条件下，的均值和方差为：

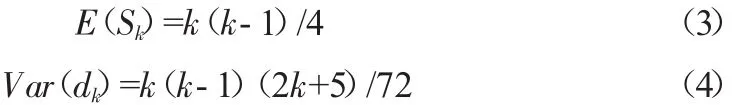
将公式标准化得到以下计算式：

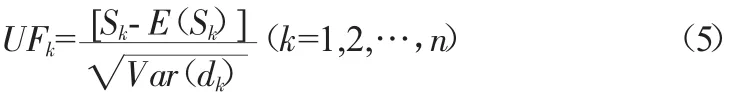
UFk计算结果组成UF曲线，同样以此方法引用到反序列中，计算得到 UBk，使得 UBk=-UFk。

给定显著性水平0.05，统计量临界值±1.96。通过绘制UFk、曲线图UBk，如果两条曲线在置信度0.05水平内相交，则定义为突变点。如果UFk或UBk的值大于0，则表明序列具有上升趋势，反之，序列呈下降趋势。当曲线超出置信度区间时，表明序列具有显著的上升或下降趋势，该过程通过Matlab工具调用编辑的西乡站年径流M-K突变检验程序，来实现相关过程计算及作图。

1.3.4 小波分析

小波分析方法是一种在空间固定的基础上反映时频局部发生变化的分析方法。基本原理用一簇小波函数系来表示或逼近某一信号或函数。小波分析最关键的部分是小波函数，小波函数φ（t）∈L2（R），且有：

φ（t）为基小波函数，它可通过尺度的伸缩和时间轴上的平移构成一簇函数系：

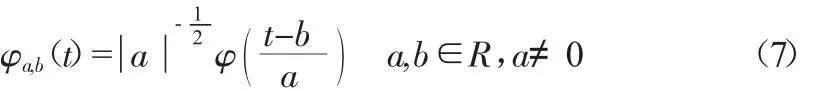
式中：φa,b（t）为子小波；a为尺度因子，反映小波的周期长度；b为平移因子，反应时间上的平移。

对西乡站年径流的研究选用的是Morlet小波函数，其表达式为：

式中：ω0为常数（ω0≥5）；i为虚数。

对于任意函数f（X），其小波变换可以定义为：

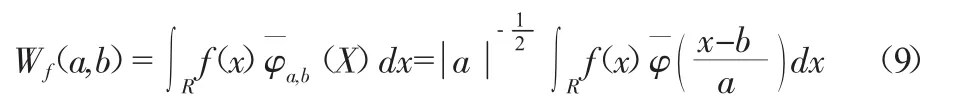
牧马河流域西乡站年径流周期分析计算与出图过程，通过Matlab工具调用编辑的西乡站年径流周期分析程序来实现小波分析。

3 结果与分析

3.1 趋势分析

图1中圆点折现图为年径流量图，三角折线图为五年滑动平均图，方程式为年径流量图趋势线方程式。由图可知，年径流趋势线k为-0.1505，即年径流量趋势为减小；利用皮尔逊相关性分析，在显著性水平为0.01以下，皮尔逊相关性系数为-0.459，两个变量为负相关且显著相关；五年平均滑动图趋势线k为-0.1346，五年平均径流量趋势为减小。

图1 年径流及五年滑动平均图

3.2 突变分析

图2 UF小于0表明呈下降趋势，当UF和UB两条曲线出现交点，且交点在临界直线之间，交点对应的时间即为突变开始时刻。从图2可知，西乡站年径流量突变时间为1990年。

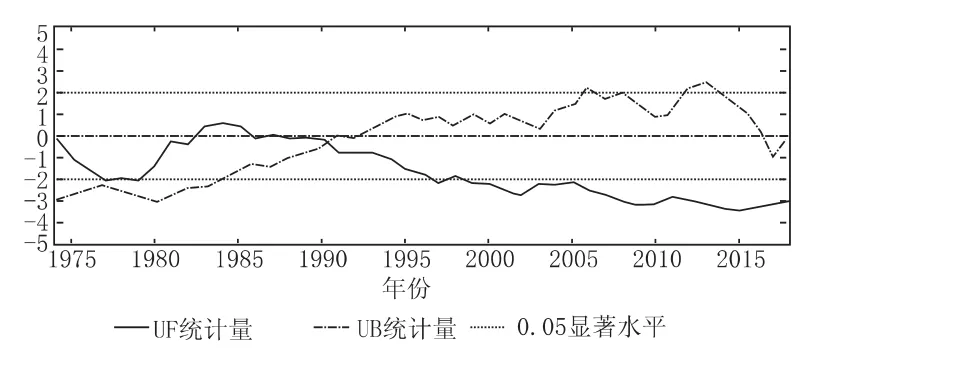
图2 M-K突变检验图

3.3 周期风险

在不同的时间尺度下，年径流量的变化有周期性和时间域上丰、枯变化的特性。

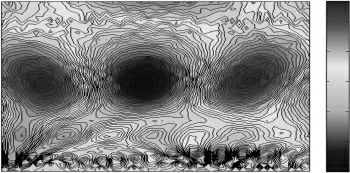
图3 牧马河流域年径流小波系数模方图

图3 为小波模方图，由图3来分析年径流在小波变化域中波动能量大小的变化特性，进而反映哪些能量聚集中心主导年径流在时间域上的波动变化的情形，分析可知，在5 a、10 a、23 a左右的时间尺度上能量聚集中心闭合较好并且分布密集，与图5比较没有30 a以上的，原因为时间序列尺度不够长。

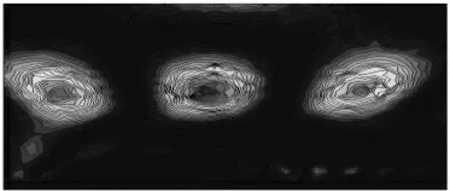
图4 牧马河流域年径流小波变换实部图

图4 为小波系数实部的时频分布图，表示年径流在小波变化域中以基准面上下起伏的波动情况，从而反映年径流在时间尺度上丰、枯变化的特性，依图可知西乡站年径流丰枯变换情况，丰水年在1980年、1989年、2011年左右，枯水年在1986年、2001年左右。

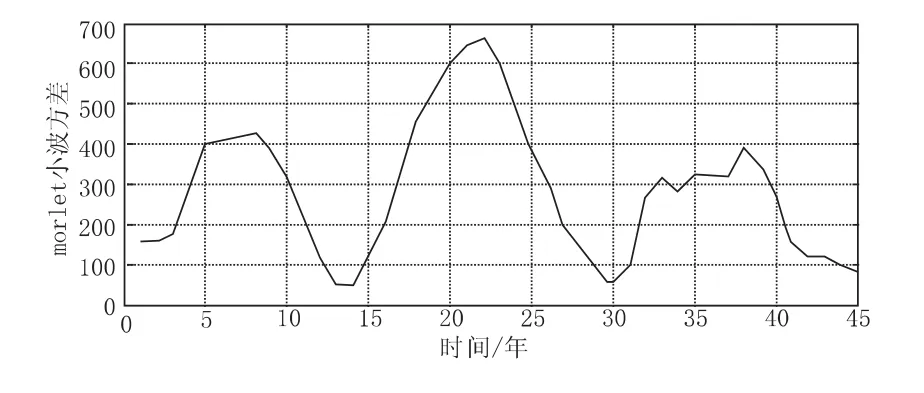
图5 牧马河流域年径流小波变化方差图

由图5可知，小波方差在8 a、22 a、38 a左右的时间尺度上存在峰值，22 a左右的周期震荡最强，是流域的第一主周期，第二、三周期依次约为8 a、38 a，由于西乡水文站建站时间较短，年径流数据序列较短，因此无法准确预测更长时间尺度的周期。

总体来看，西乡水文站年径流周期为22 a～23 a，三个丰水年之间的间隔为 9 a、22 a、31 a 与图 5 分析的周期 8 a、22 a、38 a左右，契合度较高。但在长周期上有较大差别，分析主要原因是随着时间序列的增加，小时间尺度上的突变点逐渐退化为非突变点，随着时间尺度的降低，突变点增多，大时间尺度上的一些平常态，在低层次上转化为突变态，而本文因时间序列较短，在长周期上判断不够准确，进一步说明年径流周期随时间尺度的不同而变化。

4 结论

采用采用线性回归、滑动平均法、MK检验、皮尔逊相关分析和小波分析方法分析牧马河西乡水文站天然年径流时间序列进行多时间尺度变化特性的分析。结果显示:西乡水文站的年径流呈减小趋势，年径流突变时间为1990年左右，呈周期性变化，主周期为22 a～23 a左右，它主导着牧马河年径流长期变化的特性，同时也存在着8 a～10 a、38 a左右的较强周期变化。在1980年、1989年、2011年左右为丰水年，在1986年、2001年左右为枯水年。