趾板型式对面板堆石坝变形特征的影响
2019-10-25梁锦华费文平
梁锦华,费文平
(1.广东省水利水电第三工程局有限公司,广东 东莞 523710;2.四川大学水利水电学院,四川 成都 610065;3.四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065)
0 引言
在混凝土面板堆石坝中,趾板是大坝面板防渗体系与地基防渗体系的连接构件,通过设有止水的周边缝与面板连为一体,其主要作用是防渗。同时趾板也是基础灌浆的盖板和面板的基座。因此,趾板的变形特征直接影响大混凝土面板堆石坝的运行安全。
通常情况下,趾板设计成与面板正交布置,以避免产生应力集中现象。但有时为了施工方便或减少两岸边坡开挖量,趾板与面板只是在河床部位正交,两岸部位的趾板则与面板保持在同一平面,成非正交接触,这样在自重及水荷载作用下有可能导致趾板与面板相互挤压或大幅度错动,从而产生不利的应力变形状态,严重时会导致面板的压碎或拉裂。
在堆石材料的模型研究方面,邓肯-张E-B模型因其物理概念清晰、计算简单、模型参数少且均可由常规三轴试验测定,成为面板堆石坝有限元分析采用较多的一种本构模型,不少学者借用大型商用软件开展邓肯-张E-B模型的二次开发。
尽管前人对堆石料的材料模型展开的大量的研究工作,但对趾板的结构型式,特别是与面板非正交的布置方式对趾板和面板应力变形的影响的研究尚未见报道。四川省某水库坝高近百米,施工时趾板与面板采用非正交的布置方式,结构型式特殊,砼面板坝、趾板及周边缝受力条件复杂。本文利用ANSYS二次开发出的邓肯-张E-B模型,对砼面板坝进行三维非线性有限元分析,分析接触部位的应力分布规律及周边缝的三向变位情况,评价趾板和面板非正交接触方式对面板和趾板安全稳定性的影响。
2 面板堆石坝的本构模型
2.1 堆石体的本构模型
为充分考虑土体的非线性变形特征,目前普遍采用非线性弹性的邓肯—张本构模型来模拟堆石体的应力应变关系,包括E-v模型和E-B模型。邓肯—张模型的主要优点是可以利用常规三轴固结排水剪切试验确定模型参数。1980年,邓肯等人对E-v模型进行了修正,采用切线体积模量代替切线泊松比进行计算,即为E-B模型。邓肯—张E-B模型的切线杨氏模量和体积模量可表示为:
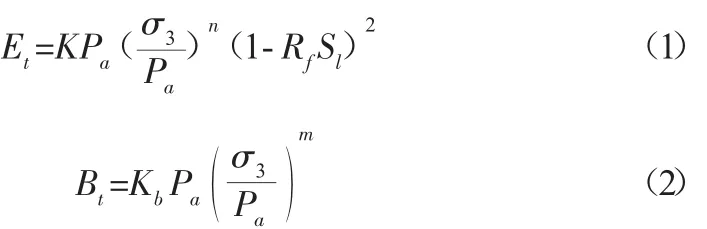
式中:K为杨氏模量系数,Pa为大气压,n为切线杨氏模量Et随围压 σ3变化的幂次,Rf为破坏比为应力水平,c、φ为粘聚力和内摩擦角;Kb为体积模量系数,m为体积模量Bt随围压σ3变化的幂次。
对于卸载情况,该模型采用回弹模量Eur进行计算,回弹模量的表达式如下:
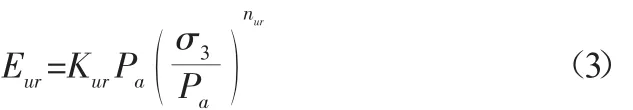
式中:Kur为卸载模量基数,nur为卸载模量指数,且一般情况下nur≈n。
由于堆石体的强度包线有弯曲而呈非线形,需对内摩擦角φ进行修正:

式中:φ0为σ3=Pa时的φ值;Δφ反映φ值是随σ3而降低的一个参数。
2.2 混凝土面板及地基的本构模型
混凝面板及地基采用线弹性本构模型,其应力应变关系符合广义虎克定律:

式中:[D]为弹性矩阵,表达式为:
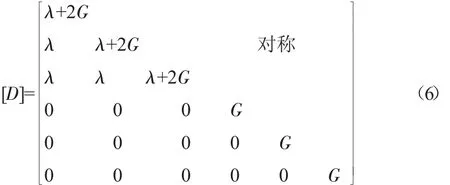
式中:λ为拉梅系数,G为剪切模量,与弹性模量E和弹性泊松比v有关。
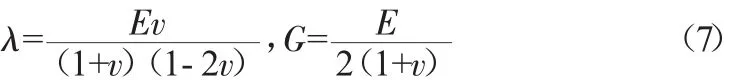
2.3 接触面模型
面板堆石坝面板的分缝及周边缝采用库伦摩擦本构模型,来模拟其相对滑移或张开现象。
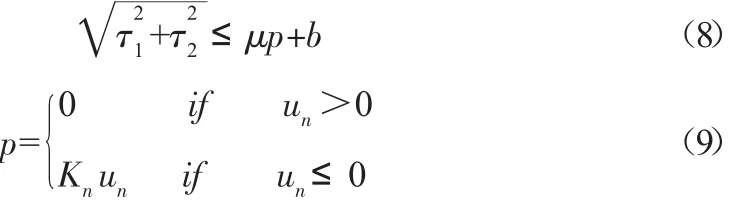
式中:τ1、τ2分别为接触面两个方面的剪应力;μ为接触面的摩擦系数;p为接触面的法向压力;b为接触面粘聚力;un为接触面张开度;Kn=αEh为接触面法向刚度,α为法向接触刚度系数,E为接触面两侧砼的弹模,h为接触单元的平均尺寸。
3 三维有限元模型
3.1 工程概况
某混凝土面板堆石坝坝顶高程1823 m,坝前正常蓄水位1820 m,设计洪水位1820.18 m,校核洪水位1821.22 m,坝顶轴线长370 m,坝顶宽8 m,趾板建基面高程1734 m,最大坝高89 m。上游坝坡1∶1.5,下游坝坡1∶1.6并设二级3.0 m宽的马道。坝面采用30 cm~60 cm厚的C30钢筋砼面板,面板在河床中心线附近设置了14条压性垂直缝,左右坝段设置了15条张性垂直缝,缝内设铜片止水和橡胶止水带,缝内GB填料嵌缝。
趾板为C30钢筋砼水平型趾板,沿河床和岸坡布置。趾板采用了2种形式:第一种是1780 m以下部位趾板宽度6.5 m,厚度1.0 m;第二种是1780 m以上趾板宽度4 m,厚度0.6 m;两岸坝肩趾板大部分置于强风化基岩上部,为加固趾板与基础间连接,在趾板下设置了Φ25锚杆,锚杆长6 m,布置在固结灌浆孔上。趾板和面板间设周边缝,缝内设铜片止水。
在该工程趾板的施工过程中,为减少开挖工作量及施工方便,周边趾板面与面板表面处于同一平面,岸边趾板段的周边缝缝面为铅直缝,导致趾板侧面与面板侧面不正交。本文对比研究两种型式的趾板,分析其对大坝结构的影响。
型式一(实际情况):岸边趾板面与面板表面处于同一平面,岸边趾板段的周边缝缝面为铅直缝;
型式二(通常情况):岸边趾板面与面板表面法向正交接触,周边缝缝面垂直于面板表面。
3.2 计算模型
计算坐标系原点取在堆石坝防浪墙上游侧,X方向为沿水流方向从上游指向下游为正,以上游边墙处为零点,Y方向为铅直向上方向,以海拔零高程为零点,Z方向垂直于水流方向,由右手螺旋法则确定。有限元模型见图1,混凝土面板和趾板为C30,材料参数见表1,堆石区的E-B材料参数见表2。根据工程经验,面板分缝及周边缝的摩擦系数取0.5,粘聚力取0.01MPa,法向刚度系数取0.5。

表1 混凝土材料参数

表2 E-B模型参数
图1 堆石坝整体结构的三维有限元计算网格图
4 趾板型式对面板堆石坝的影响分析
本文通过完建工况、正常工况、设计工况、校核工况这四种工况对两种趾板型式进行分析。
4.1 堆石坝位移对比分析
两种趾板型式的最大位移对比见表3。以位移最大的校核工况为例(位移等值云图见图2~图4),分析两种趾板结构型式下坝体结构的变形特性。由表3和图2~图4可以看出:①堆石坝以顺河向和竖向位移为主,且位移量值均较小。顺流向位移以向下游为主,横流向位移以从两岸向河床为主,竖向位移以竖直向下为主;②堆石坝顺流向最大位移为75.5223 cm,发生在下游中下部部位,方向向下游;竖向最大位移为42.8901 cm,发生在坝体中上部,方向竖直向下;横流向最大位移为30.8945cm,发生在下游中下部,方向从两岸向河床。
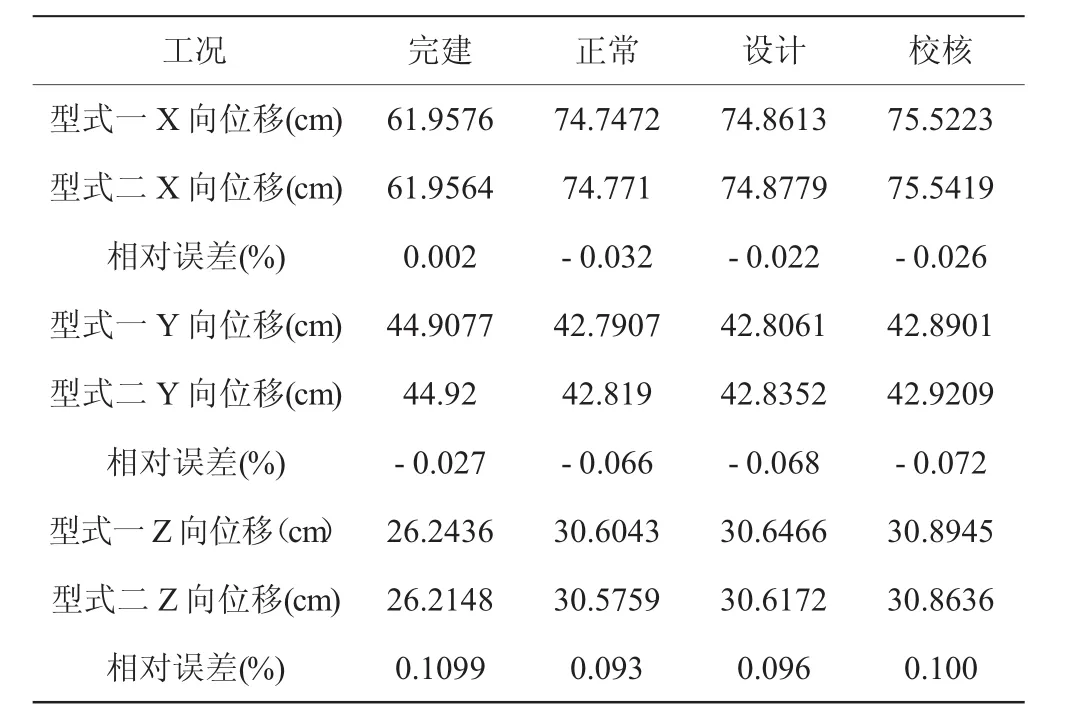
表3 各工况下堆石坝位移
由表3可知:两种趾板计算所得的位移值相差较小,最大相对误差仅为0.1%左右,这是因为两种趾板结构型式只是在延伸方向的改变,加上地基的约束作用,并未引起明显的位移改变。

图2 校核工况下堆石坝X方向位移等值云图(m)
图3 校核工况下堆石坝Y方向位移等值云图(m)
图4 校核工况下堆石坝Z方向位移等值云图(m)
4.2 周边缝最大错动位移对比分析
周边缝两种趾板型式的最大错动位移的对比见表4。
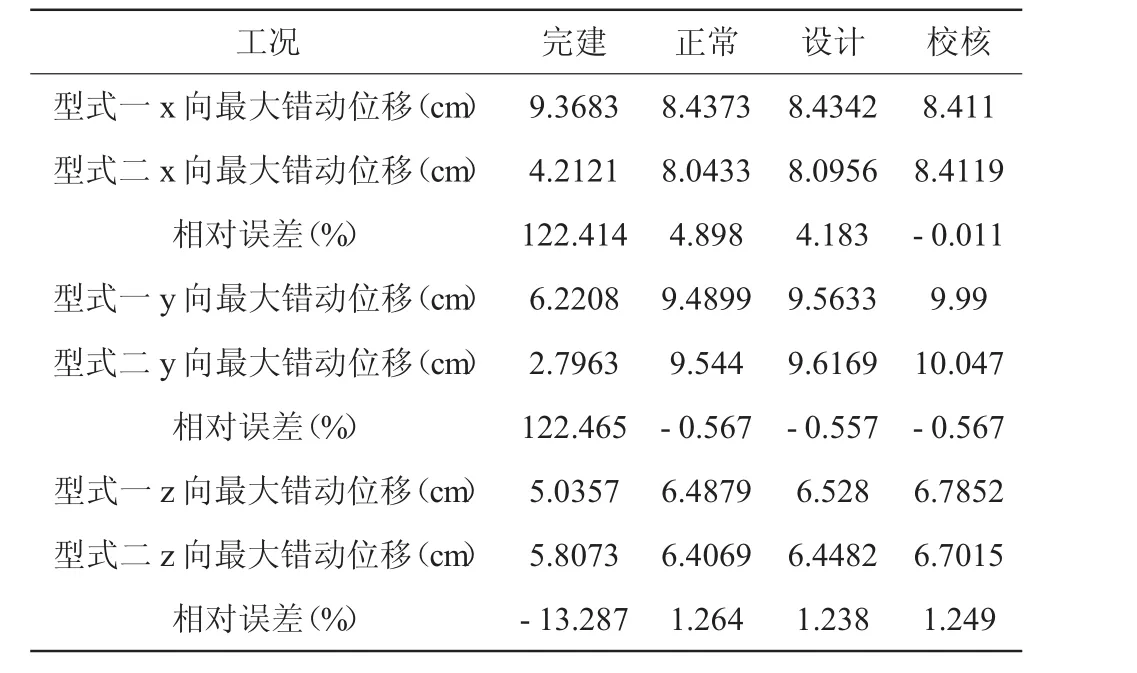
表4 各工况下周边缝最大错动位移
由表4可以看出,在正常、设计、校核工况下,两种趾板布置型式的周边缝错对位移相差不大,但在完建工况,相差较大。相比较而言,型式一在x和y方向周边缝的相对错对位移更大,对结构的变形不利,在z方向的相应位移两者相差不大,因此型式二更优。但整体错对位移仍在周边缝及止水可变形的范围之内,不影响结构的安全。
4.3 趾板应力的对比分析
趾板在两种趾板型式的最大应力的对比见表5。
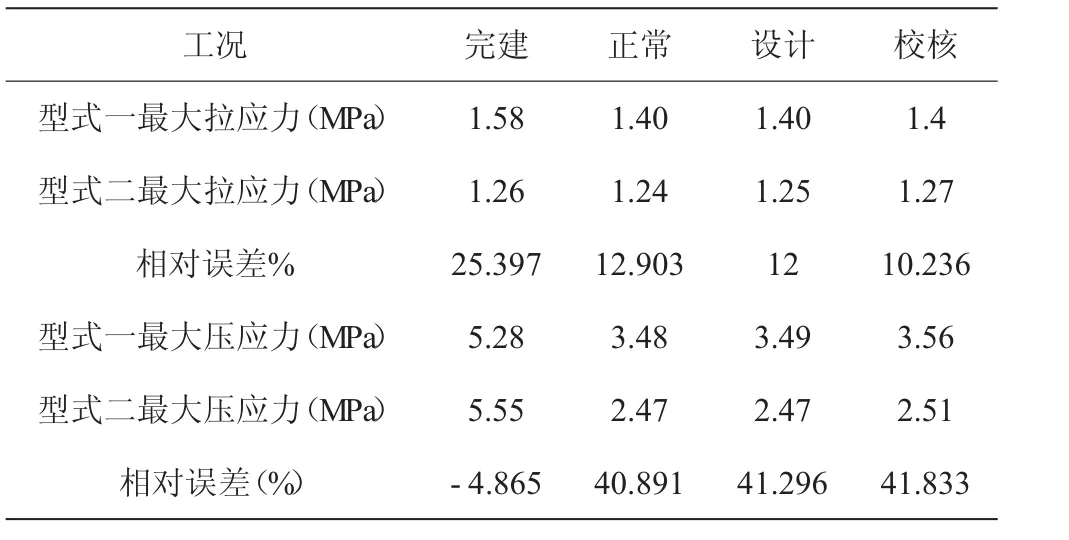
表5 各工况下趾板的最大应力
以对应力最不利的完建工况为例,从第一主应力和第三主应力的云图图5~图6可知:①型式一,趾板的最大拉应力为1.58 MPa,发生在左岸变厚度处,最大压应力为-5.28 MPa,发生在上游坝脚,最大剪应力为-2.12 MPa,发生在左岸变厚度处。②型式二,趾板的最大拉应力为1.26 MPa,发生在左岸变厚度处,最大压应力为-5.55 MPa,发生在左岸坝脚,最大剪应力为-2.34 MPa,发生在左岸变厚度处。③在趾板各变截面处均出现了应力集中现象。④趾板的布置型式对最大拉应力和最大压应力均会产生一定的影响。型式一由于采用了非正交的斜向布置型式,趾板的受力条件不如型式二所采用的法向布置型式,会导致拉应力的增大,甚至超过了C30砼的抗拉强度1.43 MPa,需由钢筋承担部分拉应力。两种型的最大抗压强度均小于C30砼的抗压强度。因此,从应力状态来看,型式二更优。
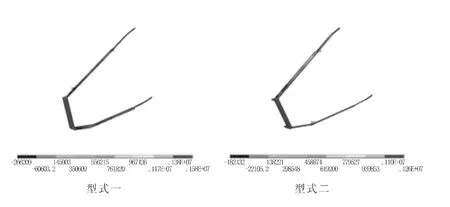
图5 完建工况下趾板σ1等值云图(Pa)

图6 完建工况下趾板σ3等值云图(Pa)
5 结论
本文基于ANSYS二次开发的堆石体E-B模型,采用三维非线性有限元法分析了两种趾板型式在各工况下的应力应变及周边缝错动情况,主要结论如下:
(1)两种趾板型式下,堆石坝的位移值在各工况下相差较小。
(2)两种趾板型式下,各工况下周边缝的错对位移相差较大,在完建工况下相差122.465%。
(3)两种趾板型式下,各工况下趾板的应力值相差较大,在完建工况下最大拉应力相差25.397%。
(4)现状趾板与规范趾板相比,周边缝的错对位移及趾板的应力水平都有较大幅度的提高,但位移值和应力值仍在结构允许范围之内,结构可满足安全运行要求。
(5)对非正交的趾板布置型式在工程中应谨慎采用,如需采用要进行相关论证。
