不同侧风工况下汽车稳定性双向耦合研究

2019-10-25李舒雅谷正气黄泰明郑乐典

中国机械工程 2019年19期

李舒雅谷正气,2 黄泰明刘俊郑乐典

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.湖南文理学院,常德,415000 3.湖南理工学院机械工程学院,岳阳,414006

0 引言

随着新能源汽车的快速发展，汽车的轻量化程度不断提高，气动阻力不断减小。然而，当汽车更轻、阻力更小时，其侧风稳定性也会更差，进而影响汽车和驾驶员的安全[1]，因此侧风稳定性研究十分重要。

由于汽车的运动姿态变化会影响汽车周围流场的瞬时变化[2-4]，而瞬时变化的流场也会反过来影响汽车的运动姿态[5-6]，因此汽车的运动和流场变化是实时耦合的。目前对汽车在侧风作用下的稳定性研究主要采用多自由度汽车动力学模型与空气动力学模型相耦合的方法[7-9]，以及将风洞试验结果或流场分析结果单向传递给汽车动力学模型进行求解的方法[10-12]。第一种方法对汽车结构进行简化，不能反映汽车细节结构对汽车稳定性的影响，而第二种方法忽略了汽车在流场中的运动变化对气动力的影响，因此这两种方法都不能完全反映汽车在侧风下的运动状态。此外，目前在汽车侧风稳定性的评价中，主要采用类似ISO12021中汽车穿过侧风区的方式模拟汽车受到的环境侧风[7-8]，而汽车在高速路上行驶时，会更多地遇到自然侧风的工况。自然侧风作用于整个汽车，对汽车的稳定性会产生较大影响。

本文结合两种方法的优势，基于能反映汽车实际结构的多体动力学方法(multi body dynamics, MBD)[13-14]和能反映汽车实际瞬态流场特性的大涡模拟(large eddy simulation, LES)方法[7,15]，提出了一种汽车运动与汽车流场实时同步的双向耦合分析方法。

1 数值计算方法

汽车空气动力学仿真和汽车多体系统动力学仿真的耦合分析系统见图1，侧风对汽车的影响通过计算流体动力学(computational fluid dynamics, CFD)模型引入，路面和驾驶员对汽车的影响通过MBD模型引入。同时，CFD模型将侧风作用下的汽车气动力通过耦合平台传递给MBD模型进行计算，而MBD模型在气动力、路面和驾驶员的综合作用下，将运动反馈给汽车CFD模型，以此实现汽车流场变化和汽车运动变化的实时耦合。

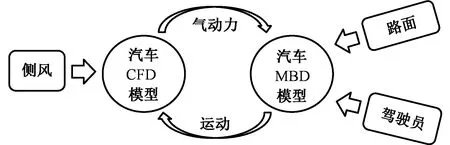
图1 CFD与MBD双向耦合分析系统Fig.1 Two-way coupling system of CFD with MBD

本文数值仿真计算采用某汽车1∶1模型(图2)。车长4.587 m、宽1.799 m、高1.467 m。当车速为100 km/h时，基于车长的雷诺数为8.7×106，因此汽车周围为高雷诺数湍流流场；同时由于汽车车速低、马赫数小，因此汽车周围流场通常被看作不可压流场。

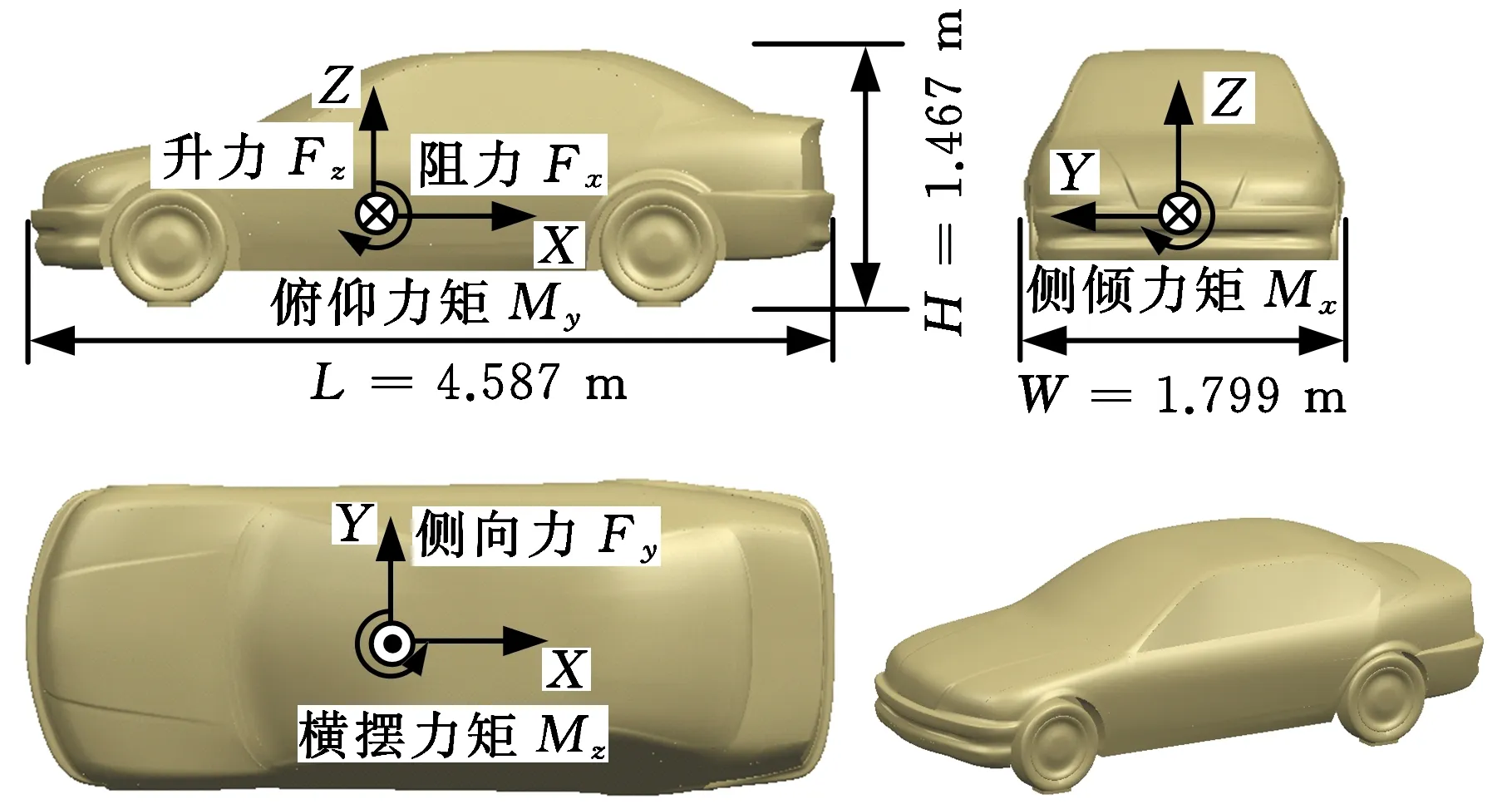
图2 汽车模型和坐标系Fig.2 Vehicle model and coordinate system

坐标系设置见图2，坐标原点为该汽车的质心位置，汽车前进方向为X轴负方向，汽车驾驶员右侧为Y轴正向。为避免坐标系转换过程中产生数据误差，仿真中气动力的获取和运动的交换以全局坐标系作为参考。

1.1 数值计算管理方程

1.1.1空气动力学数值方法

汽车瞬态流场的计算采用LES方法。LES方法中，流场的湍流流动是由不同尺度的涡组成的，其中大型的涡采用直接数值模拟(direct numerical simulation, DNS)方法求解N-S(Navier-Stokes)方程，而对于小型的涡，通过滤波函数过滤之后，利用亚格子模型将小型涡对大涡的影响考虑进去，相较于DNS，LES法既缩短了计算时间，又降低了计算资源要求，同时相较于传统的湍流模型模型，还提高了计算精度。

经滤波后的基于LES法的非定常不可压N-S方程可以表示为

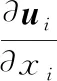
(1)

(2)

(3)

(4)

式中，ui、uj为速度矢量；p为压力；ρ为空气密度；ν为空气的运动黏度；νSGS为亚格子尺度涡黏度；Sij为求解尺度下的应变率张量分量。

本文采用标准Smagorisky模型，式(2)中的亚格子尺度涡黏度νSGS可以描述为

(5)

(6)

式中，cs为Smagorisky模型常数，本文取cs= 0.1[16-17];Δ为网格过滤尺度，可以定义为每个单元体积的立方根；fd为van Direst阻尼方程；y+为距离表面法向的量纲一长度。

1.1.2多体动力学数值计算方程

本文的汽车动力学模型采用多体动力学虚拟样机模型，采用第一类拉格朗日方程描述各个构件的运动。汽车由若干的构件和约束组成，其中每个构件和约束方程基于全局坐标系可以表示为

(7)

式中，q为广义坐标变量，由沿三个方向的位置和三个角度组成，即qT=(x，y，z，ψ，θ，φ)，其中角度的旋转采用3-1-3规则；K为该构件的动能；Fq为作用力矩阵；Ck为某个约束副里的第k个约束方程；λk为拉格朗日乘子数组，共有m个作用在该构件上。

将每个构件和运动副的约束方程组合，得到汽车多体系统动力学管理方程：

(8)

式中，Φq为约束方程矩阵。

以上微分-代数方程(differential-algebraic equations, DAE)采用GSTIFF积分器求解[18]，得到各个构件上的运动和作用力。

1.2 空气动力学计算模型

采用图3所示的计算域进行空气动力学计算。其中L为汽车车长，汽车模型距计算域前部入口3倍车长，距尾部出口7倍车长。W为汽车车宽，汽车距左侧入口4倍车宽，距右侧出口10倍车宽，经计算，计算域的设置满足阻塞比的要求[19]。计算域前侧和左侧均为速度入口，纵向速度为100 km/h；后侧和右侧为压力出口，大小为大气压；汽车车身为无滑移壁面，计算域底部和顶部为滑移壁面。

图3 计算域设定Fig.3 The setup of the fluid domain

汽车在流场中的运动姿态变化由Arbitrary Lagrange-Euler(ALE)动网格方法实现[7]。在本文的CFD仿真中，汽车的运动参数来源于多体动力学模型的计算结果，流场中的汽车得到运动参数后，汽车车身在5个自由度方向产生运动(车身前进方向的自由度用相对风速处理，因此去除了X轴方向的自由度)，汽车周围的网格在Smoothing和Remesh方法下进行变形和重构。采用商业软件ICEM CFD在汽车周围生成四面体非结构网格，为了满足大涡模拟的壁面网格要求，将车身表面网格拉伸出平行的边界层棱柱网格[20]，划分完成网格见图4。

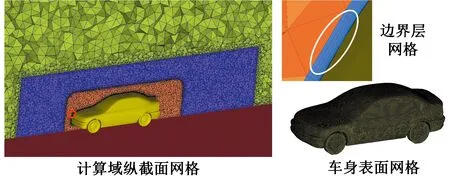
图4 计算网格Fig.4 The mesh generation

由于计算网格的数量会影响计算精度，故本文采用几种不同的网格加密尺寸，在相同的边界条件下进行仿真计算，并将计算结果与风洞试验测试结果进行对比，几种网格验证方案和结果见表1。由表1可知，风洞试验气动阻力系数Cd为0.284，升力系数Cl为-0.047；方案3和方案4网格计算结果相同，与风洞试验的误差最小，分别为0.4%和2.1%。考虑到计算时间和计算资源，本文采用网格方案3。

表1 网格验证结果

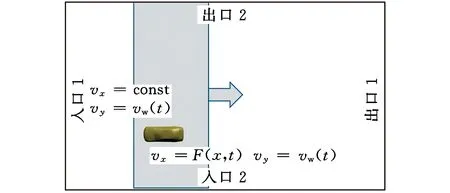
根据文献[21]可知，侧风通过入口1和入口2的合成风来模拟，得到的结果与试验更相符。由于汽车在纵向的自由度由相对速度来考虑，因此，自然侧风和ISO12021标准侧风在边界条件上有较大的不同。对于自然侧风，其入口1和入口2的合成风边界条件如图5所示。自然侧风的前部入口和侧面入口合成速度相同，其中X方向速度为汽车车速，侧向Y的速度为侧风风速。Y向速度为时间函数，根据文献[22]，函数可以写为

vw(t)=

(9)

式中,vw(t)为随时间变化的侧风速度;vw,max为侧风的最大风速，根据ISO12021取20 m/s；ts为余弦段的长度，根据文献[23]取1.5倍车长对应的时间；td为侧风稳定时间，根据文献[24]，以余弦上升和下降阶段的中间位置计算的侧风区域长度(ts+td)超过7倍车长时，侧风会发展成稳定的湍流，为了研究汽车在瞬态下的稳定性，避免发展成稳定的侧向湍流，侧风区域取为6倍车长，总侧风作用区域为7.5倍车长，满足ISO12021标准中侧风区域宽度不低于20～25 m的要求。

(a)自然侧风边界条件

(b)标准侧风边界条件图5 侧风模拟边界条件Fig.5 The boundary condition for crosswind simulation

由于汽车在纵向不产生运动，因此环境侧风的模拟采用相对运动进行处理[22]，环境侧风区域从入口1以车速相对于汽车运动。入口1处合成风速与自然侧风一致，入口2处侧向风速为时间和空间的函数，可以表示为

F(x,t)=

(10)

式中，v为汽车车速，其余参量的取值与自然侧风一致，以便于自然侧风与标准侧风的对比。

为了使汽车在流场中稳定后开始耦合，侧风在耦合开始后0.5 s开始，因此根据上述函数绘制出平移2.5 s的侧风风形，如图6所示。其中图6a为自然侧风，作用于自然侧风工况的入口1和入口2；图6b为标准环境侧风，侧风沿X轴正向移动，作用于标准侧风工况的入口2，标准侧风工况的入口1采用与自然侧风相同的瞬态侧风边界条件。

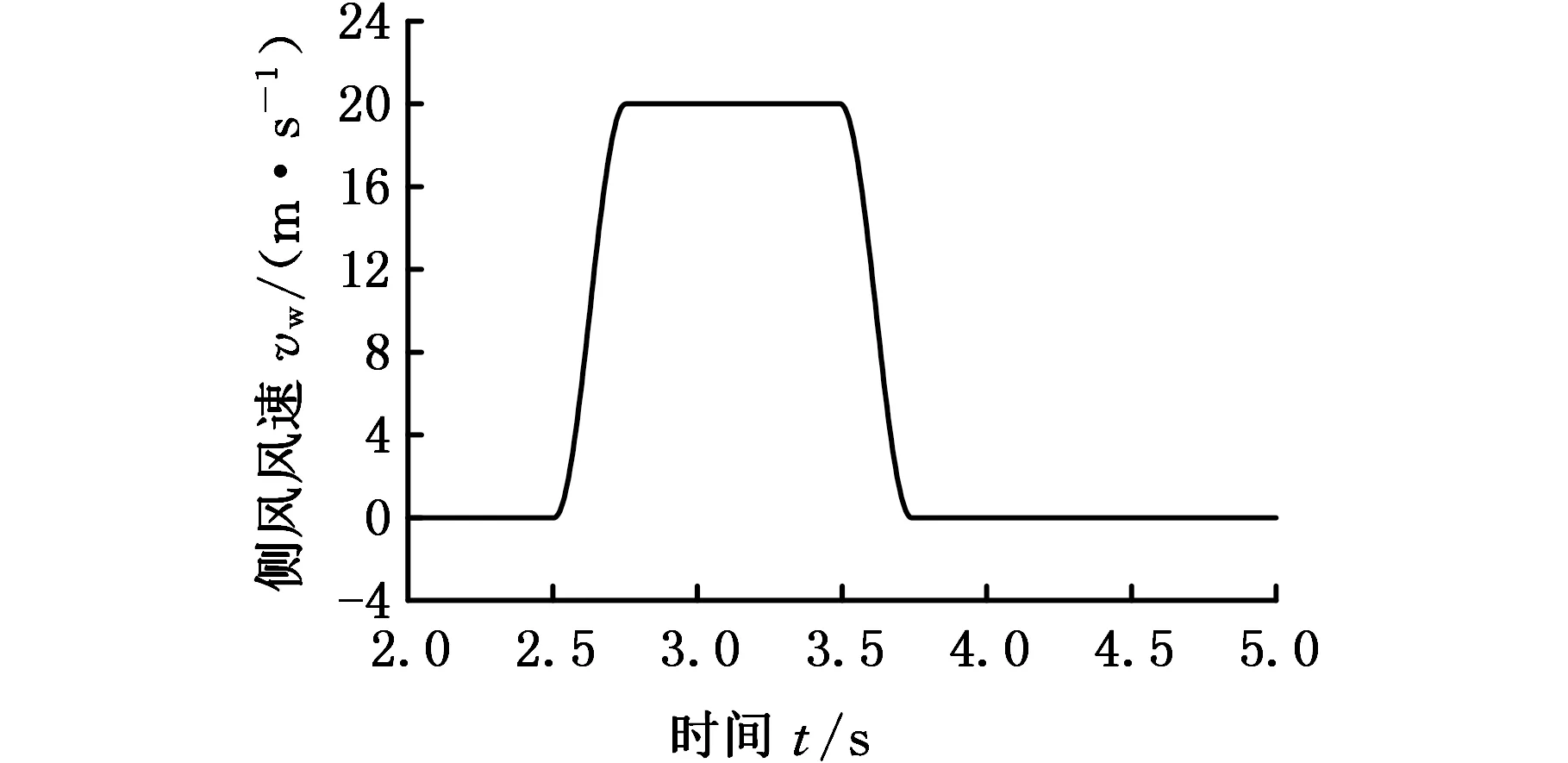
(a)自然侧风

(b)ISO标准侧风图6 自然侧风和ISO标准侧风模型Fig.6 Natural crosswind and ISO standard crosswind model

1.3 多体系统动力学计算模型

根据如表2所示的汽车整车参数，基于ADAMS/Car建立汽车多体系统动力学模型，包括完整的汽车前后悬架系统、转向系统、制动系统、车身、轮胎以及路面，如图7所示。

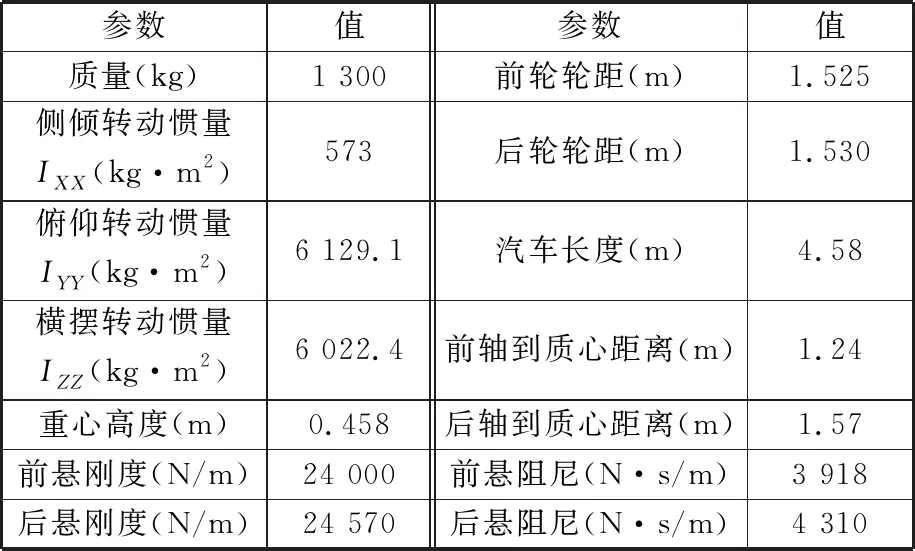
表2 汽车整车参数

根据ISO12021标准，为了减小驾驶员对汽车侧风稳定性评价的影响，在本文的侧风模拟中，汽车转向盘始终处于锁死的状态，不考虑驾驶员模型的影响。汽车轮胎采用基于魔术公式Pacejka89的185/65R15轮胎，路面采用光滑路面，路面摩擦因数为1.0。气动六分力作用于汽车刚性车身的质心，并通过运动调试，将汽车的质心高度与CFD模型调整一致。气动六分力的数值来源于实时的CFD计算，它在每个时间步进行更新，并将质心的运动反馈给CFD模型。

图7 汽车多体系统动力学模型Fig.7 Vehicle multi body dynamic model

1.4 空气动力学与多体动力学双向耦合

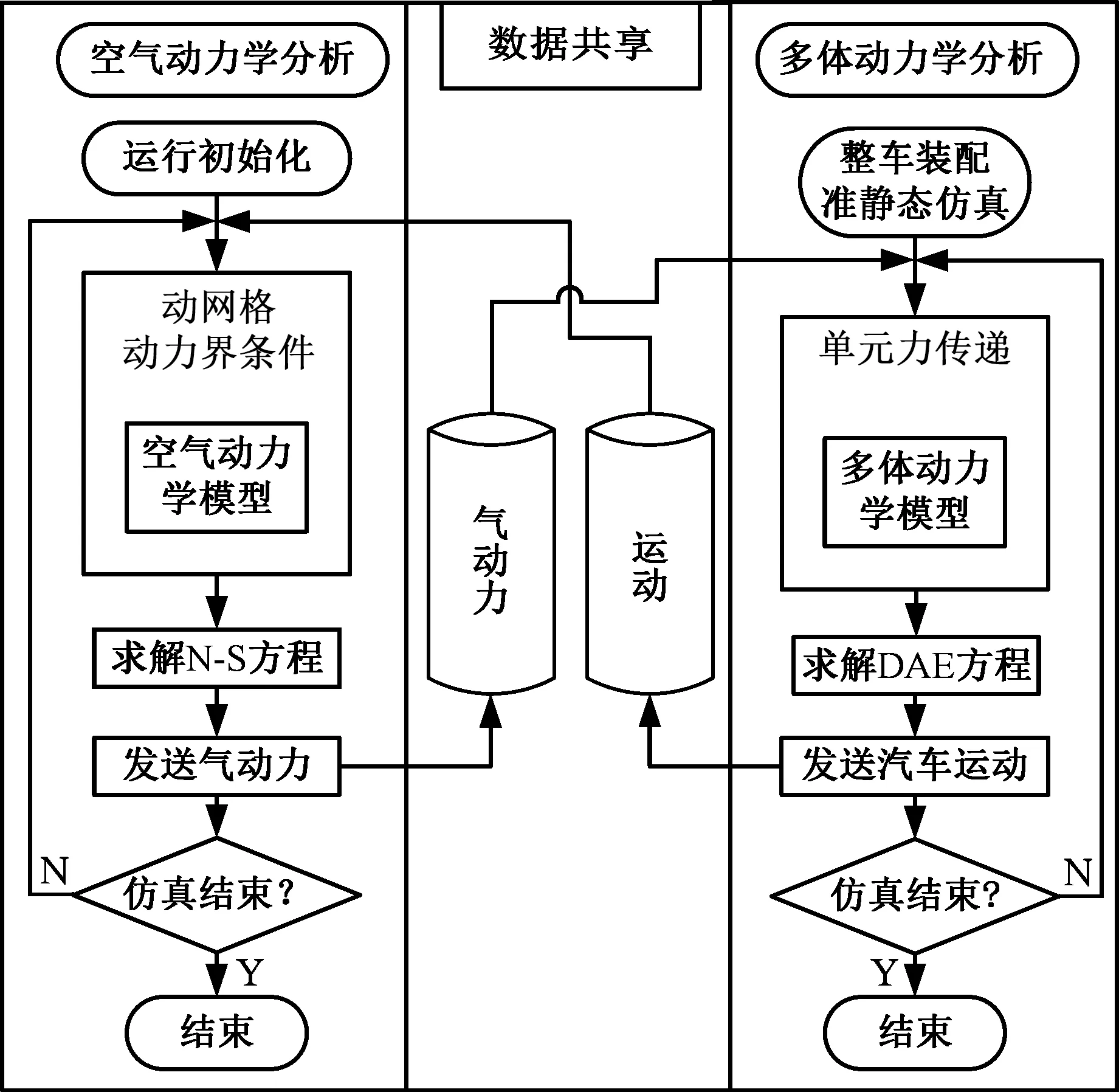
图8 双向耦合分析示意图Fig.8 The diagram for two-way coupling analysis process

双向耦合分析见图8，耦合分析同步运行在两个独立的计算模型中。在耦合开始前，空气动力学模型首先进行初始化，并进行2 s的瞬态分析，以使流场波动趋于稳定，同时多体动力学模型也进行准静态仿真，在无气动力作用下运动2 s。初始仿真之后，空气动力学模型与多体系统动力学模型进行初始数据交换。空气动力学模型中的车身接收到运动数据，求解运动网格方程，重新计算生成新网格，并进行一个步长的CFD仿真，在每一步仿真结束后，空气动力学模型发送数据到耦合服务器。同样地，多体系统动力学模型在接收到气动力后，在气动力的作用下进行动力学求解，并在每一步的仿真结束时发送质心位置运动参数，最终两个模型得以实时同步耦合，在耦合持续0.5 s之后，空气动力学模型中的自然侧风或动边界侧风开始起作用，汽车在侧风下的气动力被传递给多体动力学模型，多体动力学模型中的车身在气动力的作用下发生侧滑、侧倾、横摆、俯仰等运动，同时空气动力学模型中的车身通过ALE方法发生运动，汽车在不同姿态下的瞬态流场变化得到求解，最后仿真在耦合持续3 s之后结束。从该耦合过程可以看出，该耦合方法既考虑了汽车各个总成结构对运动求解的影响，同时也考虑了姿态变化对流场求解的影响。

2 结果验证和分析

2.1 空气动力学模型风洞试验验证

由于侧风道路试验的危险性和困难性，本文瞬态模拟方法的验证采用风洞试验的方法。在湖南大学HD-2风洞进行风洞测力和粒子图像测速(PIV)试验，该风洞高速试验段长17 m、宽3 m、高2.5 m，最大允许试验风速58 m/s，速度不均匀性大于±0.1%，紊流度大于±0.2%，高速试验段的轴向静压梯度在风速30 m/s时为0.000 16/m、风速45 m/s时为0.000 11/m,方向的不均匀性Δαi≤0.5°、Δβi≤0.5°。气动力的测量采用六分量浮框式应变天平，试验模型采用与仿真1∶3的缩比模型，主流风速为100 km/h，与仿真车速相同。在缩比模型风洞试验中，只要满足了雷诺数的近似，试验结果的精确度就是足够的[1]。而若要使风洞中的缩比模型与仿真1∶1模型雷诺数相等，计算得到的试验风速就需达到300 km/h，由于风速的提高受压缩比和动力限制，因此实现完全的雷诺数相似是不可能的，但研究表明雷诺数存在一个自准区，当模型试验的雷诺数超过某个数值时，雷诺数对流动特性的影响较小，雷诺数近似就可以实现[25]，其中美国汽车工程学会推荐该值为0.7×106，日本专家推荐该值为0.5×106，本文1∶3缩比模型的雷诺数为2.9×106，该雷诺数达到了自准区，认为该缩比模型风洞试验结果可靠，可以用于空气动力学仿真模型的验证。风洞试验现场见图9。

(a)测力试验 (b)PIV试验图9 风洞试验现场Fig.9 Wind tunnel test

风洞试验测力结果表明，该车气动阻力系数为0.284，气动升力系数为-0.047，通过网格无关性验证，方案3和方案4的网格与试验最接近，气动阻力系数误差为0.4%，气动升力系数误差为2.1%，方案4相较于方案3，网格数量虽然增加了，但气动力系数保持不变，这可能是因为在风洞中进行试验时，环境温度的测量误差和试验仪器的累计误差等原因，导致试验结果与仿真结果的误差一直存在，但该结果误差较小，在允许范围内。在横摆角0°、风速30 m/s的工况下，进行汽车尾部PIV试验，试验结果见图10，可以看到在尾部均形成了两个涡，上部为顺时针涡，下部受底部气流影响，行成一个逆时针涡。与试验相比，LES结果中上部涡结构更大，下部的涡大小相近，这是由于PIV试验中，汽车尾部区域的选择偏差可能导致汽车尾部流场结构的捕捉不足。PIV中下部位置的涡靠近地面位置的流线曲率较大，而仿真工况下相对较小，这是因为PIV中粒子在车身表面和壁面沉降较为严重，导致壁面附近的流速比仿真工况下更低，而远离位置比较准确，因此形成较大的弯折，但总体上认为，仿真结果与试验结果相近，证明了本文选择的LES数值模拟方法的可行性。

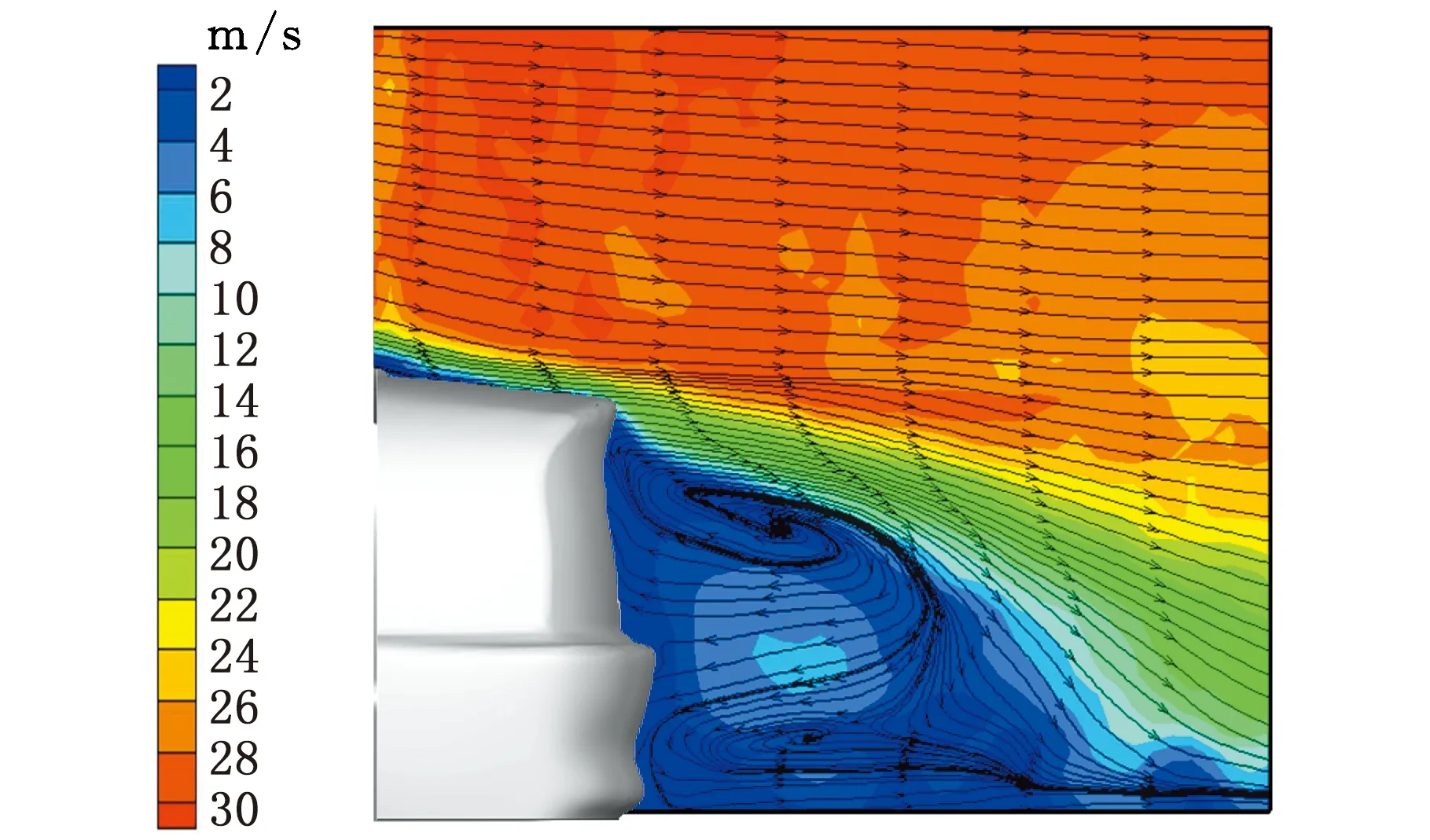
(a)PIV试验结果

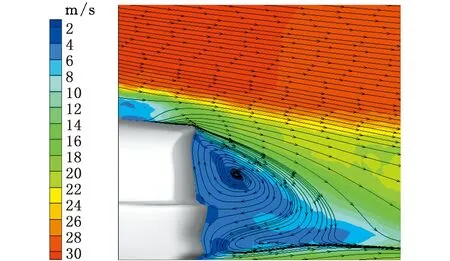
(b)LES模拟结果图10 汽车尾部流场对比Fig.10 The comparison of vehicle tail flow fluid

2.2 汽车多体动力学模型鲁棒性验证

对于汽车多体系统动力学模型鲁棒性的验证，通过改变风压中心的位置验证汽车动力学模型捕捉已知运动的能力。在汽车多体系统动力学模型中的质心位置施加一恒定侧向力，根据风压中心的定义[22]，该侧向气动力的作用点可以看作为风压中心。标准风压中心位置(CPstd)位于距离汽车前轴44%的位置。使风压中心从标准位置分别向前(CPfwd)和向后(CPbwd)，以及向上(CPuwd)和向下(CPdwd)移动两步，每步移动150 mm，分析汽车捕捉侧偏运动和侧倾运动的能力，仿真结果如图11所示。

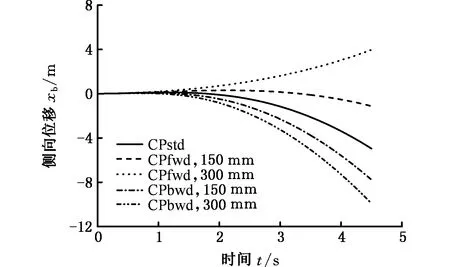
(a)风压中心前后移动

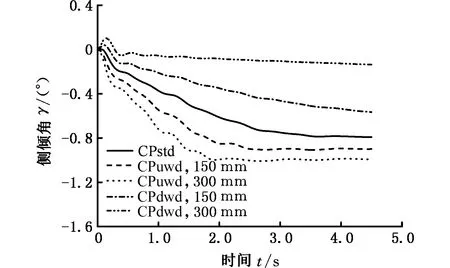
(b)风压中心上下移动图11 风压中心移动对汽车运动影响Fig.11 The impact analysis of the moving of CP on vehicle motion

由图11a可以看出，当风压中心在标准位置时，汽车向侧向反向偏移，这是因为侧向力导致汽车产生一个正的横摆力矩，汽车在横摆力矩的作用下向左侧运动，从而导致反向的侧偏位移；当风压中心向后移动时，距离越远，正的横摆力矩越大，汽车的侧向位移越大；当风压中心前移时，汽车侧向偏移减小，但向更远的位置移动时，汽车向正向偏移。这表明汽车能捕捉OXY平面的运动趋势。

由图11b可以看出，当风压中心向上移动时，产生一个负的侧倾力矩，且风压中心越高，汽车受到的侧倾力矩越大，汽车在侧向力和侧倾力矩共同的作用下产生的侧倾角也越大；当风压中心位于质心下侧时，产生一个正的侧倾力矩，且风压中心位置越低，汽车受到的侧倾力矩越大，其抵抗侧向力的作用越大，汽车在侧倾力矩和侧向力的共同作用下侧倾角也越小，这也是汽车的风压中心要尽量低的原因。这表明汽车能捕捉OYZ平面的运动变化。

汽车在侧向力的作用下，车身运动能较好地被捕捉，因此该汽车多体系统动力学模型的鲁棒性较好，适合本文的侧风稳定性研究。

2.3 汽车单双向耦合差异分析

根据ISO分析工况，采用动态边界方法模拟标准侧风，对该汽车进行了单向耦合(1 way)和双向耦合(2 way)数值模拟，计算结果如图12所示。其中，Cd、Cs、Cl和Crm、Cpm、Cym分别表示阻力系数、侧向力系数、升力系数和侧倾力矩系数、俯仰力矩系数、横摆力矩系数；Dy、Dz和Ra、Pa、Ya分别表示侧向位移、垂向位移和侧倾角、俯仰角、横摆角。

从图12a可以看出，汽车侧向力系数和阻力系数的单双向耦合的结果差异不大，因此汽车侧向位移差异也不大。在3.5～4.0 s之间，单向耦合的横摆力矩比双向耦合的横摆力矩大，因此单向耦合的汽车横摆角也大于双向耦合结果。在3.25～4.0 s之间，单向耦合的汽车侧倾力矩略大于双向耦合的结果，因此汽车的侧倾角的波动幅值也较大。气动升力在仿真过程中出现了较大的差异，因此气动俯仰力矩也产生了较大的差异，但由于汽车受重力作用，气动升力对汽车垂向位移的贡献较小，波动相对较小，俯仰角也就较小。这也说明，气动升力和横摆力矩对汽车车身姿态的变化更加敏感。

图13为3.5 s和4.0 s时刻汽车车身表面压力云图，可以看出，在迎风侧汽车表面压力差异不大，然而在背风侧压力差别较大，在总体趋势上，双向耦合的背风侧压力略高，特别是在尾部和C柱区域，这也是侧倾力矩和横摆力矩差异比较明显的原因。

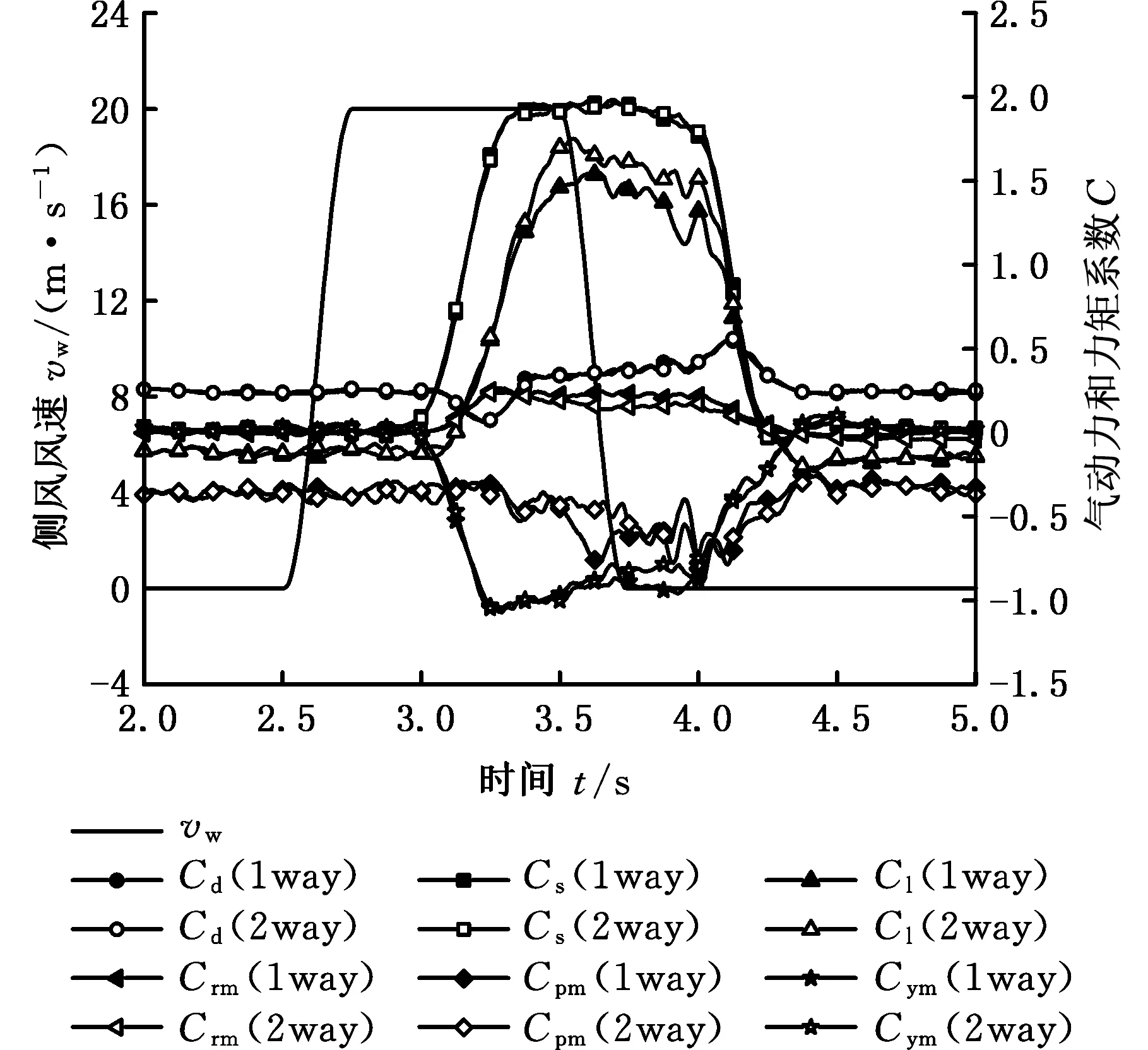
(a)单双向耦合气动力系数对比

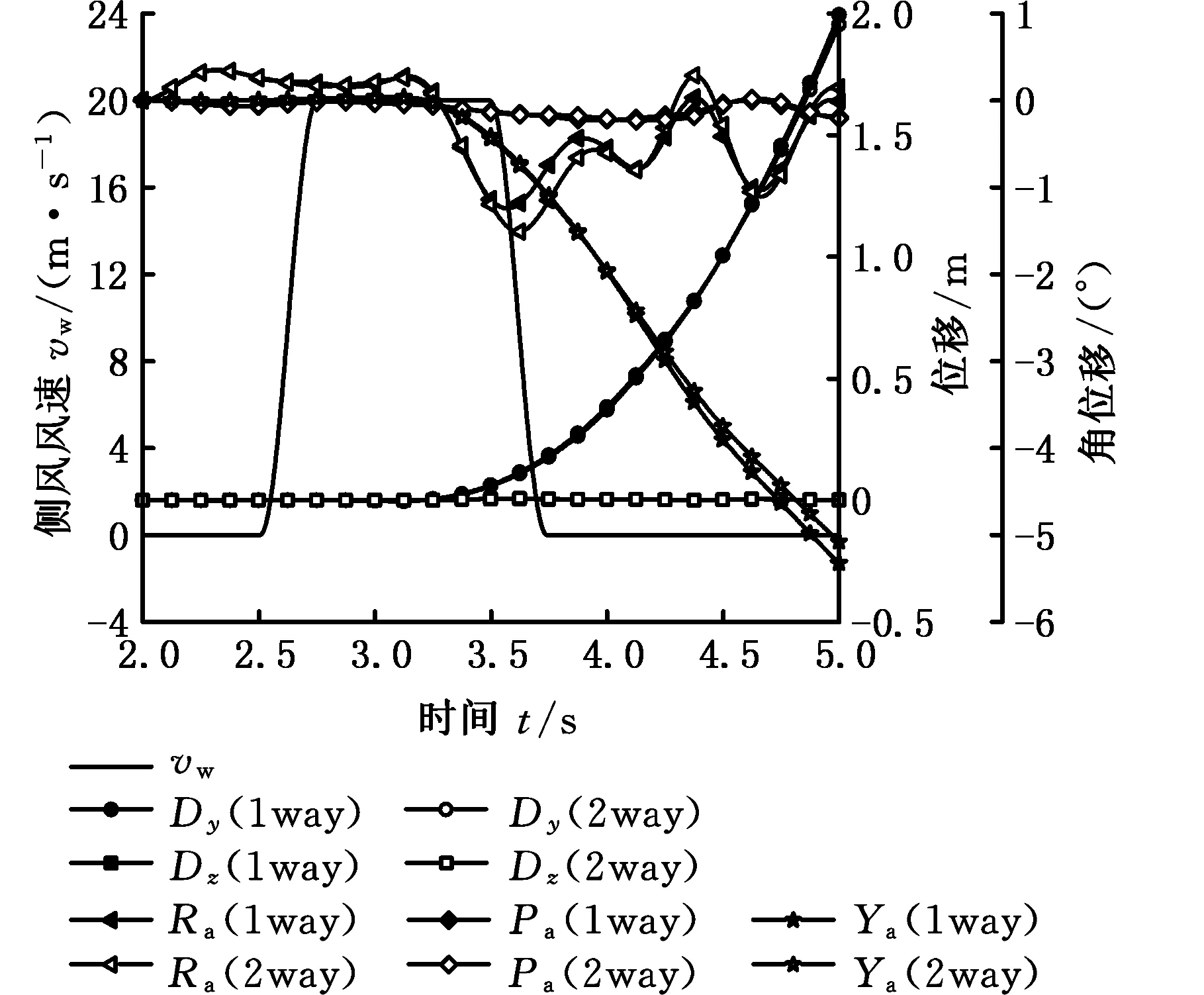
(b)单双向耦合汽车位移变化对比图12 ISO工况下单双向耦合结果对比Fig.12 The comparison of results of one-way coupling and two-way coupling under ISO condition

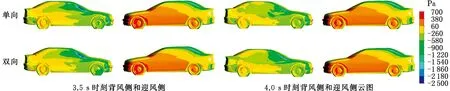
图13 3.5 s和4.0 s时刻汽车侧面压力云图Fig.13 The pressure contour on vehicle both sides at t=3.5 s and t=4.0 s

3.5 s时刻的汽车顶部和底部压力云图见图14，在汽车顶部和迎风侧的A柱均出现了较大的正压区域，而在背风侧的A柱出现气流的分离，单双向耦合的差异并不明显。在汽车的底部，很明显地可以观察到前部迎风侧车轮产生的气流分离导致的负压区域，相较于单向耦合结果，双向耦合的负压区域较小，这是由于双向耦合中汽车发生了侧倾运动，汽车底部流入了更大的气流，底部压力升高。此外，背风侧的前后车轮处均产生了较大的压力集中，且双向耦合中，由于更大的底部气流，这种现象也更加明显，因此在车轮处产生了更大的压力，图12中的侧倾运动与升力变化的单双向耦合差异也较大，由此可知有必要采用双向耦合分析方法研究汽车运动对气动力的影响。

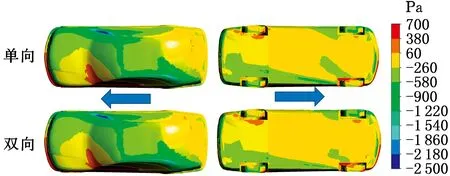
图14 3.5 s时刻汽车顶部与底部压力云图Fig.14 The pressure contour on vehicle top and bottom at t=3.5 s

2.4 侧风形式对汽车侧风稳定性影响研究

以瞬态边界和动态边界方法分别对汽车的侧风稳定性进行双向耦合仿真，汽车在遭遇侧风影响时的速度云图见图15，可以看到在自然侧风的工况中，在3.0 s时，汽车已经完全进入侧风区域，并且风速达到最大，这是由于侧风从2.5 s开始施加于前侧和左侧入口，3.0 s时刻侧风边界条件已经达到了最大值，并且已经运动到车身位置，在3.5 s时侧风风速开始降低，但侧风的作用并没有消失，汽车仍旧受侧风的影响，4.0 s时，侧风风速逐渐降低，在4.5 s时，汽车完全退出侧风作用区域，5.0 s时，侧风完全消失。标准侧风则完全不同，可以看到，虽然侧风边界条件从2.5 s时就开始起作用，但直到3.0 s前后时，汽车头部才最先接触到侧风，并且风速逐渐增加到最大，在3.5 s时，汽车已经完全进入侧风区域，从4.0 s时，汽车开始退出侧风区，最终4.5 s时汽车完全穿过侧风区域，在5.0 s时侧风消失。这表明自然侧风对汽车的影响更加迅速，并且侧风对汽车的作用是全局的，整个车身侧面同时受到侧风影响；而标准侧风的影响是缓慢地从车头到车尾逐渐受影响。

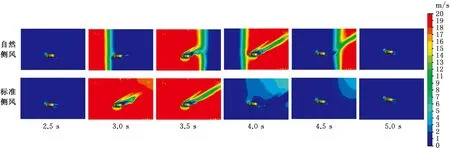
图15 汽车遭遇两种不同侧风时的侧向速度云图Fig.15 Velocity contour in Y direction when vehicle come across two different crosswind

上述两种工况下，汽车的气动力系数时间曲线如图16所示，可以看出，在自然侧风作用下的汽车气动力系数均比标准侧风下的要早0.5 s，这正是由于自然侧风作用于全局，使得侧风几乎没有任何延迟地作用到车身。此外，自然侧风的阻力系数Cd在侧风风速达到最大加速度值的时刻出现了一个较大的峰值，此后又减小并稳定，而标准侧风的阻力系数并没有出现峰值，而是逐渐地增大并稳定。这是因为自然侧风迅速地在全区域增加的时候，流场还未稳定，左侧压力较高，而右侧较低，从而导致较大的压差侧向力，与此相同，当自然侧风风速降低并消失时同样出现了一个峰值，这是因为汽车背风面的侧风依旧存在，而迎风面的侧风已经开始下降并消失，不稳定的流场因此导致一个较大的负压。对于标准侧风工况，由于侧风区域逐渐靠近车身，汽车车身受到的侧向力逐渐增加，左右两侧的侧风基本上同时向后方移动，因此并没有出现自然侧风工况下的峰值。

图16 不同侧风下汽车气动力系数变化曲线Fig.16 The variation of aerodynamic force coefficients in two different crosswind

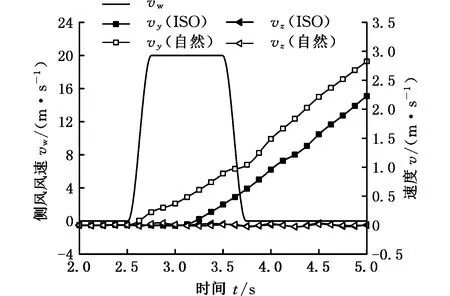
(a)汽车运动速度

(b)汽车运动角速度图17 不同侧风下汽车运动速度变化曲线Fig.17 The variation of vehicle velocity in two different crosswind

图17描述了汽车在多体系统动力学模型中的汽车运动速度。图中，vy与vz分别表示汽车的侧向速度和垂向速度；Rr、Pr与Yr分别表示汽车的侧倾角速度、俯仰角速度及横摆角速度。由图17a可以发现，在自然侧风下，自侧风开始的瞬间起，汽车的速度便急速增大，而标准侧风的工况中，汽车在侧风开始后的0.5 s开始运动。可以看到自然侧风作用下的汽车侧向速度曲线出现两次转折，标准侧风工况下的汽车侧向速度曲线相对平滑。在侧风消失后，汽车依旧具有侧向的偏移速度，这是因为汽车的方向发生了横摆之后，汽车的纵向运动速度沿Y轴的分量依然存在，因此汽车的侧向偏移速度没有因为侧风的消失而降低。汽车的垂向运动速度较小，且一直处于波动状态，但可以看出自然侧风工况下汽车的垂向运动速度更大，波动更剧烈。由图17b可以发现，在自然侧风作用下，侧风开始时，汽车的侧倾角迅速产生较大的波动，而在侧风消失时也产生了较大的反向侧倾角速度波动。侧风接触汽车时，在自然侧风下的汽车侧倾角速度大于标准侧风下的侧倾角速度，而标准下的侧倾角速度变化周期大于汽车在自然侧风下的变化周期，这也表明汽车在自然侧风作用下的运动变化更剧烈。而在侧风离开汽车时，标准侧风作用下的汽车侧倾角速度大于自然侧风作用下的侧倾角速度，这主要是因为汽车的侧倾受到悬架结构的影响，自然侧风下的汽车侧倾角小，悬架对车身的作用也较小，而标准侧风下的汽车侧倾角较大，车身受悬架影响也较大，具体的侧倾角位移变化如图18所示。对于汽车的俯仰运动，在自然侧风环境中，汽车的俯仰角速度变化也较标准侧风更加剧烈，但两种工况下的角速度峰值基本相同。对于汽车的横摆运动，可以看出，无论在哪种环境中，在侧风作用期间，汽车的横摆角速度都逐渐增大，当侧风降低至消失后，汽车的横摆角度都有略微的降低，但并没有趋向于零，从而导致汽车的横摆角逐渐增大。

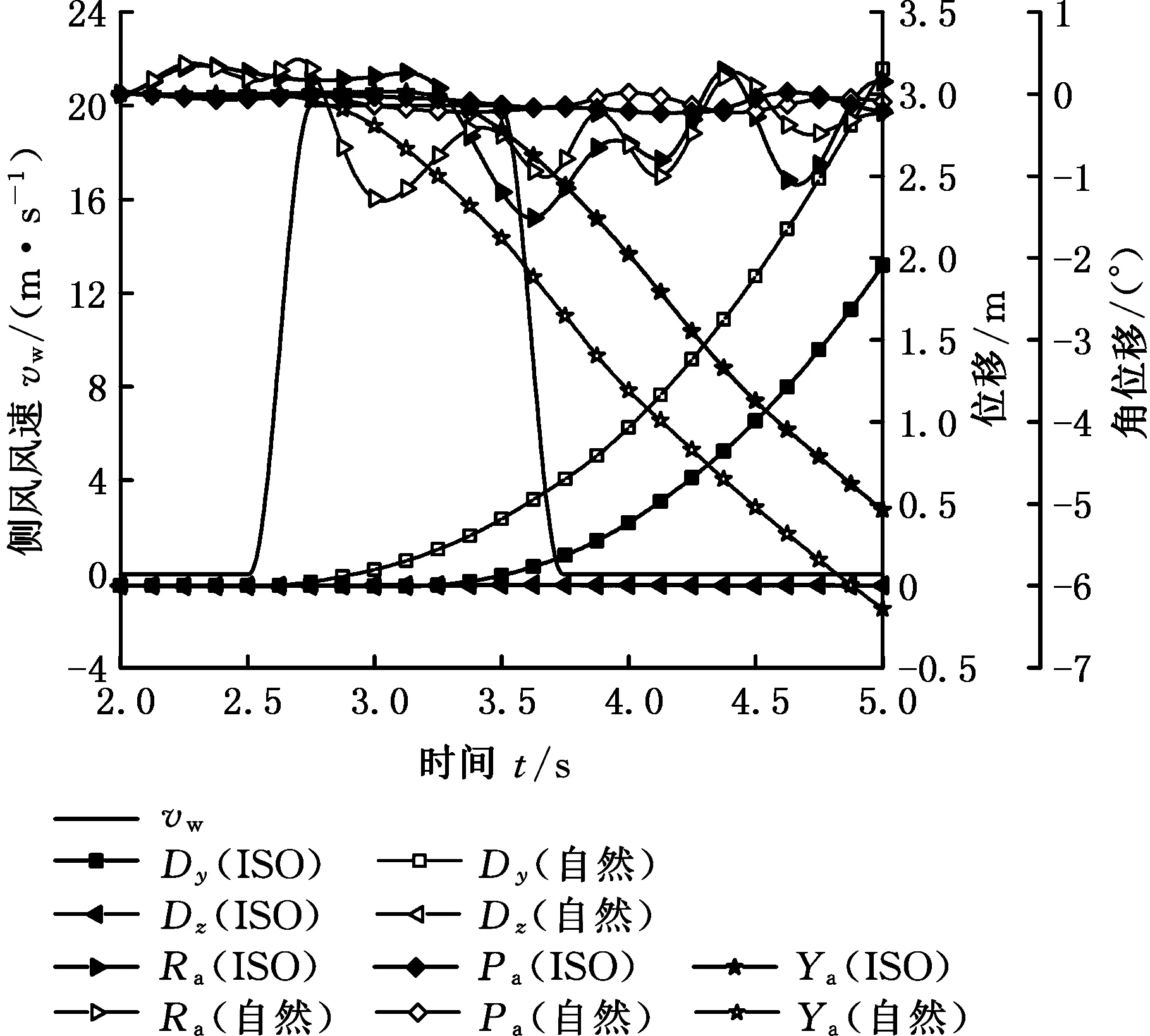
图18 不同侧风下汽车位移变化曲线Fig.18 The variation of vehicle displacement in two different crosswind

标准侧风和自然侧风两种工况下汽车的运动位移如图18所示。按照ISO标准，汽车在侧风的作用下，从2.5 s开始至4.5 s时，标准侧风和自然侧风下的汽车侧向位移分别为1.01 m和1.89 m，而在本文的仿真结束的5.0 s时，汽车的侧向位移达到1.96 m和3.15 m。这两种工况下的汽车侧偏位移均在标准中的5 m的范围内，但是根据文献[26]，在中国的高速公路上，汽车侧偏达到0.975 m就已经非常危险了，所以汽车在2 s内的位移偏移依旧过大，直接影响了汽车的行驶安全性，而且自然侧风对汽车的影响更大，标准中对汽车侧偏位移的评价略显不足。除此之外，汽车的横摆角变化也非常大，标准侧风作用下汽车的横摆角在2 s内达到了1.96°，而自然侧风下的横摆角更大，为3.62°。图17中汽车的横摆角速度虽然都在减小，但是并没有降低为零，因此汽车在后续的0.5 s内继续侧偏，在0.5 s内横摆角分别增加了3.11°和2.66°。这是因为标准侧风相对于自然侧风存在0.5s的时间滞后，但即便考虑到标准侧风的滞后，它对汽车横摆角变化的影响依旧小于自然侧风。对于汽车的侧倾角变化曲线，可以看到，在侧风作用开始时，虽然自然侧风作用下的汽车侧倾角速度较大，但其侧倾角小于标准侧风作用下的侧倾角，这主要是因为此时汽车在标准侧风作用下的角速度变化周期较长，而自然侧风作用下的汽车角速度变化周期较短。在侧风作用期间汽车的侧倾角一直在小于零的位置波动，这是由于汽车的侧倾角变化受侧倾力矩和悬架作用的共同影响。在侧风消失时，汽车在稳态自然侧风下的侧倾角波动依旧小于零，而标准侧风作用下的汽车侧倾角出现了反向的波动，这主要是因为此时汽车受到的气动力与悬架作用方向一致的原因，这也进一步说明了采用双向耦合分析方法的必要性。同时，这也导致了图17b中，在4.5 s时汽车的侧倾角速度出现了较大的反向波动。

综上结果表明，自然侧风下汽车的气动力作用更加迅速，对汽车周围流场的影响也更大，特别是在侧风加速和减速期间，流场更加不稳定，汽车的运动也因此相较于标准侧风更加剧烈，而标准试验中的标准侧风对汽车稳定性的评价稍显不足，对于国内汽车的侧风稳定性的评价，需要根据国内道路情况进行考虑。