基于网格曲面形状修改的柔性件装配偏差分析
2019-10-25苏成阳王志国
苏成阳 王志国
南京航空航天大学机电学院,南京,210007
0 引言
在柔性件装配生产过程中,因形状误差、夹具定位误差、材料误差等因素的耦合作用,使得装配偏差不可避免,严重影响了产品的装配质量。为了提高零部件装配的成功率和产品质量,国内外研究人员针对柔性件装配偏差分析开展了大量的研究工作。
在国外,LIU等[1-3]率先对柔性件装配偏差分析进行研究,将柔性件的装配过程划分为定位、夹紧、铆接、释放夹具4个步骤,并建立用于分析柔性件装配的有限元模型,在此基础上使用影响系数法(method of influence coefficients, MIC)建立了装配偏差与柔性件制造误差的线性关系。为了进一步减小确定性定位造成的回弹变形,CAI等[4]提出了N-2-1定位法并应用于柔性件的固定。以上研究尚未考虑零件接触,DAHLSTRÖM等[5]在影响系数法的基础上提出了应用于柔性件装配的接触算法,并在此基础上建立了有限元柔性件接触分析模型,提高了柔性件偏差分析的可靠性。为了将装配偏差理论扩展至多工位装配领域,CAMELIO等[6]建立了多工位偏差传递模型,研究了单个工位中制造误差、夹具偏差、焊枪位置误差对后续装配的影响。GERBINO 等[7]研究了形状误差、定位偏差、重定位误差在多工位装配过程中的传递,并使用蒙特卡洛法结合有限元法验证了误差传递流模型的正确性。在柔性件表面形状误差表达方面,BIHLMAIER[8]使用频谱分析检测表面数据,运用自相关谱描述了误差变化的几何连续性。TONKS等[9-10]使用正弦多项式和勒让德多项式混合的方法表达柔性件表面的波动偏差和翘曲偏差,建立了几何协方差模型。
在国内,田兆青等[11]研究了多工位薄板装配过程中偏差流传递、变换和累积关系的状态空间模型。文泽军等[12]引入销/孔公差,提出了一种面向产品质量的薄板装配工艺系统可靠性建模方法。胡朝辉等[13]针对汽车车身设计未考虑装配误差的现象,建立了焊接装配偏差模型,从而实现对车身装配偏差的控制。在飞机装配领域,谭昌柏等[14]运用稳健设计方法建立了飞机装配公差的可行稳健性和敏感稳健性两类设计模型。陈晖等[15]运用勒让德多项式和正弦多项式的混合形式表达柔性表面形状偏差,建立了耦合材料误差和形状误差的有限元分析模型。张玮等[16]提出了一种使用夹具主动补偿的装配偏差优化方法,进一步减小了柔性件的装配偏差。崔志卓等[17]提出了一种有向点集装配协调数学模型,有效提高了航空领域多孔多面装配成功率。
实际生产中,零件的外形存在随机误差,同一批次的零件外形存在差异。以测量为手段获取每个零件实际外形,并使用有限元法进行装配偏差分析的效率极低。考虑到零件制造误差较小,以往的研究是在零件理论外形基础上提取敏感度矩阵进行装配偏差分析,然而此方法分析结果的准确性有待研究。本文提出一种装配偏差分析改进方法,根据误差源数据和理论外形,使用网格曲面修改方法得到所谓的“实际外形”,以此模型对应的敏感度矩阵进行装配偏差分析,以期在传统方法的基础上大幅提高装配偏差分析准确性。
1 柔性件装配偏差建模
柔性件的装配大致可分为定位、夹紧、铆接、回弹释放等4个过程,每个过程均需进行力学建模。
1.1 定位
柔性件装配中大部分采用N-2-1定位(图1),具体操作如下:首先使用确定性定位(3-2-1定位)将柔性件固定在夹具上;然后对该柔性件施加外力,将过定位点夹持至名义位置,以保证零件装夹的稳定性。

图1 N-2-1柔性件定位法示意图Fig.1 N-2-1 locating method of compliant parts
该过程在有限元方法中可视为对过定位点施加强制位移约束,以图1中的A板为例,可得
(1)
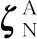
同理,B板在此过程中的力学方程为
(2)
1.2 夹紧
该阶段中通过外力将A、B板的铆接点夹持至名义位置,同样可视为对板料的铆接点施加强制位移约束,如图2所示。类似地,此过程中受力与变形的关系可以表示为
(3)
(4)
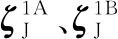
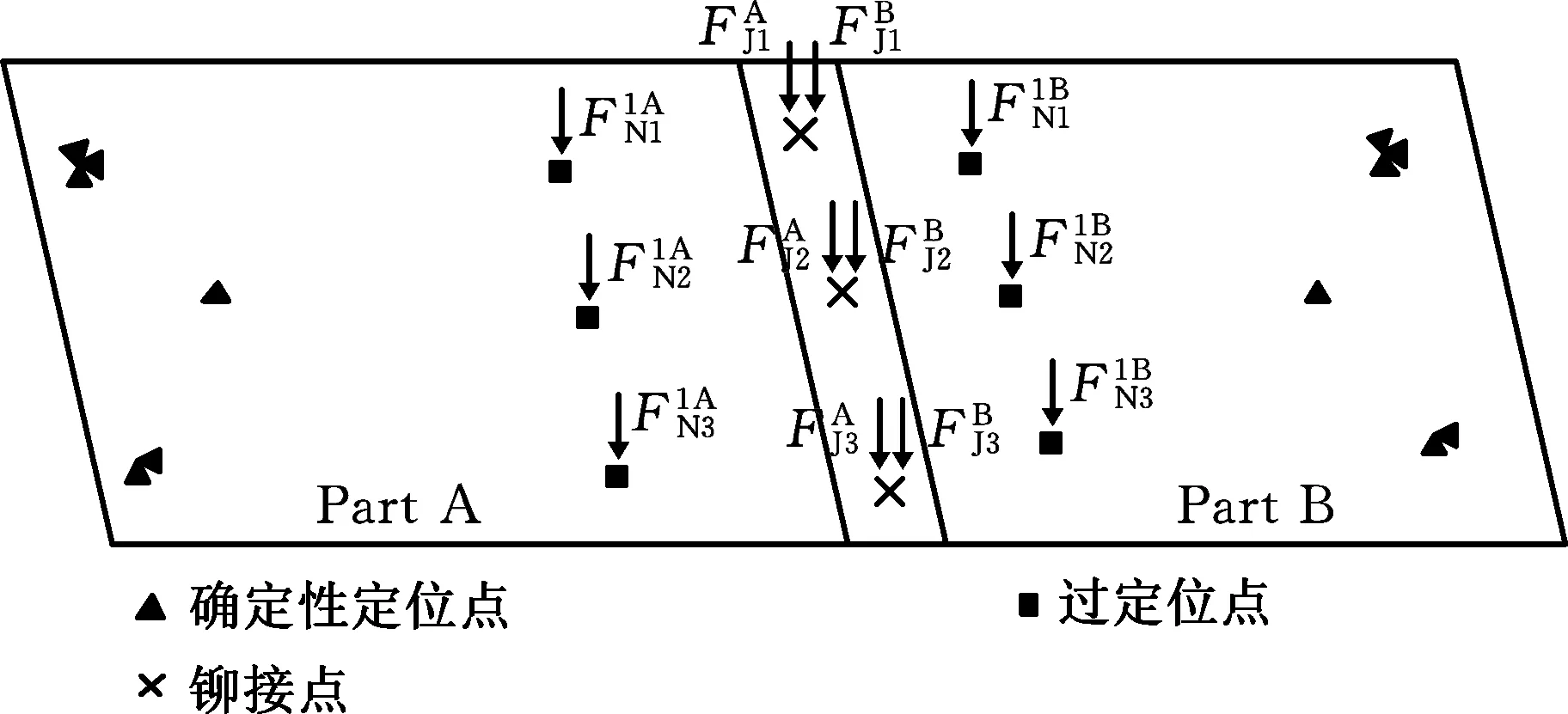
图2 柔性件夹紧示意图Fig.2 Clamping of compliant parts
(5)
装配点处的夹紧力
(6)
1.3 铆接及释放回弹
零件夹紧后,使用工具在铆接点处进行铆接以形成装配体,此过程中由温度或铆钉挤压力等因素导致的装配偏差本文不予考虑。
由于零件存在不可避免的制造误差,故装配过程中必然会存在装配应力,当铆接完成后,需要释放过定位处装配点处的夹具,装配体则会产生回弹变形,如图3所示。

图3 装配回弹示意图Fig.3 Rebounding of assembly
A板和B板在过定位点以及铆接点处的回弹力可定义为式(5)和式(6)中的夹紧力[3],大小相等且方向相反,表达式为
(7)
因此,装配体的回弹变形可以表示为
(8)
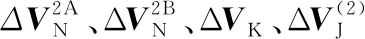
上述的超元刚度矩阵可通过商业有限元软件提取。由式(1)~式(8)可推导得到装配偏差与制造误差的关系:
[ΔVKΔVJ]T=S[ζNζJ]T
(9)
式中,S为敏感度矩阵;ΔVK、ΔVJ为KPC点、铆接点处的装配偏差;ζN、ζJ为过定位点、铆接点处的制造误差 。
本文仅对柔性件装配偏差分析计算框架进行简要的介绍。详细计算分析过程可参考文献[1-3]。
2 理论数模的偏差计算准确性分析
由于零件的制造误差为随机量,故每个实际生产的零件的外形必然存在差异。考虑到零件制造误差相对较小,在小变形、线弹性的前提下,柔性件偏差分析的敏感度矩阵可从零件理论外形的有限元模型中获取。由此,传统的偏差分析方法可认为是一种近似的手段,其近似程度如何是值得商榷的。本文对传统方法的分析准确性进行研究。
2.1 理论数模与实际数模的有限元模型
在商业软件ABAQUS中建立A、B两块平板作为理论数模,长宽皆为600 mm×400 mm,再建立两张曲面,模拟A、B板的所谓实际外形,分别进行有限元模型的设置。算例中各板采用S3R三角形壳单元划分单元格,数量为2 160。材料参数如下:厚度为3 mm,泊松比为0.3,弹性模量为210 GPa。图4所示为理论数模与实际数模的有限元模型。

图4 理论数模与实际数模Fig.4 Theoretical mathematical model and actual mathematical model
图4中,N1~N6为A、B板的过定位点位置,J1~J3为铆接点位置,K1~K3为选取的观察装配偏差的KPC点。A、B板实际模型在过定位点、铆接点沿Z向的误差如表1所示。
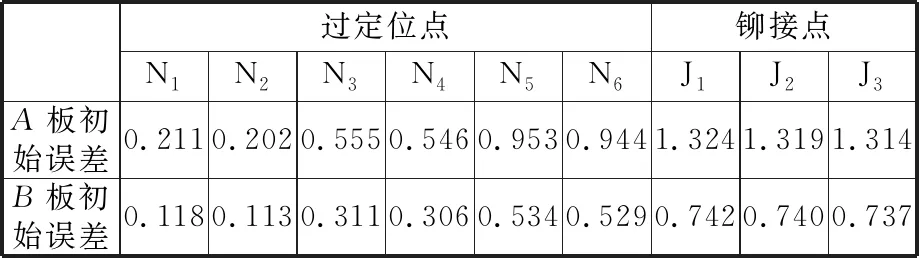
表1 A、B板的初始制造误差
2.2 理论数模与实际数模的分析结果对比
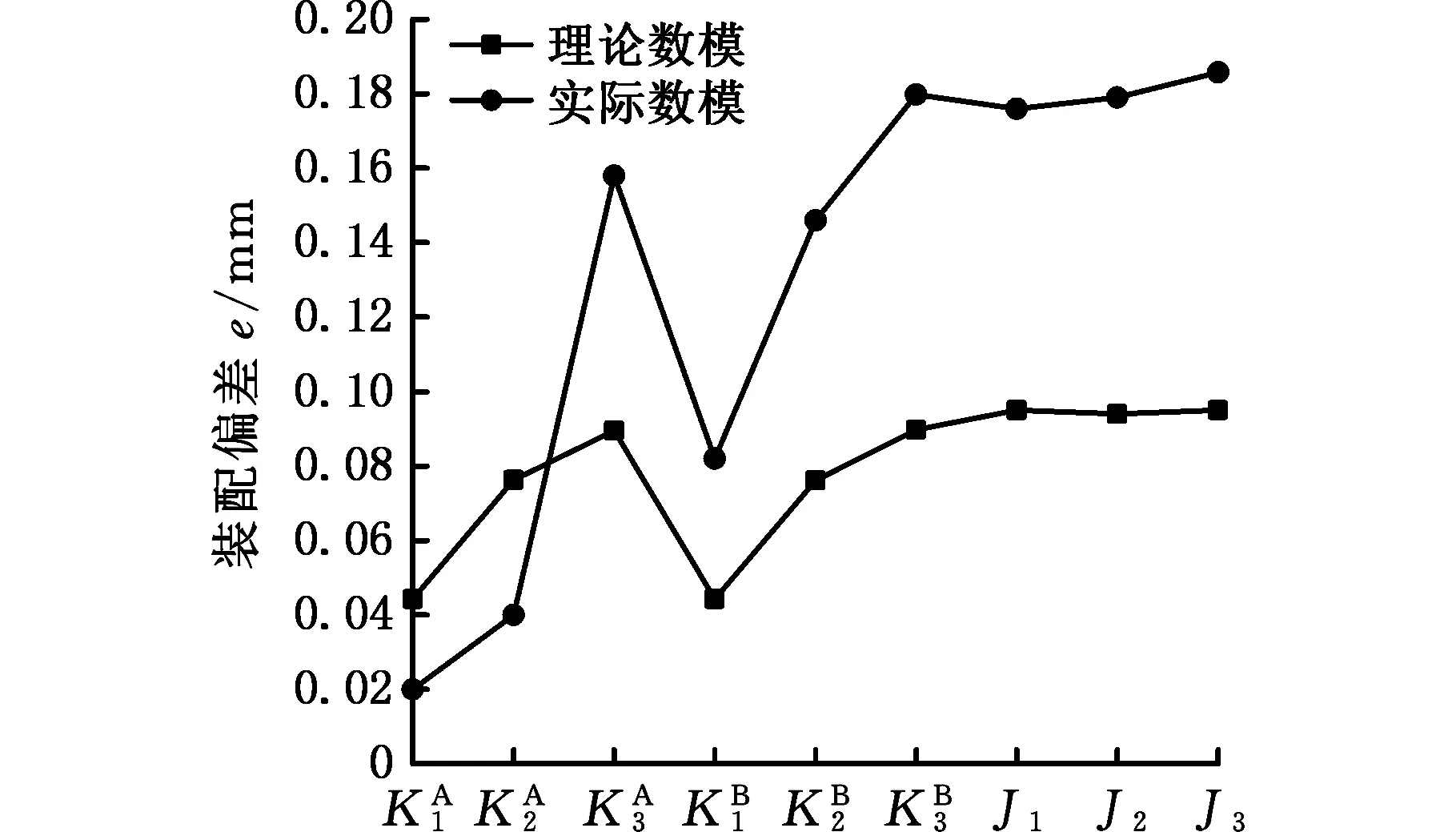
图5 回弹结果对比Fig.5 Comparison of rebound quantity

Tab.2 Analysis error rate of KPC points& joining points on assembly%
由图5及表2数据可知,基于理论数模的装配偏差分析结果相对实际数模误差非常大。考虑到理论数模与实际数模的材料信息、网格拓扑结构及误差源数据一致,误差可认为由两者的敏感度矩阵,即产品的理论外形与实际形状不一致所导致的。
理论上,每生产一个零件均能用相关技术手段(如逆向工程)获取其实际外形数据,但如此操作会造成分析效率非常低下。若能从已有的条件(误差源和理论外形)逼近出所谓的产品实际外形,将会极大地提高偏差分析的效率以及准确性。本文借鉴CAD理论中的曲线、曲面形状修改技术,给出了一种柔性件偏差分析的改进方法。
3 基于拉普拉斯矢量的曲面形状修改
曲面形状修改的本质是一种形状优化方法,零件的理论外形上对应点与误差数据之和即为实际形状所要通过的目标点。修改后的曲面形状不仅能通过给定的目标点,而且要求修改前后的曲面形状比较接近,因此,形状优化的目标函数显得尤为重要。下文称曲面修改后的模型为逼近模型,即零件实际形状的近似模型。
3.1 三角网格模型拉普拉斯矢量的表示
三角网格模型可表示为T=(V,E,F)。V代表局部坐标系下所有顶点的坐标,E代表模型所有的边信息,F代表模型所有的三角形单元信息。令模型的顶点数量为q,每个顶点Vi的坐标为vi(i=1,2,…,q),对应的拉普拉斯矢量[18]可表示为
(10)
其中,N(i)={j|(i,j)∈E,j≠i}为Vi的一阶邻域。di为Vi一阶邻域中节点的数量,其示意图见图6。
各顶点的坐标V和拉普拉斯矢量δ的关系为
LV=δ
(11)
其中,L为q×q的拉普拉斯转换矩阵,其i行j列的元素可以用下式表达:
(12)
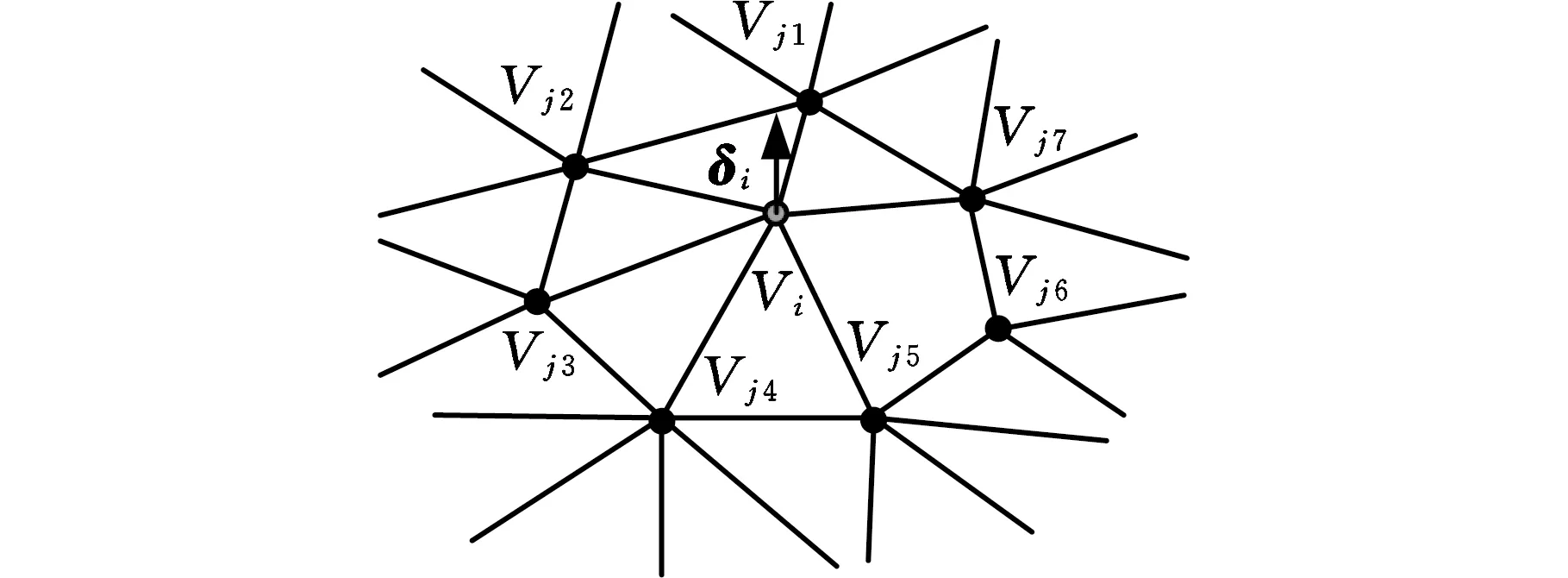
图6 拉普拉斯矢量Fig.6 Laplacian vector
3.2 基于拉普拉斯矢量的形状优化
拉普拉斯矢量近似描述了顶点处的平均法向曲率。若要求修改前后的曲面形状比较接近,可令两者对应的顶点处拉普拉斯矢量变化量最小。因此,优化目标函数为
f(V′)=‖L(V′)T-δT‖
(13)
其中,V′(v′1,v′2,…,v′n)为修改后模型所有节点的坐标,为未知量。
约束点分为重合点和目标点两类,如图7所示。其中,C(c1~c3)为重合点,用于维持原曲面的局部特征,变形前后坐标值不变;E(e1~e2)为目标点。ζe1、ζe2为E点制造误差(误差源),其误差数据可通过制造厂里的数字化测量装备或传统实物检具获取。

图7 约束点位置Fig.7 Location of point constraints
令约束点的数量为Q,每个点对应的索引号为hi(i=1,2,…,Q),由约束点建立的约束方程如下:
(14)
式中,Vh为1×Q的约束点坐标;Ih为所有节点到约束点的转化矩阵,大小为Q×q(图8)。
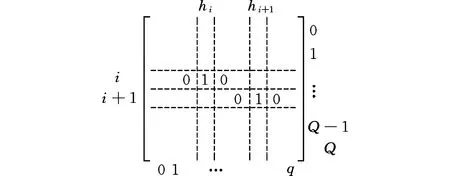
图8 约束点坐标转换矩阵Fig.8 Coordinate translate matrix of point constraints
该优化问题的数学描述可表达为
(15)
对带约束的优化问题可采用罚函数法进行求解。尽管罚函数法只能得到方程组的近似解,不过随着罚因子的增大,近似解将逐渐收敛到精确解。对式(15)构造罚函数方程:
(16)
其中,θ为罚因子。令∂E/∂V′=0,可得
(17)
求解式(17)可得到逼近模型的曲面外形。
本文结合VC+ +平台与OpenGL,实现基于理论数模的拉普拉斯网格曲面变形算法。以飞机装配中常使用的角片模型为例,图9演示了在多点约束下,角片由理论数模变形到逼近模型的过程。
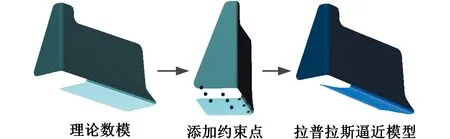
图9 角片的拉普拉斯变形Fig.9 Laplace deformation of clip
4 改进方法的偏差准确性分析
4.1 金属薄板装配试验及数据分析
试验使用铝合金板A、B进行搭接装配。材料参数如下:弹性模量为68.9 GPa,泊松比为0.330,理论尺寸均为400 mm×400 mm,厚度为1.5 mm。试验中使用Atos光学扫描仪进行外形测量,可获取装夹前、回弹后零件的外形,见图10。运用CATIA软件可得到零件的实际曲面外形,采用S3R划分单元格后的有限元模型见图11,图11中,D11~D13、D21~D23为A、B板上确定性定位夹具夹持位置,N11~N13、N21~N23分别为A、B板过定位夹具夹持位置,J1~J3为A、B板上对应的铆接点位置,K11~K13、K21~K23分别为A、B板上选取的KPC点,后文中的变量含义与此相同。A、B板上过定位点与铆接点沿Z向的初始制造误差如表3所示。图12展示了A、B板实际数模上选取的约束点位置。

图10 铝板Atos外形测量Fig.10 Atos measurement of aluminum sheet
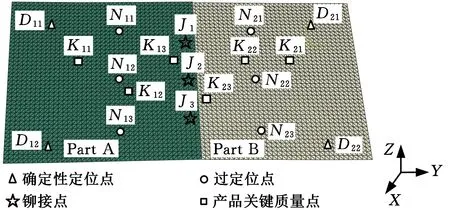
图11 铝板装配有限元模型Fig.11 FEM model of aluminum sheet assembly

Tab.3 Initial manufacture errors of aluminum sheet mm

图12 铝板的约束点示意图Fig.12 Point constraints on aluminum sheet
运用拉普拉斯变形技术,针对图12的曲面形状得到逼近模型后,可结合表3误差数据计算得到装配偏差。图13所示为试验中释放回弹后光学测量得到的点云数据,以此作为分析比较的依据。

图13 铝板装配体点云数据Fig.13 Aluminum panel assembly point cloud data
各类装配偏差分析数据沿Z向的分量对比如图14所示。由图14可知,若以试验数据为参考量,理论数模计算结果存在很大的分析误差,而实际数模和逼近模型的计算结果与试验数据比较接近。分析结果表明,改进方法在实际数模难以获取时,可有效减小分析误差。
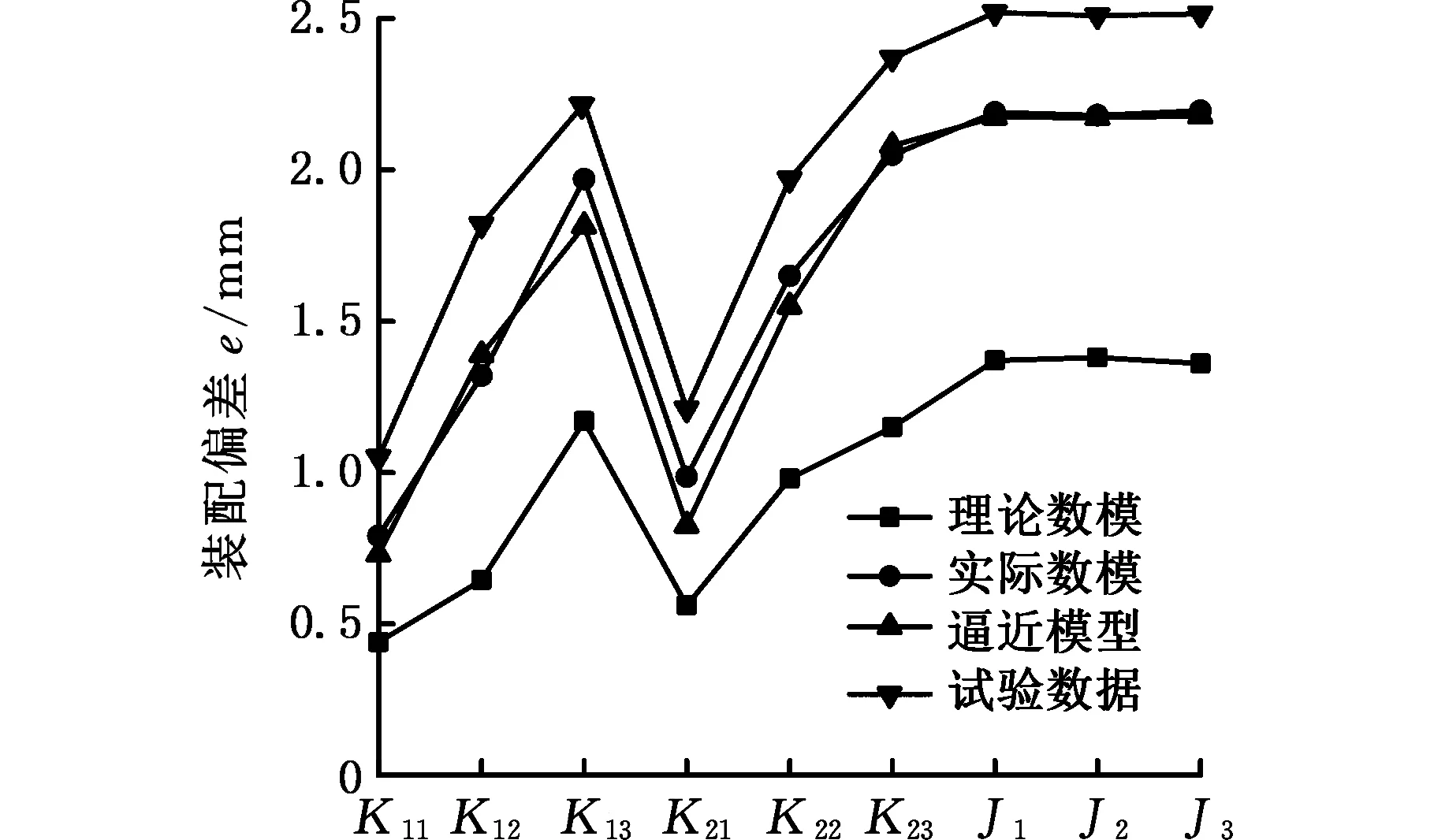
图14 铝板装配分析结果对比Fig.14 Aluminum sheet assembly result comparison
4.2 机身壁板件装配模型验证
壁板件是飞机柔性件的重要组成部分,其装配偏差分析对提高产品质量有重要意义。壁板件装配简化模型见图15。
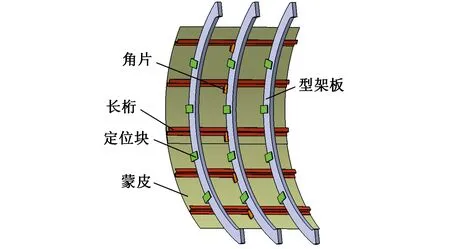
图15 壁板件装配简化模型Fig.15 Aircraft fuselage panel assembly model
在ABAQUS中建立的壁板件有限元实际分析模型见图16。蒙皮实际数模的曲率半径分别为1 975 mm、1 990 mm。理论数模的曲率半径为1 985 mm。蒙皮、角片、长桁的材料参数如下:弹性模量为73 GPa,泊松比为0.3,厚度为4 mm,本例不考虑长桁、角片的制造误差。

图16 壁板件有限元装配模型Fig.16 FEM model of aircraft fuselage panel assembly
图17展示了A板以定位点、铆接点为约束点进行曲面修改得到的逼近模型。图18所示为逼近模型、理论数模与实际数模对应的装配分析结果沿Z轴的分量。

图17 壁板件拉普拉斯逼近模型Fig.17 Aircraft panel Laplacian deformation model
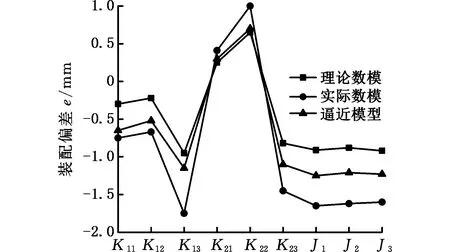
图18 Z向装配偏差分析Fig.18 Deviation comparison in Z direction

图19 壁板件上新增约束点Fig.19 Add constraint points on fuselage panel
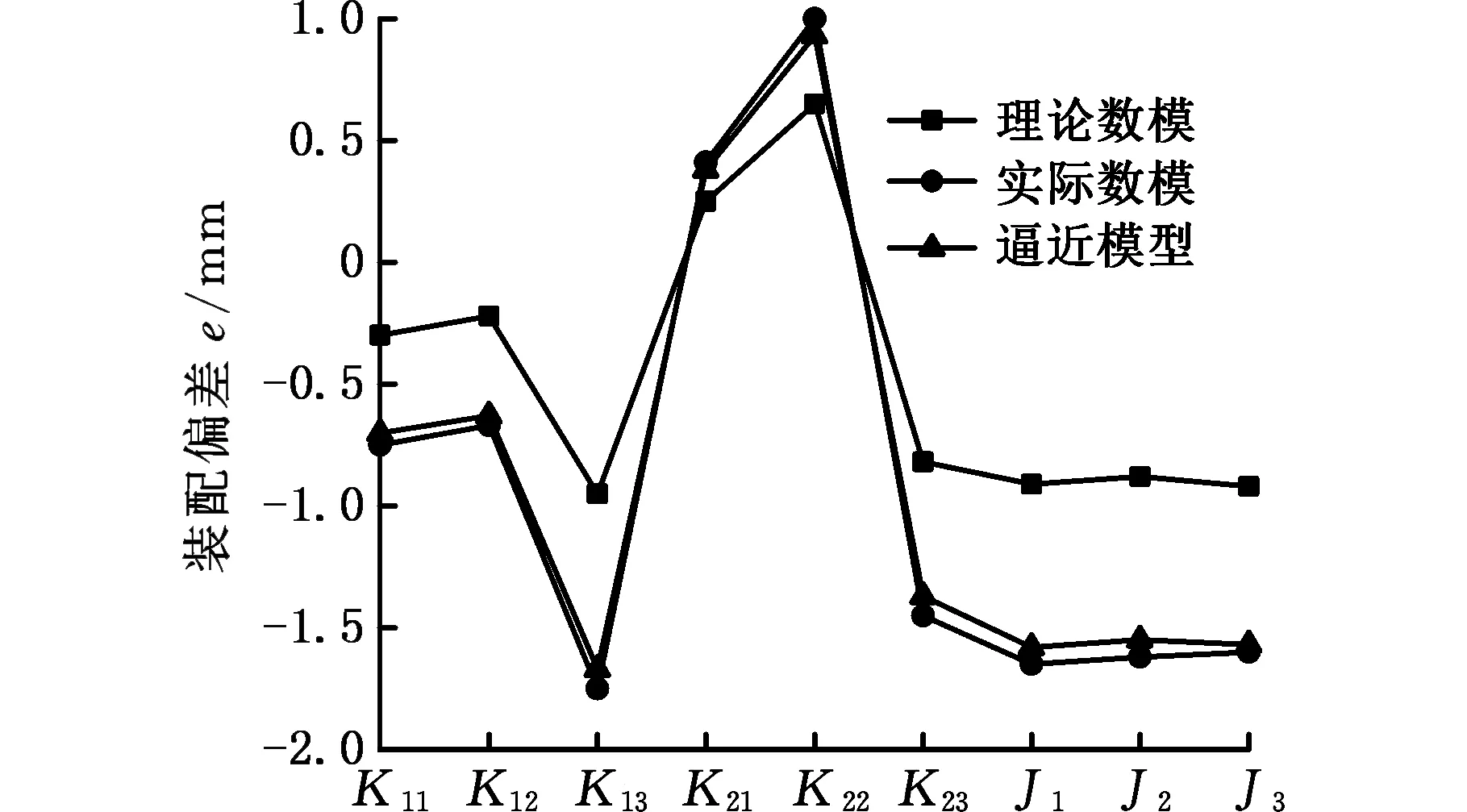
图20 Z向装配偏差分析(增加约束点)Fig.20 Deviation comparison in Z direction(add constraint points)
理论上,为进一步提高本文方法分析的准确性,拉普拉斯变形中可给定更多的约束点,确保修改后曲面形状(逼近模型)更加贴近产品的实际外形,图19演示了新增的点约束。图20所示为新的装配偏差分析结果对比。在图20中,由逼近模型计算得到的装配偏差分析误差减小到5%以内,装配偏差分析准确性得到了显著的提高。
5 结论
(1)本文提出一种柔性件装配偏差分析改进方法。使用误差源和理论外形,结合拉普拉斯矢量得到逼近实际外形的曲面外形,并采用逼近外形对应的敏感度矩阵进行装配偏差分析。
(2)通过金属薄板装配和飞机壁板件装配试验获取各类偏差数据并进行对比,结果表明改进方法可使传统的分析误差率减小到5%以内。本文研究为提高飞机装配偏差分析准确性提供了有效补充手段。
