论运动的绝对性
2019-10-25咸立德
咸立德
(曲阜市书画社,山东 曲阜 273100)
本文从时钟具有物质性的角度,论述了不同的时钟受运动的影响程度的不同性,不同的时钟意味着不同的时间流动速度,意味着,时间必须依靠物质性时钟来获取,表面上看,时间就相对的,而依据《自由运动论》所描述的运动规律,是在内力作用下,以原始质量虚空中心为参考的运动,宏观相对静止参考也是不能任意选择的,所以,在内力作用下的自由运动具有绝对性。时间的物质性定义只能说是导致理论的不准确性的因素,不准确性和相对性有本质的区别。本为论证了相对性仍然是一种误差较大的一种绝对性形式的关系。
一、时间与时钟的关系
《试论光速不变现象的成因》一文,只从实验结构上论述了实验设定距离的可变性对光速检测结果的影响。事实上,实验中的时钟因受运动的影响也是影响光速的因素之一。
从物理性上来考虑,依赖于具有物质性的时钟来等效于时间,会存在时钟性能因运动而不同,时间也就会有因时钟的不同而不同的性质。而且不同的时钟在运动中所受影响的程度也是不同的。比如,古老的沙漏计时器,其原理是利用了沙这种固体物质的自由落体现象,沙漏速度等效于时间的流动速度,但是,当把沙漏计时器连同观察者的观察系统做自由落体,或者加速到太空做自由运动时,沙就会在自由运动中停止沙漏现象,那么,沙漏停止,就意味着时间的停止,即沙漏这个计时器还没达到很大的速度,时间就会停止。当再给自由落体加速,沙漏现象就会向相反方向上流动,等效为时间在倒流。如图1(a).

又比如日晷计时器,静止在地面,在地面有个自西向东的线速度v的前提下,时间t是用晷针的投影的移动等性质定义为常规时间的流动,当给日晷一个自东向西的一个速度v1,使v1=v,则投影停止移动,相当于时间t1停止。再加速为v2,即v2>v时,投影就会向反方向移动,相当于时间t2在倒流,如图1(b)。
时钟具有物质性,时钟因运动而改变性质也是客观存在的,而且存在计时器所利用的计时原理以及计时载体(比如沙漏计时器中的沙粒)的质量(或者密度)越大,受运动的影响程度越大。所以,并不是任何形式的时钟受运动的影响程度都是相同的,比如,沙漏计时器,时间在很小的运动速度上就会停止,而十分精确的电子计时器、原子钟等,因为利用了质量极小的电子当做计时载体,几乎在光速时才会停止。
计时器原理不同时,时间受运动影响的性质是不同的,比如沙漏计时器在加速后可以减慢,而日晷相反,从地球的自转方向来考虑,自西向东高速运动等同加速,而自东向西高速运动等效为减小运动速度。而日晷计时器在自东向西做减速运动时,时间反而是加速的。
以上分析说明,物理理论用宏观时钟作为计时工具来定义时间具有局限性,理论上时间不能等同于时钟。但在科学必须具有可实证的前提下,必须用时钟定义时间的存在性,但会影响理论的准确性。意味着,寻找受运动影响更小的计时载体也属于科学的研究方向。
二、光速可变性在时空中的作用
(一)匀速运动状态中的时空。依据现代科学,事件是以光速向外传播,在二维空间中,无论事件运动与否,因为光速具有不变性,二维空间的传播可用正圆来描述,但是在光速可变的前提下,运动事件的传播就不是正圆,而是椭圆,如图2(a)所示。
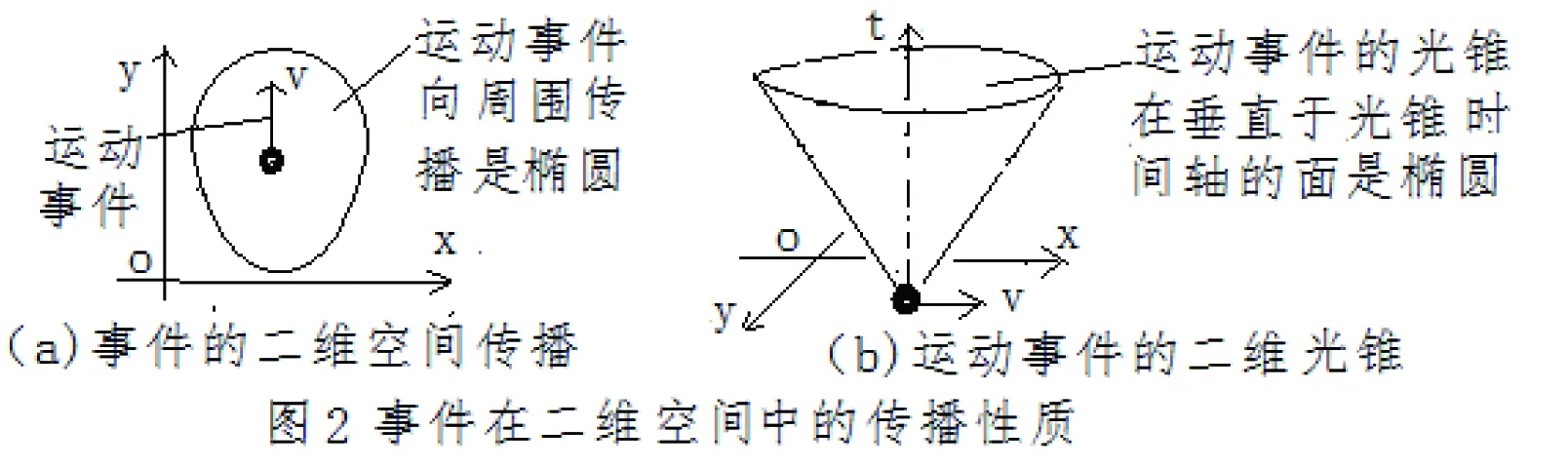
在三维时空(二维空间加一维时间)中,事件的传播可用光锥来描述。但根据光速的可变性,当事件有个运动速度v时,光锥因为光速的可变性具有不对称性。即垂直于时间轴的截面不是圆,而是椭圆,如图2(b)。
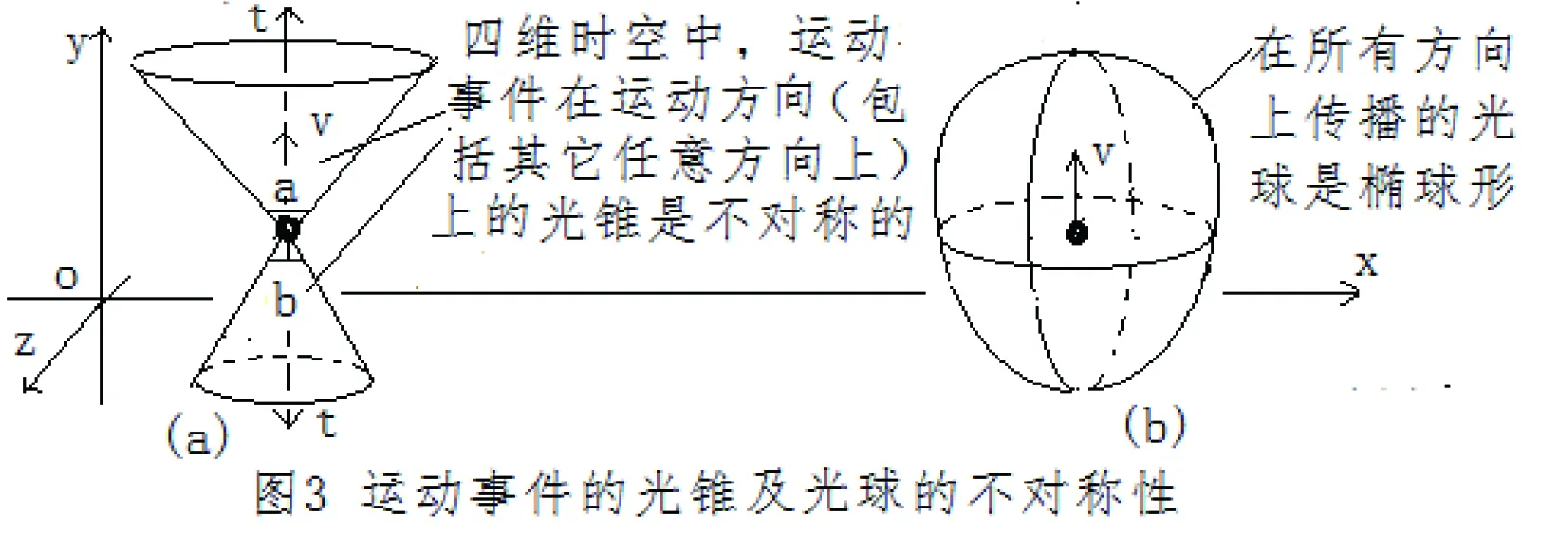
同理,在四维时空中,运动的事件在运动方向上(包括所有方向上)的光锥是不对称的光锥,有∠a>∠b,如图3(a)所示。
在无限维度上,事件向周围无限维度上传播,可视为以事件为顶点,由无限个时间轴上(或者无限个空间方向)的光锥构成的光球。运动的事件的光球是椭球形,如图3(b).
图2、图3是不考虑曲率运动问题,从不同时空维度描述运动事件的光速传播性质,在光速可变性的基础上形成的不对称的性质,事件处于椭圆中心。但在考虑事件在内力影响下的曲率运动性质时,运动事件是椭圆(或者椭球)的焦点,如图4所示。

时空中的光锥的不对称性质,与考虑粒子曲率运动的轨道具有椭圆性质,光粒子在大尺度上也具有椭圆公转性质是一致的,与宇宙的非对称性也是一致的。
三、光锥性质分析
(一)对于事件的理解。本文可理解为事件具有物质性,存在发生和事件在发生之后的物质运动规律的描述。比如,两粒子发生碰撞视为事件,事件就不仅仅只包含碰撞过程这个事件点的发生,而在碰撞之后的粒子的运动情况也属于事件的部分。
(二)事件的过去和未来的性质。事件在三维时空中用光锥表达,对于事件本身和其他观察者而言,光锥的过去和未来的性质是不同的,对不同观察者而言光锥具有不同的过去和将来的区域性,比如,对于远处的观察者来说,光锥可分为未来光锥和过去光锥两部分,如图5。
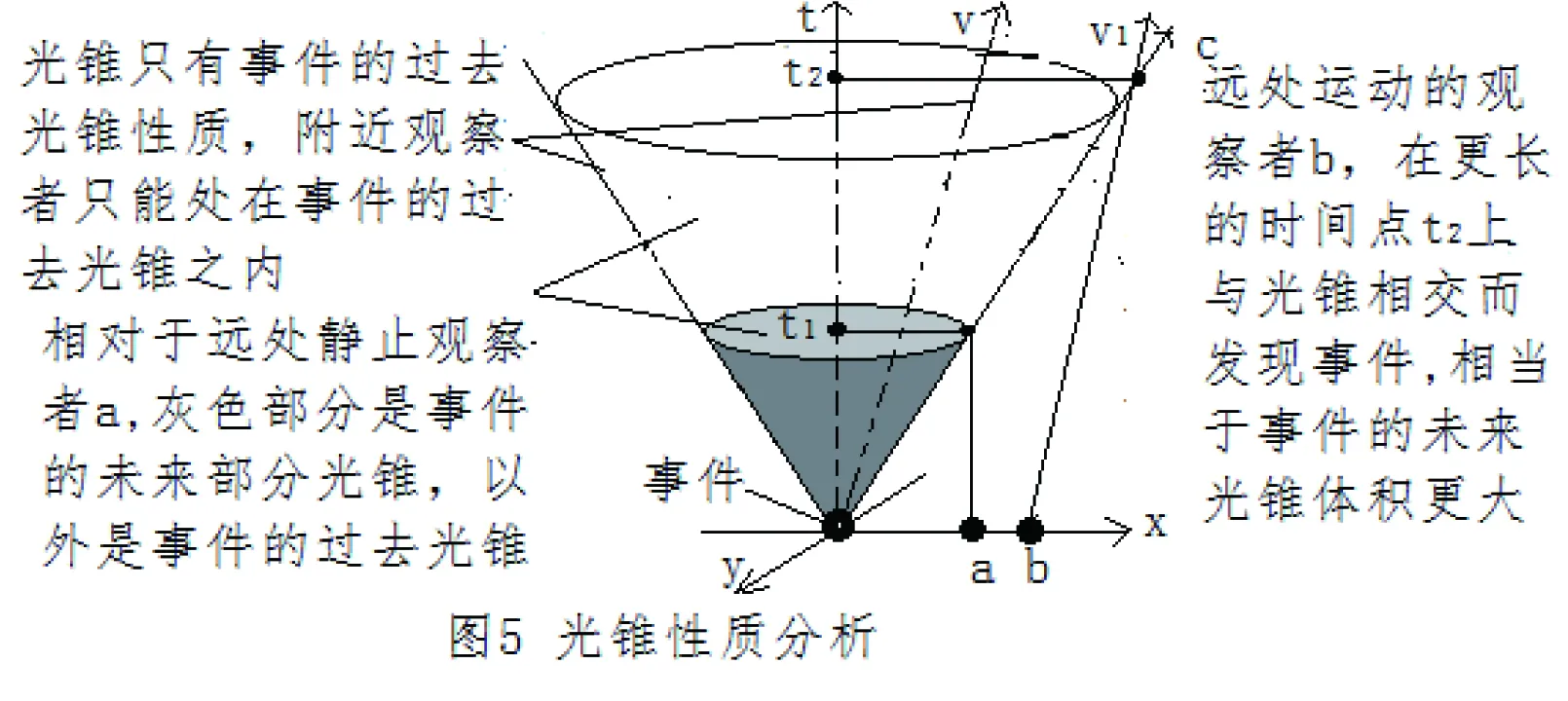
远处静止的观察者a由于与事件之间存在距离而存在对与事件观察的延时性,其延时时间为t1,t2以内的灰色部分对于观察者a就是事件的未来。以外事件所能传递到且已经到达的任何距离上的光锥部分都属于事件的过去光锥。
对于远处的运动者b,延时时间t2因为运动而增大,且有∠1>∠2。未来光锥属于t2以内的部分,以外事件到达的部分是对于b的过去光锥。
对于事件附近的观察者,和事件之间的距离忽略不计,对于观察者来说,事件只有过去光锥性质。
对于事件本身,未来光锥属于在无限的时间内尚未到达的可预测部分。过去光锥是已经传播的时间内的可观察的部分。所以对于事件本身,光锥的未来和过去的性质和对于远处观察者来说是不同的,如图6(a)。
设事件在传播时间为t0,则t0以内的圆锥0ab是事件的已发生的过去光锥,以外尚未到达的可预测的无限时间t部分属于事件的未来光锥。
对于过去概念的定义或者说理解,还可以包括事件发生以前的性质。但逻辑上讲,所谓事件是指事件已经发生的问题,在无限小的时间段内产生无限小的过去光锥,而对于事件发生之前的过去,理论上应该属于另一个事件的问题,可以理解为,一个事件a是另一个事件b的转折点。所以一个事件是建立在前一个事件光锥之上,如图6(b)所示。
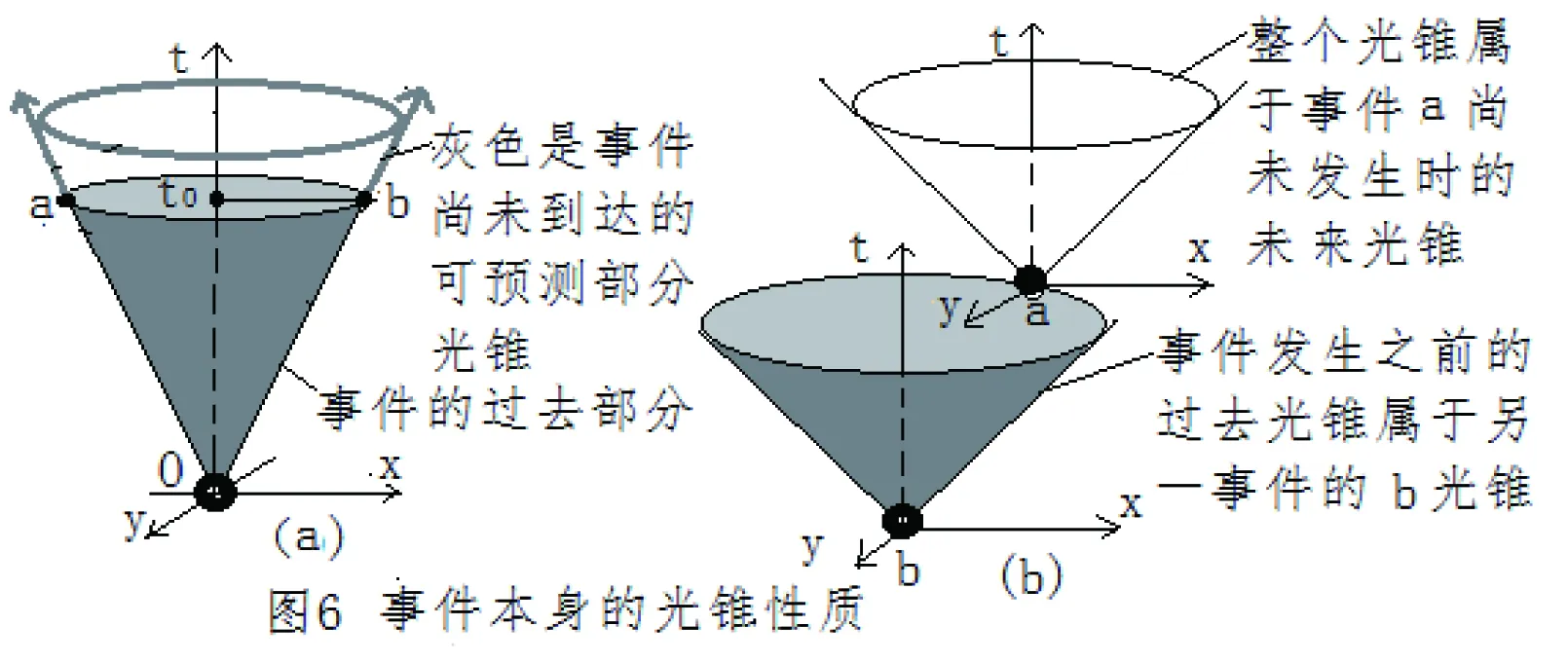
也就是说,事件的光锥的未来和过去的性质,相对于事件本身和傍观者是有所区别的。
四、不同维度的曲率运动的等效性
低维度上的曲率运动是相对于低维度的虚空中心的运动,为了便于比较复杂运动系中的独立天体之间绝对运动。可以等效性的展开转化为更高维度的曲率运动的形式。如图7。
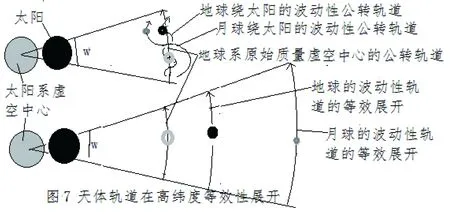
以地球系为例,地球和月球都是绕着地球系的原始质量所在的虚空中心公转,此时可视为一维公转,在考虑绕太阳的二维波动性公转性质时,可以把地球及其月球的二维波动轨迹等效性的展开来考虑问题,此时,相当于地球和月球的二维轨道就转化为圆滑的弧形轨道了,而且存月球绕太阳的公转轨道半径要大于地球的轨道半径,因为展开后绕太阳的公转角速度仍然是相同的。所以,月球的公转(运动)速度要绝对性的大于地球的公转速度。表明,地球和月球的运动速度因为质量(或者密度等)的不同而存在速度的绝对不同性。
以此类推,也可以把太阳系的公转考虑在内,来等效性的把各大天体的轨道等效性展开,来对比太阳系中的所有天体运动速度的绝对性。
曲率运动的等效性展开也是适用于微观的,以及整个宇宙的,比如在《自由运动论》中所描述的光速不变一样,把构成物质的最小的光粒子在复粒子中的运动轨迹在更高维度的太阳系展开,光粒子也具有太阳系中的公转性质的光粒子的性质。也就是说,光粒子在自转速度和运动速度许可范围内(不因运动速度增大继续分裂成更小的微粒子),在哪个维度上的运动速度(速率),是基本相同的,都在光速范围之内。运动速度的绝对性是质量(密度)具有绝对性且和运动速度成反比所决定的。
五、曲率运动对时间的影响
图7所描述的原理,是更便于比较各个天体之间的绝对运动性,同理,其它的行星等都相对于太阳系虚空中心有绝对性的运动。比如看起来公转轨道速度慢的气态行星,那是因为在自己系里的一维公转轨道半径大(轨道半径大即表现为气态星系的密度小),但把二维波动轨道等效性展开为二维弧形轨道时,轨道半径就会急剧增大,此时二维运动速度显示为很大。所以,在太阳系里,各大行星可以视为轨道半径越大的,运动速度也越大的性质。
一般的,把极近中心的太阳视为太阳系的中心时,太阳可视为相对静止的,观察太阳发生的事件时,在公转的各大行星上的延时时间是不同的。外轨道上的延时时间会大于内轨道上的延时时间。如图8所示。
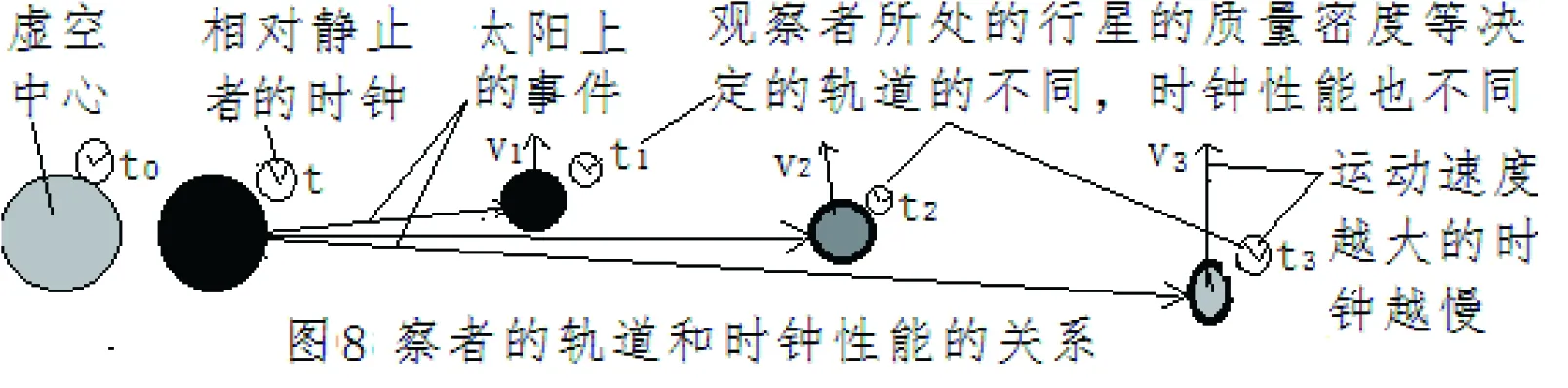
虽然其他行星的曲率运动相对于太阳并不存在相互远离的运动。但由于轨道的不同运动速度的不同,各自的时钟仍然会因为运动速度的不同而不同。在曲率运动中可以用公转角速度来描述相对运动,所以,严格来讲,影响时钟的是速率。
如果科学必须用物质性的时钟来作为获取时间的工具,而时钟会因为运动速度的增大而减慢,即同样的时钟在外轨道上时要减慢,有v1 虽然天体的速度不同导致时间不同,但是由于天体的曲率运动(轨道偏心率忽略),天体和太阳的距离可视为不变的,即,天体和太阳之间并不存在相互远离(或者靠近)的相对速度,而事件的延时性基本与距离有关,所以太阳的事件在天体上的延时时间是不变的。但同时考虑时间不同时,时间的不同会影响延时时间的准确性。即时间减慢会缩小延时时间。 若时钟的性能存在因为轨道的增大而减慢,恰好抵消了各个天体轨道的增大而延时时间的增大,甚至导致了不论在哪个轨道上都会同时观察到太阳上的事件。 以上分析可知,科学理论,不能仅仅停留在纯理论的描述上时,在事实观测的过程中,理论的准确性与时钟的性能有直接关系。意味着,时钟从原理性以及计时载体的选择上,受运动影响程度越小,观测和理论的吻合程度越大。 (一)绝对静止虚空中心参考的存在性。按照《自由运动论》的理论,天体存在一个虚空中心,一个星系也必定存在一个原始质量的虚空中心,以此类推,宇宙也必须存在一个虚空中心,这个虚空中心可定义为绝对性的时空中心。即所谓的物质的运动曲率是相对虚空中心的曲率,曲率与物质质量等物理量之间具有绝对性关系,在描述物质运动的所有物理量都具有绝对性,轨道所决定的物质性能是不变的。意味着,不存在不改变天体的内部性质(自转速度,运动速度以及密度等)就能够随意的改变相对虚空中心的运动曲率。 按照《自由运动论》的理论,时间和空间在以虚空中心为原点的坐标系里,在无限维度上无限延伸,包括在不可视空间中无限延伸。之所以存在不可视空间,正是因为物质在内力作用下做自由曲率运动,包括被假设的质量最小的光粒子的运动也具有绕光源公转的性质。所以,在人类仍然依靠光作为观察工具的前提下。在光粒子可达到空间以外就可以定义为不可视空间。 所谓的粒子的自由运动曲率运动,是相对于虚空中心的,粒子一维曲率运动是相对于一维虚空中心的,当考虑到二维运动时,一维虚空中心可视为随同粒子的运动而运动。但以此连续叠加,理论上总存在整个可视空间的物质的虚空中心。所有物质粒子的虚空中心可视为绝对静止的虚空中心。也就是说,粒子在局部空间中的低维度的曲率运动的系统中心是相对静止的,但整个可视空间的粒子的曲率运动的虚空中心可以理解为绝对静止的。如图9。 当on(xnynzn)代表了整个可视空间的虚空中心时,就是绝对静止的。就像真空的存在性一样具有极端性质。比如,相对于所有的观察者光速都是相同的,而且在真空中,光速是恒定的。所谓的所有观察者,无非就是描述了所有不同粒子的运动,包括粒子在无限维度上的叠加之后的运动,所有观察者的叠加可视为整个可视空间的物质的整体性。而真空无非也是理想的不可观测的存在,所以,真空可以等效为极端的绝对静止的不可测的参考。如果科学不允许不可测的真空的存在,那么所谓的真空中的光速就是没有依据的。 局部空间的粒子的虚空中心,以及粒子高维度曲率运动的虚空中心,都是依据粒子的曲率运动而存在,曲率运动以虚空中心而存在,也就是说虚空中心和曲率运动是并列相对存在的,是相互依存在的。所以,逻辑上,如果把不可视空间,包括粒子虚空中心定义为不可测性是不合乎逻辑的。粒子的可观测性完全可以等效为虚空中心的可测性。比如,不考虑两个天体之间空间微粒子的存在,视为真空,那么两个的天体之间的空间本属于不可测的真空,但是,完全可以依据两个可测的天体的存在来确定天体之间的不可测的真空空间客观存在性。是说,天体的客观存在反过来证明了不可测的真空的存在性。 另一方面,从图7描述的原理出发,当把所有局部性的天体(粒子)的曲率运动都等效性的展开,所谓的低维度的虚空中心也没必要考虑随着天体的运动而运动的性质了,此时的性质相当于一个静止轨道的参考,就像天体的运动轨道,只是一个不具有运动性质的天体运动的可预测轨迹一样。所以,从图7描述的原理可以更容易理解虚空中心客观性,以及可以把相对静止转化为绝对静止的性质。所以,以此类推,把所有的天体都等效性展开来考虑,图9所描述的绝对静止的虚空中心的客观性就更明确。也就是说,虚空中心作为静止参考的客观性,等同于天体运动轨道也具有可预测而且不具有运动性质的客观性。 以上分析表明,相对静止参考包括极端性的绝对静止参考是客观存在的,与粒子的曲率运动是相互依存的。把虚空中心视为粒子运动的静止性参考也是具有可预测性的。也就是说,《自由运动论》把虚空中心视为粒子的曲率运动的绝对性静止参考具有可预测的客观性。 (二)相对静止参考的正确选择。事件是由物质构成,即事件具有物质性,而观察事件的工具仍然可以依赖于物质性的光粒子的运动。那么,事件必须具有宏观的物质性,把不具有物质性的虚空中心视为静止的参照,可以更准确描述物质运动规律。而对于事件的描述,由于事件具有物质的属性,习惯于把某个可观察天体当做相对静止的参照是科学观察的需要。所以,一般都以极近虚空中心的中心天体作为相对静止的参考(早期的科学甚至认为是绝对静止的)。但以物质性的中心天体当做相对静止的参考时,自由运动曲率公式在应用中必将存在不小的误差。相对于当前的科学,自由运动曲率的区别就在于,同时考虑了原始质量这个虚空中心的存在性。 由第三、第四的论述可知,相对于虚空中心,运动具有绝对性,存在极近虚空中心的天体具有质量大运动速度最小的性质。即便是在科学需要的前提下,必须选择宏观的物质性的时钟获取相对时间,以及宏观的粒子作为相对静止参考来考虑运动的规律性时。相对静止的参考也不宜随意选择,选择极近虚空中心的天体作为相对静止的参照是更合乎逻辑、更符合客观规律的。《自由运动论》不允许宏观的相对静止参考的随意选择及其互换。只有正确的选择相对静止的参照,才能够更容易、更准确的描述事件的规律性。 时间必须依赖于物质性的时钟来定义,表面上运动相对于可变的时间具有相对性,但是根据不同的时钟受运动的影响程度的不同姓,相对运动也会因为时钟的不同而不同,同时考虑这个问题时,相对运动会变得更复杂。 另一方面,既然不同的时钟受运动的影响程度是不同的,就存在什么样的时钟更准确,受运动影响程度更小的问题,这个问题意味着,必须存在一个绝对的时间作为参考,才能够比较时钟的准确性。也就是说,相对性也会因为时钟的精确与否影响到相对性的准确性。从这个角度来考虑,根据第五节的论述,用时间的可变性建立运动的相对性是多余的,而且同时存在以宏观粒子作为相对静止的参考,而且可以互换,会产生极大的不准确性。相对运动性最终会归结为绝度性中的不准确性。 也就是说,科学理论必须用物质性的时钟来定义时间,只能说时间的可变性会导致理论具有不准确性。这和事件的随机性也是绝对性的一种形式一样,相对性也必将是误差较大的绝对性的一种形式。因为科学在具有实证性的前提下,观测工具的物质性限制了理论的准确性,用时钟定义时间,用有限的观测工具观测微粒子的行为,导致运动具有相对性及微粒子具有随机性的错误结论。所以科学所依据的可实证性形成的理论误差可视为不准确性是比较理智的。 (一)时间的主观性。从科学的角度来考虑,必须建立坐标系来描述宇宙的运动规律,包括时间可以定义为与空间相互垂直的方向,在二维时空中尤其性质突出,但宇宙物质运动毕竟是多维的。在多维的空间中建立多维的时间轴,时间轴也就存在具有在所有方向上延伸的性质。 从另一角度考虑,图6(b)描述的事件的转折性,也可理解为事件是可以按不同的方向变化的,比如,事件a可视为两个质量较小的粒子发生纠缠性碰撞形成复粒子的事件,那么所谓的事件的发生到事件在无限时间上延续,其事件a的光锥就是一个复粒子的运动情形。而事件a的过去光锥是另一个事件b的运动情形,即相当于纠缠性碰撞之前的两个粒子的运动情形。 事件可以反过来发生,可以是一个复粒子在发生湮灭性碰撞时,一个复粒子在碰撞之后分裂成两个更小粒子的运动,所谓事件a就是湮灭性碰撞,光锥就是湮灭性碰撞之后的两个粒子的运动情形,而事件a的过去光锥就是发生湮灭性碰撞前的复粒子运动情形。 粒子之间即存在湮灭性碰撞之后的运动系统的膨胀,也存在纠缠性碰撞的运动系统的收缩。如果把膨胀事件中的时间视为时间的流动方向,那么收缩事件中的事件中的时间相当于反方向流动。所以,就像系统的熵一样,既有向着熵增方向发展,也可以存在向熵减方向发展。即,时间不可以定义为具有严格特定的方向。同时考虑物质的曲率运动,时间随之具有循环性。所谓时间的无限性是在循环中具有无限性。只是描述物质运动的一个物理标量。 从整个宇宙的时间性质来考虑,第一,宇宙即不必要纠结起源于某次唯一膨胀,第二也不必要纠结是否起源于所有微粒子的收缩,第三,宇宙是在多个膨胀及收缩的无限循环状态之中。即宇宙没必要纠结起源于所有微粒子的纠缠性碰撞逐渐形成较大的不同的宏观天体,也没必要纠结是否起源于某个唯一的宏观天体的的膨胀才形成了微观世界。宇宙可以按《自由运动论》所描述的,宇宙是在变化中守恒的。即便是三者情况都视为有可能存在,那么第一和第二种情况,在宇宙的演化中,也必将仍然会遵循《自由运动论》所描述的运动规律运动,即宇宙无论以什么情况作为起源,都必将是相对一个绝对静止的虚空中心作为参考的绝对性曲率运动形式。 综合分析,客观规律并没有赋予人类关于时间的存在性,只是人类依据客观物质具有变化性定义了时间的存在性,时间是人类的主观定义,时钟更是人类的主观产物。 (二)时间的不对称性。在《宇宙非对称性及能量守恒原理》一文中,从粒子的纠缠性以及严密性碰撞性质不同的角度,论述了相互作用时间的不对称性,这种不对称性对于事件的三维时空光锥的性质也是有影响的,如图10所示。 图10中的光锥x、y、t1中灰色部分,t是粒子碰撞时相互作用到形成复粒子时所需要的时间。而光锥x、y、t2中的t′,是粒子碰撞时相互作用到裂变成更小粒子时所需要的时间。是理想的发生纠缠碰撞形成复粒子的反过程。 质量相同的两个粒子的湮灭性碰撞中的相互作用力大于纠缠性碰撞中的相互作用力,由于相互作用力和作用时间成反比,所以存在:t>t′。 时间的不对称性,在粒子之间不具有形成复粒子的纠缠性碰撞及湮灭性碰撞中也未必导致裂变为更小的粒子的情况中,只是导致了相互作用之后的运动性质发生变化,导致运动速的增大或者减小时,其过程中的相互作用时间也是不相同的,具有不对称性。 (三)加速运动对三维时空光锥的影响。事件的发生需要一定的时间,事件发生后,其能量转换也是具有延时性质的,粒子的运动在延时时间内具有加速性质,依据光速可变性对光锥的影响,加速中的光锥面不是平直的,而是锥面凸起或者锥面凹陷的光锥,如图11所示。 图11(a)所描述的粒子在纠缠性碰撞事件a中(包括没有形成复粒子的纠缠性碰撞),导致粒子自转速度增大而运动速度减小时,从界面相互作用到作用之后的动能转化为自转能的延时时间t内,显示为减速性质,由于减速对光速的影响,在粒子运动方向上,光锥面就有类似酒杯的凸起性质。相反,在图11(b)所描述的粒子在湮灭性碰撞事件b中,导致粒子自转速度减小而动能增大,从相互作用到相互作用之后的自转能转化为动能的延时时间t′内,具有加速性质,其光锥面就有类似喇叭的凹陷性质的锥面。 在t、t′以外的无限时间t1、t2上粒子进入匀速运动状态时的光锥部分的锥面就有平直性质。如果把粒子进入匀速运动状态视为另一事件的开始,那么,深灰色光锥可视为粒子在匀速状态中的运动方向上的光锥,而且有:顶角∠1<顶角∠2。 结合上一节的论述,图10是没考虑相互作用中加速运动对光锥锥面的影响,图10中的灰色部分要包含于图11中的灰色部分之内。意味着,图11中也存在t>t′的性质。也就是说,在粒子相互作用的理想的反过程中,在能量守恒的延时时间内,时间是不对称的。 (四)时间的平直性,以上分析表明,时间在相互作用的理想的反过程中是不对称的,时间的不对称性不影响时空的平直的特性。这种不对称性是第三观察者对于粒子的相互作用及其反过程的性质的观测,是第三观测者的时间,这里并没考虑相互作用的粒子自身的时间在相互作用后速度发生变化的影响。所以,时间的不对称性和时间受运动影响的可变性是有区别的。图10、图11所描述的时间轴的量度是相同的。不影响时间的平直性。 当考虑到事件本身(观察者)的时间因运动而受影响时,时间轴仍然是平直性质,所谓运动速度的不同时间的不同,可以等效为时间轴的量度的不同,也是不影响时间轴的平直性。 另一方面,时间在不同的观察者的坐标系中度量不同,可视为时间的可变性,但这种可变性也并不能恰好抵消光速的可变性来等效为光速具有不变性。如图12所示。 图12中,不同事件的光锥可以同时视为不同的运动观测者及其光源,且有,在运动方向上,运动观察者(b)的光速c2会增大,有c1 结合第五节的论述,理论上的时间和空间一样,具有平直的性质,是在所有方向上的无限延伸。表明《自由运动论》时空框架是平直的。用时种定义时间会给理论带来的误差,不影响时间的平直特性。所谓的绝对静止参考系,是指时空的平直参考系,粒子在内力作用下的曲率运动,是相对于这个平直时空的曲率运动。 科学的特性在于,科学必须具有实证性,这就意味着,任何物理量都必须存在物质性,只有物质性才可以具有可观察可实证的性质,所以,比如时间这个物理量,如果不借助于物质性的计时器,就无法实证。借助于物质性的计时器,就会受运动的影响而不准确。所以人力无法扑捉绝对不变的时间,所有的物理公式、方程都必将存在误差。 从逻辑上来考虑,只有从纯理论性的角度来想象宇宙的运动规律,即时间具有不受任何运动的影响的理想状态下,理论才能够绝对准确。所以,执着于可实证性的科学理论,只能意味着理论永远不会绝对准确的描述客观规律。 客观规律与人类是否观测无关。所以,在科学的规范中,不观测,宇宙仍然按规律运动着。若观测,就会因为观测工具的物质性而不准确。比如,用光锥描述物理规律时,时间轴是理想的绝对时间,理论就绝对正确,当时间轴在实际应用中用时钟所代替,理论就会出现误差。所以,科学理论必须具有实证性时,就必须处于存在误差的境地之中,而且会因为必须实证时的观测工具的局限性,会出现类似相对性及其随机性的理论性的错误。 用物质性的时钟定义时间,不同的时钟受运动的影响程度是不同的,用相对性描述运动会变得更复杂,而且以宏观的物体作为相对静止运动的参考,甚至可以互换参考,是及其不准确的,或者无意义的。只有在内力作用下,以绝对静止的虚空中心做自由曲率运动的参考,粒子运动具有绝对性的角度来描述运动规律,才能够更符合客观规律。时间受运动的影响,可视为对运动规律产生误差,导致了运动规律具有不准确性的因素。从逻辑上来讲,相对性仍然可归类于误差较大的绝对性的一种形式。六、绝对静止参考的客观性

七、相对性和不准确性的关系
八、时间的本性
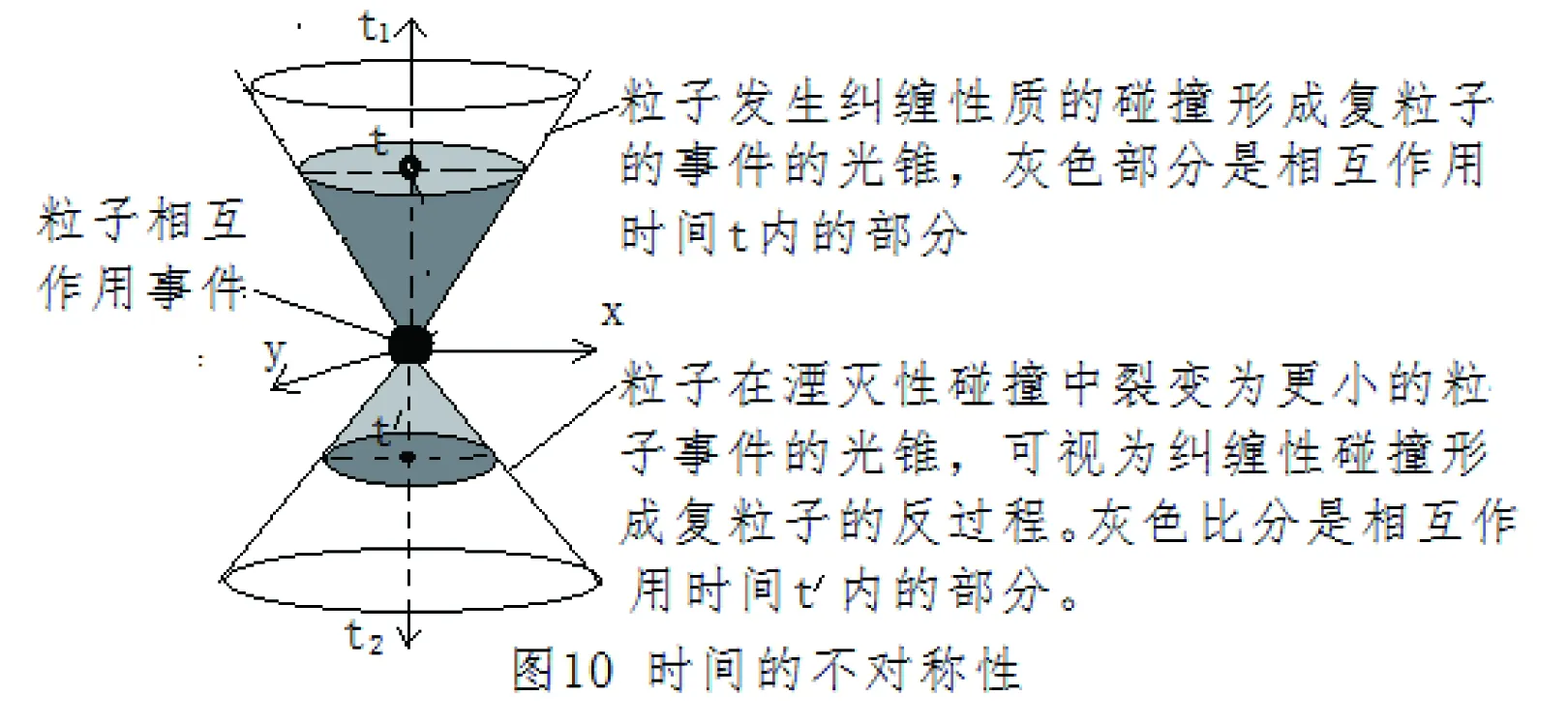
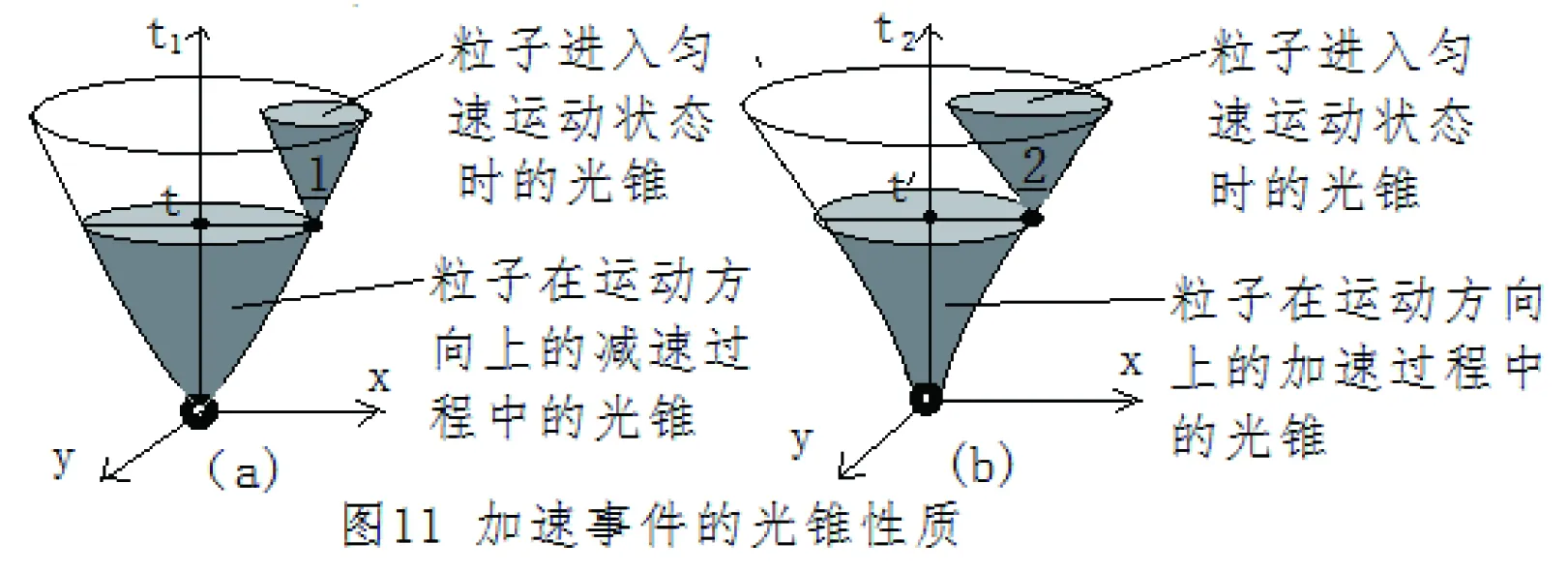
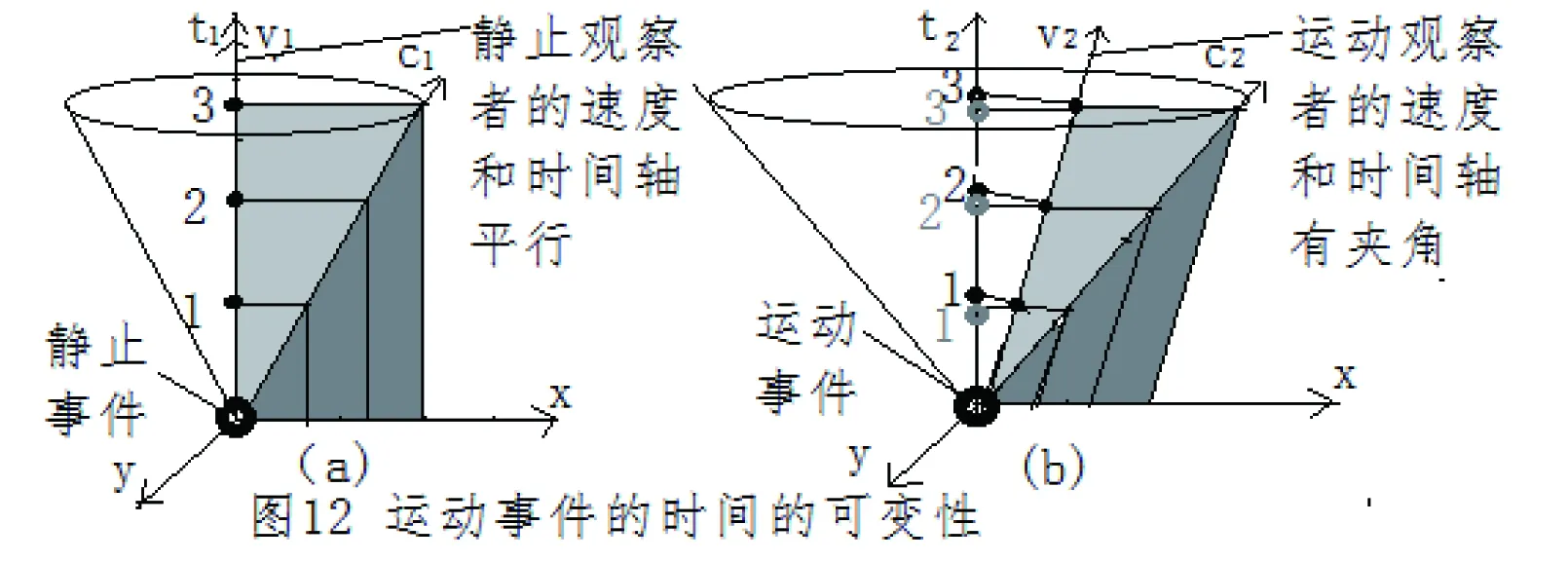
九、科学理论的局限性
十、结论
