阀门填料密封设计研究

刘海杰 田瑞青

(东方电气集团东方汽轮机有限公司，四川618000)

阀门密封始终是阀门设计中关注的问题。由于需要实现阀门的“零泄漏”，因此选用了可适用于高温高压环境下的石墨填料密封。

国内外对填料密封均作了大量研究分析，刘兴玉、郝木明等人[1-2]对填料进行了理论分析，研究了填料的压力分布规律，其中郝木明对石墨填料进行微元分析，得出了侧压系数的计算公式；宋鹏云、肖光凯等人[3-4]分别对填料分析中侧压因数进行理论分析和试验研究，励行根等人[5]对柔性石墨填料密封性能进行了研究，重点通过试验比较了平口和V口组合填料的摩擦力和泄漏率的不同，蔡仁良[6]在其著作中提到了国外作者W. Ochonski提出的软填料的压缩率计算公式，洪小飞等人[7]提出了高参数阀门泄漏问题的维修更改方法。以上这些均对本次填料密封的设计提供了非常有益的指导。

1 填料密封的结构

填料密封是用填料填塞泄漏通道，阻止泄漏的一种密封形式。填料密封结构简单，常见结构如图1所示。密封原理从理论上讲就是填料对阀杆的压力大于工质压力；从机理上讲，主要是“轴承效应”和“迷宫效应”。轴承效应即是填料与阀杆挤压，由于石墨具有压缩性和润滑性，所以填料与阀杆的情况类似转子与轴承，二者之间充满润滑剂，既可以相对运动，也具有密封作用。迷宫效应，即是由于阀杆表面光洁度原因，石墨填料和阀杆只是部分贴合，部分留有间隙，再加上各级填料环的存在，这些间隙基本相互隔断，类似迷宫带，对气流有节流降压作用。

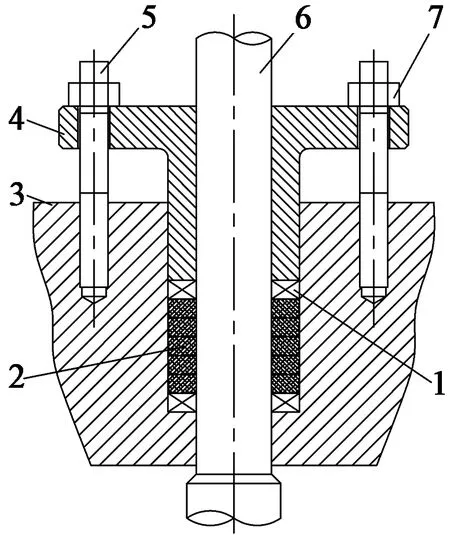
1—编织填料 2—膨胀石墨填料 3—填料压盖 4—压盖法兰 5—压盖螺栓 6—阀杆 7—压盖螺母 图1 阀门填料密封结构Figure 1 Structure of valve stuffing seal

2 阀门填料密封计算分析

2.1 压力分布计算

根据密封原理得知填料受压，自身产生轴向压应力，从而挤压阀杆，和阀杆之间产生压应力。当此压应力大于工质压力即可密封。按照图1常用的密封结构对填料受力进行分析，见图2。设轴向压力为Py，对y处的填料微元进行受力分析，得出微元方程：

π(D2-d2)Py4=πdμ1Px1dy+πDμ2Px2dy+

π(D2-d2)(Py+dPy)4

(1)

式中，μ1、μ2分别为填料和阀杆、填料函(阀盖)的静摩擦系数，d为阀杆直径，D为填料函直径。填料和阀杆、填料函(阀盖)的径向应力分别为Px1、Px2：

Px1=K1Py，Px2=K2Py

(2)

式中，K1、K2分别为填料和阀杆、填料函(阀盖)的侧压系数，即径向压力与轴向压力的比值。

由上式(1)和(2)，整理可得：

Py=Py0e-βy

(3)

Px1=K1Py0e-βy

(4)

Px2=K2Py0e-βy

(5)

由(3)～(5)式得出：

从以上三式可以看出轴向填料轴向应力和径向应力的分布情况，如图3所示，沿y向呈指数分布，逐渐减小。当y=h时，有Pxh=工质压力P0，则此处为密封临界点，y≤h为密封有效区域，h称为有效密封长度。H-h区域为密封失效区。因此设计时须控制无效密封长度，否则增大摩擦力，对密封无多大意义。但一般来说会有一些密封裕量，即允许存在少量的无效密封区。

1—阀杆 2—填料 3—填料函(阀盖)图2 填料密封受力分析Figure 2 Force analysis on stuffing seal

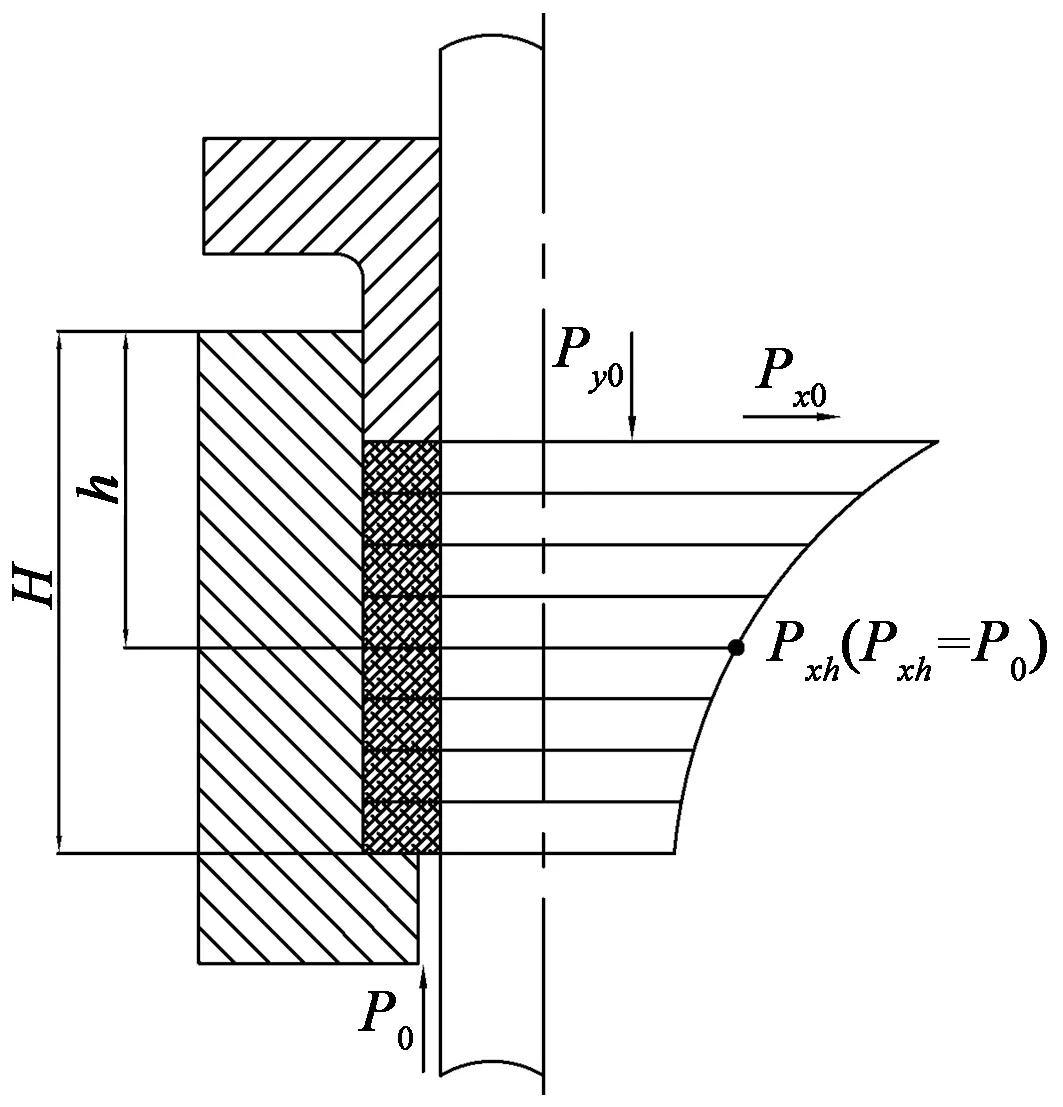
图3 填料压力分布
Figure 3 Distribution of stuffing pressure

2.2 侧压系数

文献[3]通过理论分析得出侧压系数K1、K2的理论关系，如下：

(6)

侧压系数的确定都是通过试验测定的，比如文献[4]即通过试验测定了不同轴向压力下的侧压系数，如图4所示。

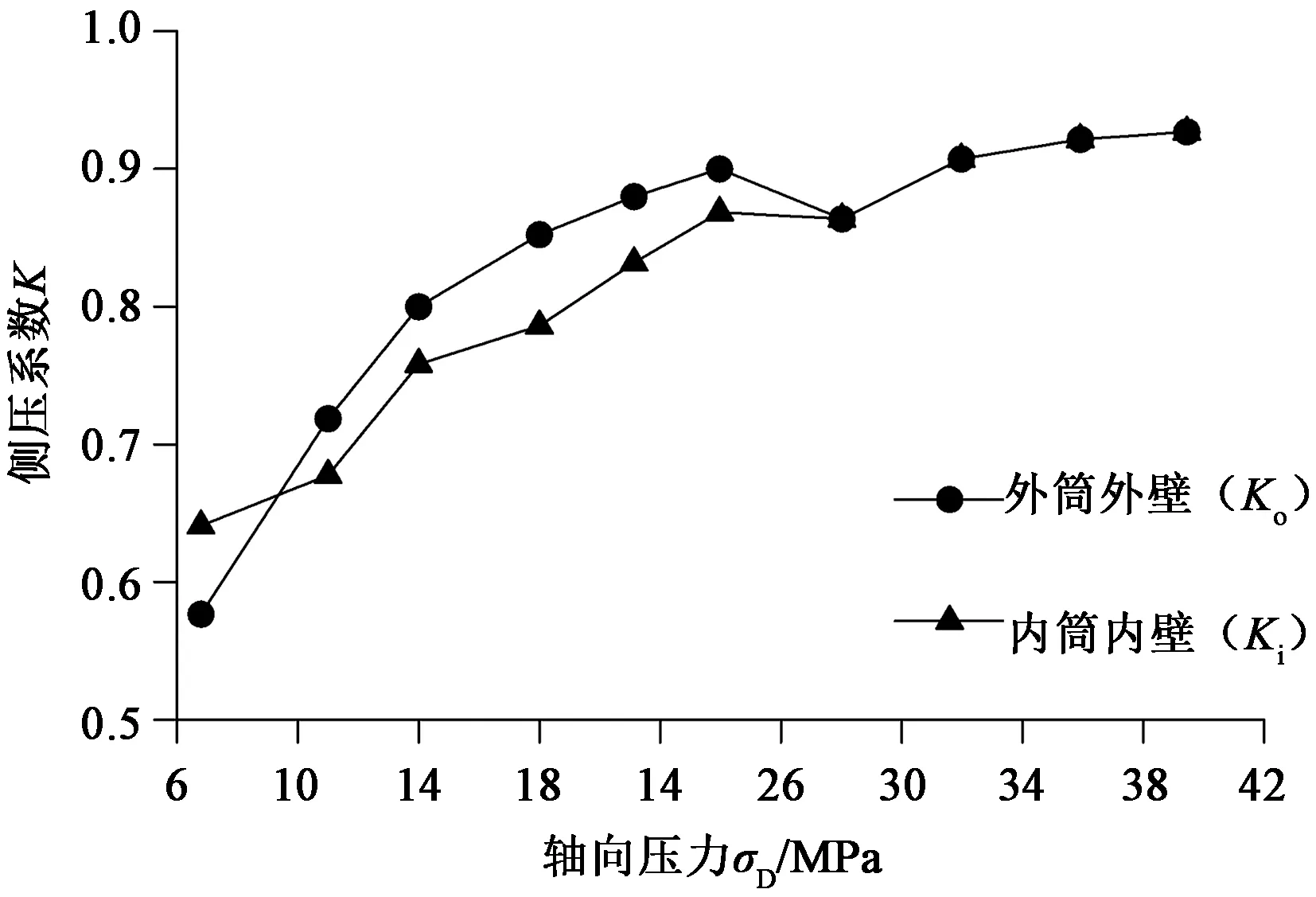
图4 文献[4]侧压系数数据Figure 4 Side pressure coefficient data of the document [4]

从图4中可以看出，K1、K2总体接近，随轴向压力增加而增加，到25 MPa左右时与加载轴向力关系不再明显，K1、K2总体介于0.6～0.9之间。但不同的试验有不同的结果，一般情况下K1、K2在0.5～1.0之间变化。本次计算简化处理，采用侧压系数为K1为0.8，K2则采用公式(6)进行计算(也可以认为两者相等，计算更简化)。

3 摩擦力计算

填料和阀杆的摩擦力是一个很重要的问题。一方面摩擦力会对填料本身造成磨损，影响密封性，另一方面可能影响阀门的开关以及阀门的调节灵敏度，甚至出现阀杆卡涩、抱死现象。文献[5]中通过试验测定了不同轴向压力不同多次往复情况下的摩擦力，见图5，其填料尺寸外径为∅45.6 mm，内径∅30 mm，高度10 mm，填料总高度为50 mm，此次项目填料尺寸分别为56 mm、40 mm和6 mm，尺寸接近，具有参考意义。

图5 文献[5]摩擦力数据Figure 5 Friction data of the document [5]

从图5中可以看出，随着往复次数的增加，摩擦力逐渐增大，说明磨损量会增加摩擦系数，增加摩擦力。在30 MPa的轴向力下，摩擦力就有5000 N左右，文献[9]提到摩擦力矩可以占到阀门开启关闭力矩的14%～26%。因此，有必要通过详细结构设计和其他工艺加工措施降低阀杆摩擦力。

其计算公式为：

(7)

4 结构设计

经初始计算发现，填料高度H不宜过大，否则摩擦力太大。根据经验，以3～5圈为宜，过多则摩擦力过大，且对密封意义不大，过小则密封长度有限。其结构采用图1所示常用结构，即设置压盖和两个螺栓。实际过程中，轴向应力是通过施加螺栓预紧力实现的，通过相关计算公式[8]，得到相应的轴向应力。初始设计分别设计4、5、6圈填料下不同螺栓预紧力的计算情况，见表1、表2和表3。

表1 4圈填料(H=24mm)计算表Table 1 Calculation of four circles stuffing (H=24 mm)

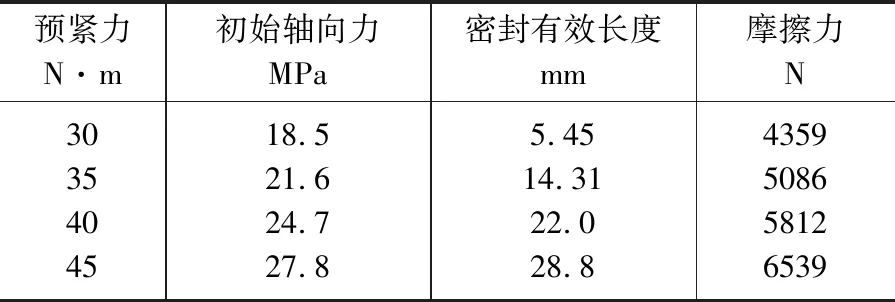
表2 5圈填料(H=30mm)计算表Table 2 Calculation of five circles stuffing (H=30 mm)

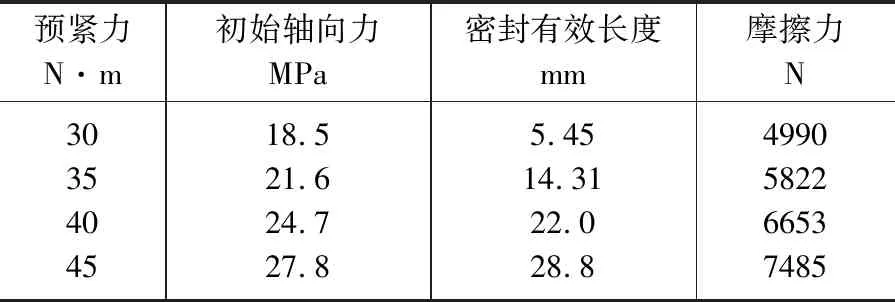
表3 6圈填料(H=36mm)计算表Table 3 Calculation of six circles stuffing (H=36 mm)

从以上计算结果可以看出，密封长度由轴向应力决定，可参见计算分析。其中表1预紧力45 N·m时密封长度为24 mm，与表2、表3不同，这是因为表1仅仅只有4圈填料、24mm的长度，但表2、表3计算的密封长度则相同。此种情况，密封长度大于填料总高度，表示此种情况没有无效密封区。

以图表的形式表示出不同填料圈数预紧力(轴向应力)摩擦力的对应关系，见图6。

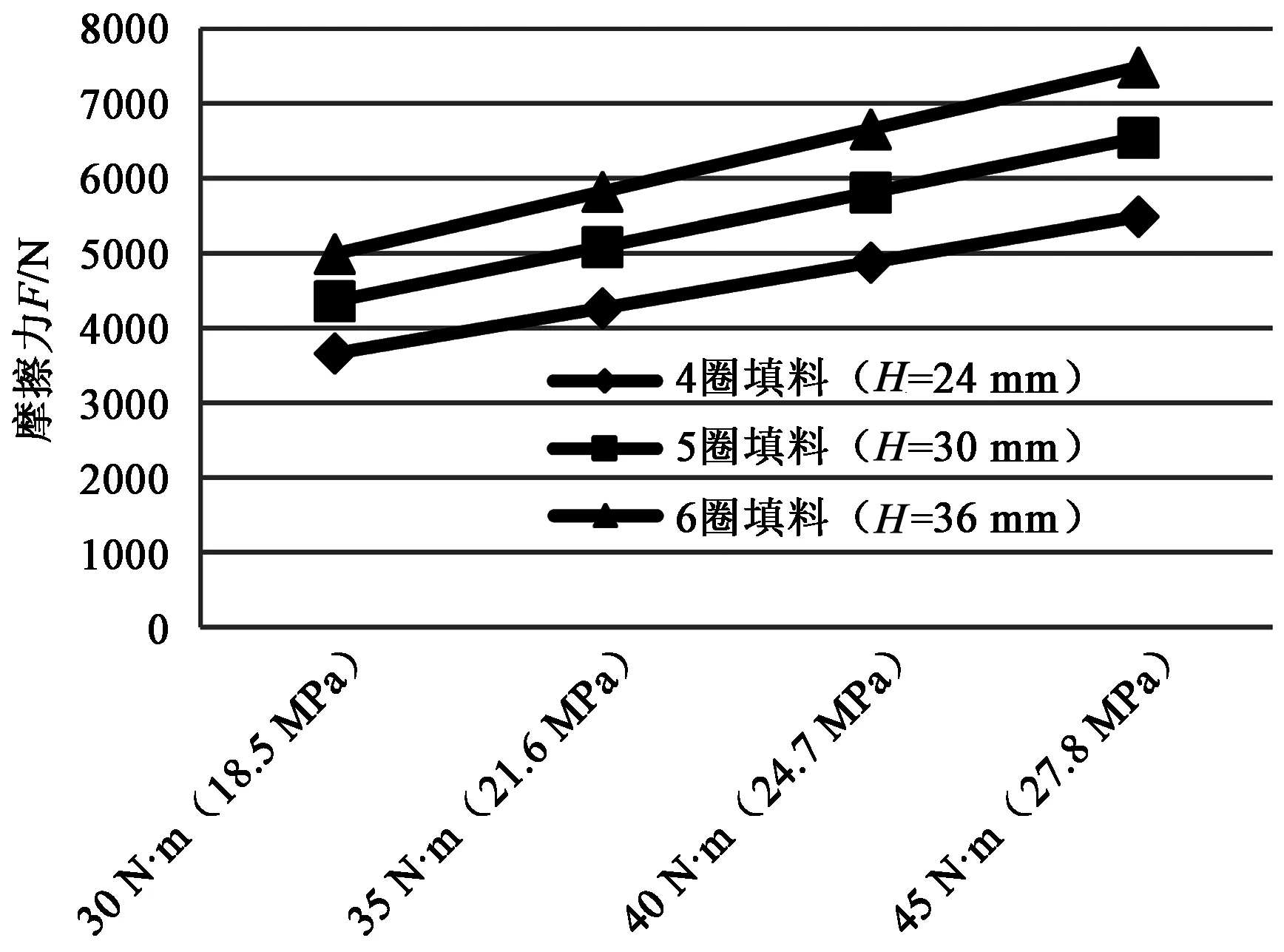
图6 计算预紧力-摩擦力数据Figure 6 Calculated data of pretightening force-friction

由图6可知，同样的预紧力下圈数越多摩擦力越大，同样的圈数下预紧力越大摩擦力越大。同时很容易发现，摩擦力与预紧力明显呈线性关系。但截取图5中试验数据发现，二者关系并非线性，而是偏指数变化，见图7。造成此种差别的主要原因应是侧压系数，由图4试验数据发现，侧压系数随轴向力增加而增加，而计算中假定侧压系数为常数。

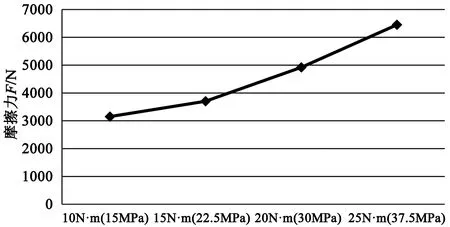
图7 图5试验数据Figure 7 Testing data of theFigure 5

目前常用的填料结构并非单一的柔性石墨填料，而是组合填料。组合填料由两种填料组成，前后两端为金属丝编织加强的石墨填料环，中间部分为高纯度的柔性石墨环。前后两端填料环偏向于支持中间的石墨环，并防止流体中细微颗粒进入密封间隙或阻止石墨挤压进入密封腔内；而中间部分则偏向于密封作用。因此4圈填料实际起到密封作用的只有2圈，总长度12 mm，相对偏少；从摩擦力角度看，6圈填料显然高于5圈填料，但对于密封性无提升。因此，选择5圈填料。考虑到金属丝编织填料的作用，选择密封长度为22 mm和28.8 mm的情况，此时摩擦力分别为5812 N和6539 N，螺栓给定预紧力为40 N·m和45 N·m。

实际运行过程中由于阀门振动、螺栓松弛等因素，螺栓的拉力会不断降低，影响密封性，甚至造成泄漏。文献[6]提到了活载荷结构，即在螺母下安装碟簧，保持螺栓预紧力的稳定性。采用这种改进措施解决了高参数阀门的泄漏问题。

基于以上分析计算，填料密封设计结构如图8所示，设置2个M16的压紧螺栓，给定预紧力40 N·m ～45 N·m，并设置碟簧保持螺栓预紧力。填料为组合填料：2圈金属丝编织石墨填料+3圈高纯柔性石墨填料。

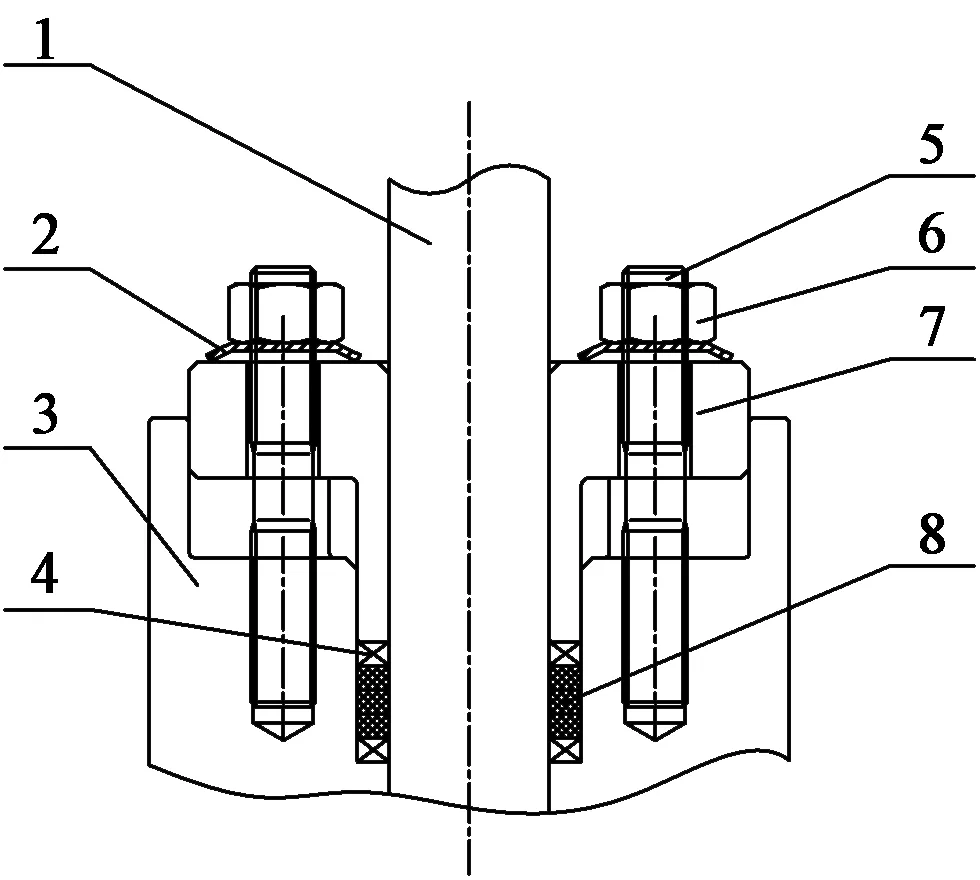
1—阀杆 2—碟簧 3—填料函(阀盖) 4—金属丝编织石墨填料 5—压紧螺栓 6—压紧螺母 7—填料压盖 8—高纯柔性石墨填料图8 填料密封设计结构Figure 8 Design structure of stuffing seal

5 结论

介绍了填料密封的结构原理和理论计算，重点分析了填料压力分布，也指出了设计中应当注意的问题。如设计计算中应关注摩擦力、填料总高度；结构设计中应设置碟簧等类似的结构，以保持螺栓预紧力；填料密封采用组合填料密封，更好地发挥作用。这些都为以后设计填料密封提供了有益的参考。