基于案例分析的初中数学几何基本图形的教学探索
2019-10-25江苏省苏州工业园区唯亭学校顾成华
江苏省苏州工业园区唯亭学校 顾成华
在进行几何教学过程中,常会发现有些学生面对一些陌生的问题时往往束手无策,也有不少学生只会做那些刚见过、做过的,比较熟悉或相似的题目。当学生不会做题时,问他在思考时都想到了什么,他往往会回答:“大脑中一片空白,不知道怎样想。”学生提炼不出解题思路的根本原因,笔者以为是学生不能把问题化归转化,是缺乏分析推理能力的表现,究其原因,是对数学基本图形不熟悉。教师需要在平时的教学过程中有意识地帮助学生提炼基本图形,强化训练基本图形。教师应告诉学生:在分析几何问题时,首先要试图找出、分离适当的基本图形,如果不能找到完整的基本图形,那么要根据题干中的线索去捕捉部分基本图形,这时可通过添加适当的辅助线来构造完整的基本图形,进而应用基本图形的性质来解决具体的问题。显然,学生习得、提取基本图形的能力还有待提高。
一、基本图形的概念
所谓基本图形,应该是我们分析解决几何问题时,从问题图形中分离出来的最简单、最基本、最重要而且具有特定性质的图形。从基本图形运用的难易程度来看,它可以分为两类:第一类是现行初中数学教材中出现的定义、公理、定理以及推论所对应的图形,第二类是在教材对应的例题、习题、练习中发现的具有典型性的图形。第一类基本图形是第二类基本图形的基础,第二类基本图形通常是由几个第一类基本图形组合而成的。
图1 是定理“三角形中位线平行于第三条边,并且等于第三边的一半”所对应的基本图形,属于第1 类基本图形,图2 是“中点四边形”所对应的基本图形,由对角线相等可得中点四边形是菱形,由对角线互相垂直可得中点四边形是矩形,反推亦成立,这就属于第2 类基本图形。
二、初中数学几何教学中对于基本图形教学的几点思考
《数学课程标准》在几何方面的学习要求是让学生“能从较复杂的图形中分解出基本的图形,并能分析其中的基本元素及其关系,利用直观来进行思考”。基于多年的教学实践及平日的探索,笔者以为,应把习得基本图形、直接提取基本图形、间接提取基本图形相结合,从而实现对基本图形的掌握和灵活运用,这可通过以下几个步骤实现:
1.通过教学习得基本图形,熟知基本图形的条件和结论以及证明或求解的方法
教材中几何的复习课一般都是几何的定义、定理、推论等的进一步学习,往往可以对已经习得的知识进行更高层次的升华,而它们所对应的基本图形就是前面所说的第2 类基本图形,因此教师在上课时要注重对这些基本图形的总结和提炼。
苏科版八年级上册第3 章第3 节“勾股定理的简单应用”有这样一道题:一根竹子原高一丈(1 丈=10 尺),中部有一处折断,竹梢触地面处离竹根3 尺,试问折断处离地面多高?
这道实际问题转化为数学问题就是:如图3,已 知∠C=90 度,AB=BD,AC=10,CD=3,求BC的长度。
在这道题目中,已知直角三角形三边中一边CD的长度以及另外两边BC、BD的和,因此可以设BC为x,则BD为10-x,利用勾股定理得到方程进行求解,本题中还可以求出AB和BD的长度。
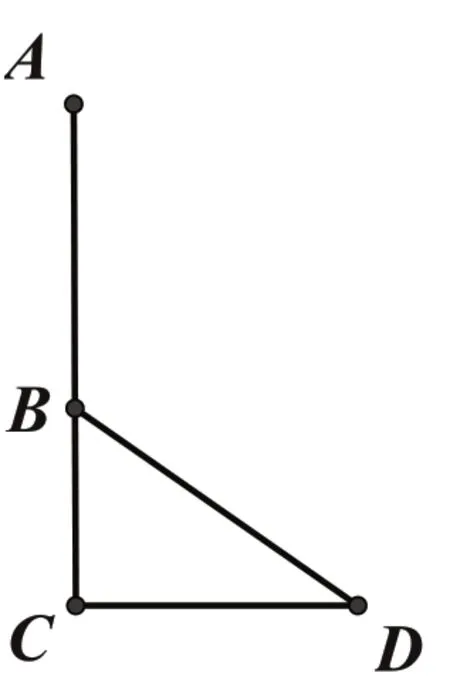
本题还可以改编成:在Rt △BCD中,∠C=90 度,AB=BD,已知AB、BC、AC、CD中任意两条线段的长度,你能求出其他线段的长度吗?
答案是都可以求出来的,因此,可以得到这个基本图形的条件是:直角三角形,两条线段相等,知道两条线段的长度(不包括题中两条相等线段的情况),可以求出基本图形中其他线段的长度。
这是勾股定理和翻折构成的基本图形,属于第2 类基本图形,由于此图形形状类似于红旗,为了方便学生记忆,遂把这个基本图形定名为“红旗模型”。
红旗模型还有一些其他结构,比如《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐。问水深、葭长各几何?”题意是:有一个池塘,其底面是边长为10 尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1 尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图4)水深和芦苇长各多少尺?

本题转化为数学问题是:如图5,已知∠CBD=90°,AC=CD,AB=0.5,BD=2,求BC的长度。

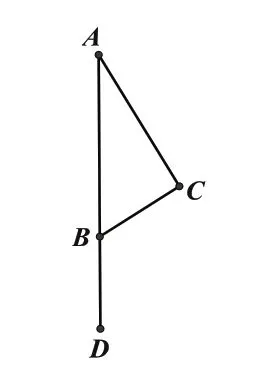
再比如:如图6,∠ACB=90°,BC=BD,已知AD和AC的长度,可以求BD,BC,AB的长度。这两道题都可以进行类似的改编,解题方法也都和图3 类似。
2.通过发展条件和结论反推,直接提取基本图形解决问题。
所谓直接提取基本图形,就是在有其他图形干扰的情况下,能够根据条件或结论找出基本图形。因为通过学习已经对某个基本图形有所了解和理解,学生就能有的放矢,直接依据题设条件或结论提取相应的基本图形,并运用基本图形的性质解决问题,例如:
如图7,折叠直角三角形ABC,使直角边AC落在斜边AB上(AD为折痕,C落在E上),已知AC=6,BC=8,求CD的长。
解答:由勾股定理易得AB=10,BE=4,由翻折得CD=DE,故可以找到如图8 的基本图形,即可求出答案。
变式:如图9,折叠直角三角形ABC,使点B落在点A上(DE为折痕),已知AC=6,BC=8,求CD的长。
解答:可在图形中直接找到基本图形,如图10,大多数学生都可以又快又准确地完成这道题。
3.通过添加适当辅助线,间接提取基本图形解决问题
如果无法直接提取基本图形,可考虑作适当的辅助线来构造基本图形,通过间接提取基本图形来解决问题。在学生极其熟悉基本图形,能够准确提取后,就要引导学生能辨认出略带残缺的基本图形,经过多样的反复训练后,使其内化成为学生的数学素养,并能在应用过程中举一反三。
笔者挑选了几个典型的题目,结合自己的教学心得,谈谈这个解题技巧,以作参考。
例1:如图11,矩形OABC在平面直角坐标系xOy的第一象限内,点C在x轴正半轴上,点A在y轴正半轴上,连接AC,将矩形OABC沿AC翻折,使点B落在点D的位置,若点B的坐标为(2,1),则点D的坐标是_________。
解答:设CO与AD相交于点E,折叠后CD=CB=OA=1,由平行线、角平分线构成的基本图形可得等腰三角形ACE,再设CE=AE=x,在Rt △AOE中,由勾股定理求出x的值,然后作DF⊥x轴,根据△AOE∽△DFE即可得出答案。
评注:本题是利用相似三角形对应线段成比例建立方程求解,困难之处在于比例式中有部分线段长度未知,通过翻折构造红旗模型,如图12,则可化解这一难点。
例2:如图13,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5。在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK。如何折叠能够使△MNK的面积最大?请你探究可能出现的情况,求出最大值。
解答:(1)将矩形纸片对折,使点B与点D重合,如图14。此时点K也与点D重合,由平行线、角平分线构成的基本图形可得等腰三角形DMN,再设KM=x,则AM=5-x,由勾股定理求出KM和KN的值,最后求出△MNK的最大面积。(2)也可将矩形纸片沿对角线AC对折,如图15,下面的解法和第(1)种情况相类似。
评注:问题中,两种翻折情况均是先画出翻折后的图形,通过构造基本图形——红旗模型求出KN的长,再借助求KN的最大值求出△MNK面积的最大值。
笔者仅以勾股定理与翻折的基本图形“红旗模型”这一基本图形为例,探索了如何教会学生习得基本图形、直接提取基本图形、间接提取基本图形,最终解决问题的教学思路,也试图以此抛砖引玉,与其他同仁探讨基本图形的教学策略,完善基本图形分析法,让我们的课堂教学更高效,让学生的解题能力更高强,以达到双赢的结果。
