古典概型教学方式研究
2019-10-25上海电机学院文理学院刘美玲
上海电机学院文理学院 刘美玲
古典概型也叫传统概率或等可能概型,其定义是由法国数学家拉普拉斯 (Laplace)提出的。内容简单,但数学题目千变万化,在多年的教学实践中发现,学生在古典概型的概率求解中依然存在很多问题。
一、古典概型定义
(1)试验的样本空间只包含有限个样本点;
(2)试验中每个基本事件发生的可能性相同。
具有以上两个特点的试验称为古典概型或等可能概型。
二、古典概型计算公式
设试验E的样本空间由n个样本点(基本事件)构成,A为E的任意一个事件,且包含k个样本点(基本事件),则事件A出现的概率记为:

这里解释基本事件的发生概率相同,所以一个事件的概率值即是事件所含基本事件的个数除以基本事件总数。常见的古典概型有掷硬币试验、掷骰子试验、摸球试验等。具体的计算举例说明,以下两个例题分别取自参考教材[2][3]。
例1:设袋中有10只球,编号分别为1,2,…,10. 从中任取3 只球,求:
(1)取出的球最大号码为5 的概率;
(2)取出的球最小号码为5 的概率;
(3)取出的球最大号码小于5 的概率。
解:设A={取出的球最大号码为5},B={取出的球最小号码为5},C={取出的球最大号码小于5},基本事件总数为。
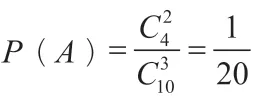

(3)由于取出的三只球中,最大号码小于5,C所包含基本事件的个数为,
本题目中取球的方式是任意的,每个球被取到的概率都是一样的,所以是古典概型。另外,只要观察取出来的号码,没有顺序问题,所以用组合数计算。下面再看另一个例题:
例2:一个家庭中有两个小孩,已知其中一个是女孩,问另一个也是女孩的概率是多少?(假定生男生女是等可能的)
解法1:由题意知,样本空间为:
Ω={(男,男),(男,女),(女,男),(女,女)}
A表示事件“至少有一个是女孩”,B表示事件“两个都是女孩”,则有:
A={(男,男),(女,男),(女,女)},B={(女,女)},
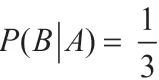
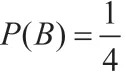
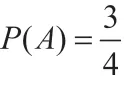
本题目解法1 用古典概率公式计算,较为烦琐。实际上,这是典型的条件概率问题,用条件概率公式则可以简洁地计算出结果。条件概率在后续的学习中经常用到,例2 是一个曾经在网络盛传过的小题目,这里经过条件概率的理论解释和计算,想必大家都能了解什么是条件概率了。条件概率的计算和应用是非常多的,全概率、贝叶斯以及随机变量的计算中都会用到,所以从这个例题引出其重要性和基础性,激发学生认真学习、理解透彻。
