数形结合思想在小学数学教学中的应用

江苏省兴化市特殊教育学校 顾晓琴

数形结合，从概念上来讲是指把复杂和抽象的数量关系和思维过程转化为比较直观的图形进行分析和构建解题联系，使得数学题目的难度和思维深度得到一定程度的降低。在小学数学教学过程中，灵活恰当利用数学结合思想，不仅可以提升小学数学教学的高效性，还可以促进小学生数学核心能力的提升。小学生作为独特的教学群体有着自己的学习特点，对于直观的图形有着莫名的学习兴趣，数形结合思想理论下的教学方法符合小学生的思维发展需求，切合小学生的数学认知程度，有利于全面激发小学生的数学学习兴趣和课堂学习的主动性，落实了小学数学教学核心素养的基本要求。因此，在小学数学教学过程中，结合具体的教学内容教师要合理引入数学结合思想，提升小学生的数学综合素质。

一、结合教学难点，利用图形引导学生探究

数形结合思想体现在小学数学教学的整个阶段，通过数学转换方法可以把抽象的数学概念和知识转化为形象的图像，有利于降低教学难度增强小学生主动学习的能力。在小学数学具体教学环节中，利用数形结合思想可以降低数学难度，突出数形结合的直观性和生动性，有利于小学生数学观察能力和思维能力的发展，逐步增强了小学生对数学学科的个人认知能力。因此，数学结合思想通过把抽象的数、概念和脑子理解的内容有利于突出数学难点，结合数学教学的重点内容展开教学，有利于小学生掌握复杂的数学内容提升自己的数学探究能力。

例如，在小学数学教学过程中，教师可以通过几何图形的直观性来突出教学难点，使得抽象的数学问题变得具体直观化。如有数学题目：有辆汽车从甲地开往乙地，先上坡速度为20km/h，后下坡速度为40 km/h,用时2h 平均速度为30km/h。从乙地开往甲地需要花费多少时间？这道题目的求解需要构建一个等量关系，教师可以通过画出直观的几何图形辅助小学生进行理解，通过图形，小学生理解了解题的难点，图形使用不仅激发了小学生的数学学习兴趣，而且有利于突出解题难点提高小学生的数学解题效率。

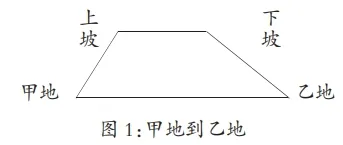
图1：甲地到乙地

二、结合思维要求，利用图形激发学生思考

在数学学习过程中，数学思维能力的重要性是小学生提升数学素养的有效途径。小学数学教学有着自己独特的特点，通过初步高中数学概念，结合小学生的个人兴趣和认知规律进行思维教学，教师在具体的教学过程中可以紧紧围绕数形结合内容进行小学生数学核心素养的培养。有效利用数形结合思想，不仅可以充分发挥小学生的数学创造力和思维想象力，还可以使得复杂的数学问题变得具有一般的思维性和规律性，使得奠定小学生良好的数学基础，又可以有效培养小学生的数学思维能力。

例如，在小学数学“正方形和长方形的初步认识”的教学过程中，教师可以利用数形结合思想进行课堂教学，从而有效提升小学数学课堂教学质量。像在进行礼品包装时，想要把长20cm,宽15cm 和高5cm 的两盒糖果包装成一包，试问怎样包装可以尽量节约纸张。在具体的教学实际操作环节，教师可以提供准备材料供小学生进行亲自动手实践，在小学生有初步的实践基础能力上，教师可以总结一个表格归纳三种不同的方法，提升教学效果和小学生的数学核心素养。

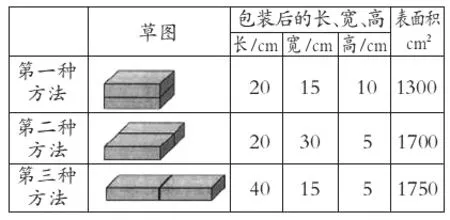
三、结合解题重点，利用图形培养学生能力

在新课程教学背景下，小学数学改革逐步推进教学内容从知识概念教学已经延伸到能力和素质教学。数学的本质就是利用一种开阔的数学思维来看待问题，从而揭示数学现象和背后的数学规律，通过有效的数学归纳和总结形成数学思想和核心素养。因此，在小学数学教学过程中，教师应该从基本的数学解题能力培养进行教学，通过有效的能力培养和教学习惯渗透使得小学生逐步增强自己利用数学解题能力和应用知识的能力。数形结合思想的利用，使得小学生在培养数学能力过程中可以全面和深入地考虑问题，小学生也可以更加深刻地理解数学问题和数学思维，使得小学生的数学基本技能获得根本性上的发展。

例如，在实际教学过程中利用数形结合思想进行教学，可以帮助小学生更好地理解数学教学内容，应用数学教学方法提升数学解题能力。像在某一个具体题目教学中：一个钟表只有时针运行正常，分针每小时走80 分钟，并且是倒着走，那么假设该钟表在六点半时显示时间正确，下次显示时间正确是什么时候？利用数形结合思想进行解题不仅使得小学生对数学题目认识更加深刻，还可以提升小学生的数学解题能力。

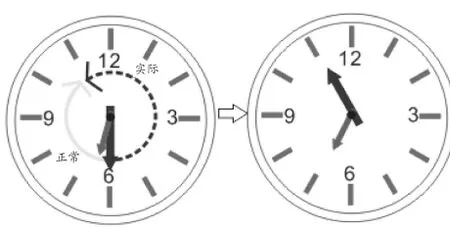
总而言之，将数形结合思想运用于小学数学教学过程中，不但可以激发小学生的数学学习兴趣，还可以帮助小学生更直观地理解数学概念，提升小学生的数学解题能力。数形结合思想是小学数学教学过程中最重要的思想，有利于全面提升小学生的数学核心素养和综合能力。