中考数学压轴题中的“动点”问题的分析及对策

广东省佛山市南海区桂城街道文翰中学 李艳汕

数学学科中的“动点问题”主要是指在数学题的题设图形里有一个或者多个“动点”且该动点在其线段、弧线或者射线等上面的位置是运动变化的一类开放性的数学题目，也就是从变化和动态的角度来探究三角形、四边形与函数图像等之间的变换关系。通过对图形中的图形、对称性以及动点变化规律的研究来探究各种图形的性质与特征。在解决这类数学题目的过程中通常需要空间思维能力与逻辑推理能力的发挥与运用。

【例1】如图1 所示，抛物线经过A（-3，0)，B(0，4)，C(4，0）三点。

（1）求抛物线的解析式。

（2）已知AD=AB（且D在已知线段AC上），存在动点P从点A沿线段AC以每秒1 个单位长度的速度移动；同时另一个动点Q以某一速度从点B沿线段BC移动，经过t（s）的移动，线段PQ被BD垂直平分，求t的值。

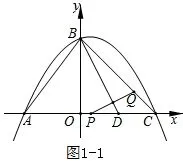
图1

（3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ+MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由。

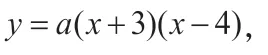
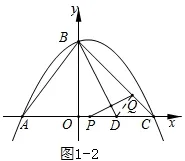
图2

（2）已知AD=AB可求出点D的坐标，由于AP=t,所以PD的长度可表示出来；由AD=AB可知∠ABD=∠ADB，因为PQ被BD垂直平分，所以PD=QD，可以得到∠PDB=∠QDB，如图2 所示。

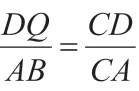
（3）因为点A，C是抛物线与x轴的两个交点，所以点A和点C关于抛物线的对称轴直线对称，因此MA=MC，于是当A,M,Q三点共线，即点M为AQ与直线的交点时，MQ+MC的值最小。

（1）求该抛物线的解析式。

（2）点Q是线段AB上的动点，过点Q作QE∥AC,交BC于点E，连接CQ。当△CQE的面积最大时求点Q的坐标。

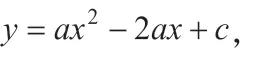
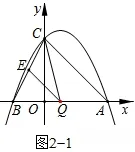
图3

（2）发现△CQE的面积受点Q的位置的变化而变化，当点Q的位置变化时，△CQE的各条边的长度和各个角的大小都在变化，因此利用恰当的方式表示△CQE的面积是解决问题的关键。

如图4，因为QE∥AC，所以可以利用AQ表示CE的长度，将CE作为△CQE的底边；而∠B的大小不变，因此可以利用BQ的长度和∠B的三角函数值来表示△CQE的底边CE上的高。

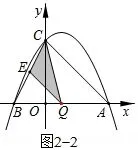
图4

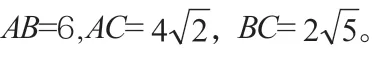
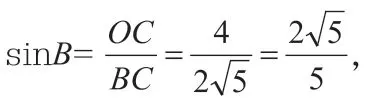
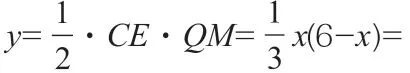
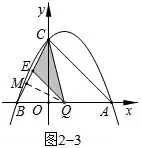
图5

所以当x=3 时，即AQ=3,此时点Q的坐标为（1，0）时，△CQE的面积有最大值3。

求三角形或四边形的面积最大值问题过程中通常要利用函数知识，在表示图形的面积时，有时需要对图形进行割补，割补的原则是能利用动点和一些定点的坐标表示图形的底边长和对应的高，然后利用面积公式建立变量之间的函数关系，再利用函数的知识求解最值问题。

课改后数学卷中的数学压轴题正逐步转向数形结合、动态结合、实验探究等方面发展，这些压轴题题型繁多、题意创新，其主要目的是对学生自主探究能力、分析推理能力、解决问题的能力、空间的想象能力以及对所学知识的实践运用能力等的考查。通过对历年来各个地区考试压轴题的分析与总结，可以发现今后中考数学试题的考查热点以及命题发展方向。因此，只有深入探究中考试题，把握中考发展方向，才会更有针对性地培养学生的数学学科核心素养，促进学生朝着更加科学、正确的方向发展。