Markov-Hurwitz 型方程研究

上海市世界外国语中学 熊浩明

定义1：我们称x2+y2+z2=kxyz为Markov 方程（其中k是正整数），有以下结论：

定理1：如果Markov 方程有正整数解，那么k≤3。

具体地，当k=1，3 时，有正整数解；而当k=2 时，没有正整数解。

事实上，我们有更一般的结果：

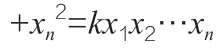
一、主要结果

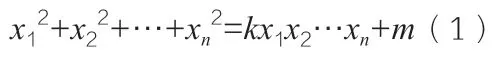
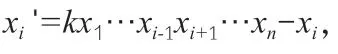
定义4：如果通过韦达变换使得方程（1）的正整数解(x1，x2，…，xi，…，xn）→(x1，x2，…，xi'，…，xn），对1 ≤i≤n，其中xi'=kx1…xi-1xi+1…xn-xi＞0，则称(x1，x2，…，xi，…，xn）与(x1，x2，…，xi'，…，xn）是等价的。

对Markov-Hurwitz 方程所有等价的解记为某个等价类，即相同等价类中的两个解可以通过一系列的韦达变换得到，而不同等价类中的解是无法通过韦达变换得到的。如果一个正整数解通过韦达变换无法得到另一个正整数解，则它本身构成一个等价类。在每个等价类中，我们记最小的那个解为极小解（即各变量的和为最小，但未必唯一）。如果有s个等价类，那么就有s个极小解。极小解也称为基本解，各个不同的基本解是无法通过韦达变换转化的。

如果令0 ＜x1≤x2≤…≤xn，当k≥2 时，由韦达变换的定义，我们发现一般的韦达变换会将解的各变量的和增大，除非i=n，即变换xn'=kx1x2…xn-1-xn，它是唯一可能使解减小的变换。我们得到如下的重要结果：

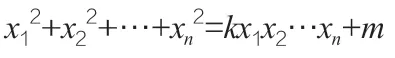
二、定理的证明

首先我们给出定理2 的证明。

定理2：对n≥3，k为给定正整数，如果不定方程x12+x22+…+=kx1x2…xn有正整数解，那么k≤n。

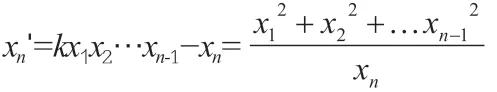
如果xn=1，那么x1=x2=…=xn=1，这就得到k=n。

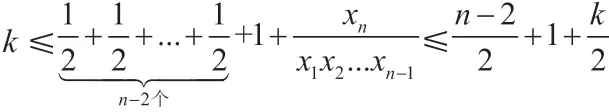
即得k≤n。

所以我们证明了定理2。

定理3 是本文的核心定理。接着给出定理3 的证明：

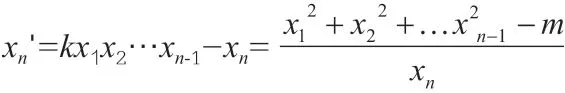
所谓“医养结合”就是指将医疗资源与养老资源结合起来，实现资源效率的最大化，使养老机构既具有养老功能又具有医疗功能，是一种把生活照料与医疗服务融为一体的新型养老模式。然而，广西在“医养结合”工作方面进展缓慢，地方政府及相关部门没有按照“医养结合”的本质要求来研究和制订实施方案，因此，包括营利性养老服务机构在内的广西各类养老服务机构的“医养结合”工作没有太大起色。

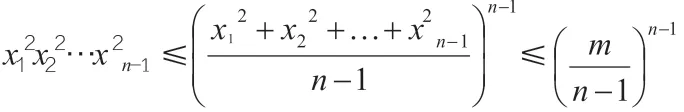
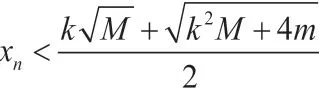
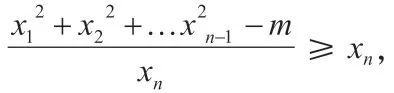
这就证明了基本解的个数是有限个，即存在一个基本解的有限集合{A1，A2，…，As}，方程的所有解都可以由这个集合中的元素生成。

我们现在对k=1,2 的情况作些说明，这时的方程有可能出现无限多组基本解：

（1）如果k=2，更细致地分析上述不等式（＊）：

当xn-2=1 时，此时方程成为x2+y2+n-2=2xy+m，即（x-y）2=m+2-n，令m+2-n=s2，则xn=a+s,xn-1=a是最小解，如果s＞0，由于韦达变换将（a，a+s）→（a+2s，a+s），所以基本解为（1，…，1，1+s）,（1，…，1，2，2+s，），…，（1，…，1，s，2s）这s组；如果s=0，那么(x，y)=(a，a)无法通过韦达变换互相得到，此时原方程有无穷多组基本解：(1，…，1，a,a)。

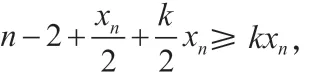
当xn-2=2，且x1=x2=…=xn-3=1 时，原方程变为：x2+y2+n+1=2xy+m，即（x-y）2=m-n-1，当m=n+1 时，x=y=a，此方程的基本解为(1，…，1，2，a,a)，为无限多组，当m-n-1=s2＞0 时，此方程的基本解为(1，…，1，2，a,a+s)，a=1,2,…，s，共s组。

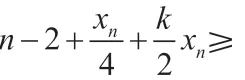
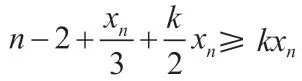
上述分析指出，只有在k=2，m=n-2 时或者k=1，m=n+1 时，方程存在一组无限的基本解，其余情况方程的基本解都是有限组，我们可以得到如下的结果：

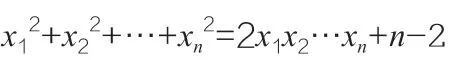
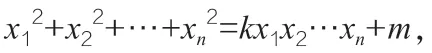
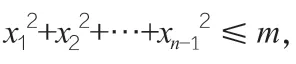
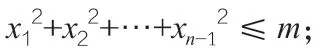
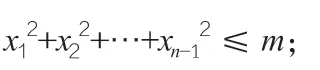
注：当m＞0 时，上述xn的不等式是严格的，即等号不成立。

实践证明，当n不太大时，这种方法是有效的，而在m不是很大时，我们甚至还能证明某些方程无解。但对k=1 的情况较复杂。

对n=3，我们研究一些特殊的Markov-Hurwitz 方程的解的结构。

【命题2】Markov-Hurwitz 方程x2+y2+z2=xyz+1 无正整数解。

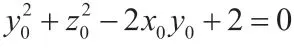
【命题3】Markov-Hurwitz 方程x2+y2+z2=65(xyz+1)的基本解是(1,8,520)与(4,7,1820)。

四、总结

本文围绕Markov-Hurwitz 方程展开研究，在这个过程中提出了一些颇有意义的定理和推论，并给出了自己的证明。