基于增量学习的高光谱图像目标检测

张 宁，陈嘉杰，伍 伟，沈 霁，袁 杰，朱新忠，谢凤英

(1.上海航天电子技术研究所，上海 201109； 2. 北京航空航天大学 宇航学院，北京 100191)

0 引言

高光谱图像在获得物体空间信息的同时，也包含了丰富的光谱信息，其每个位置的像素都包含一条近似连续的光谱曲线[1]。相比于普通遥感图像，高光谱图像的空间分辨率较低，但光谱分辨率很高，因此可以利用物体的光谱特性进行区分。高光谱图像的目标检测可以应用于很多领域，包括军事侦查、资源探测、植被分析等[2]。

高光谱图像目标检测按照目标光谱是否可知可分为目标检测和异常检测。基于先验光谱信息的目标检测本质上可视为一个二元分类器(目标-背景)。常见的高光谱目标检测算法包括光谱角度匹配法[3-4](spectral angle mapping, SAM)、自适应一致估计法[5-6](adaptive coherence estimator, ACE)、正交子空间投影法[7](orthogonal subspace projection, OSP)、约束能量最小化算法[8-10](CEM)稀疏表达法[11-12]和基于变分的检测方法等[13]。其中CEM利用特定的约束条件设计一个有限脉冲响应滤波器(FIR)，增强目标光谱，抑制背景光谱。与其他目标检测方法相比，CEM只需要知道目标的光谱先验而不需要背景光谱先验，应用范围更加广泛，且在消除未知信号及抑制噪声方面有显著优势[14]。然而真实环境中捕获的高光谱数据通常会受到环境因素的影响(如大气散射、湍流、光照条件、成像噪声等)，与已知的光谱先验不完全一致[15-16]，此时只用光谱库中的光谱作为先验很难得到较好的检测效果。

针对光谱先验与实际环境中的目标光谱不一致的情况，本文在CEM检测的基础上提取相应的目标与背景光谱，并通过增量学习的形式更新检测器。该算法不需要重新计算所有样本的自相关矩阵，能够以很小的计算资源提高检测精度，在星上在轨目标检测领域有重要的应用价值。

1 约束能量最小化检测算法原理

CEM的目标是从能量的角度压制背景从而提取目标。为此，HARSANYI设计了一个有限脉冲响应滤波器[8]，通过添加目标光谱先验的输出为定值的约束，CEM能抑制背景信息而使目标像素保持较大的输出，从而有效地分离目标光谱与背景光谱。

设高光谱图像中所有像元构成的样本集为X={x1,x2,…,xN}，其中xi=(xi1,xi2,…,xiL)T为第i个样本，N为像元的数目，L为每一像元的波段数，d=(d1,d2,…,dL)T是已知的目标光谱先验，CEM的目的就是设计一个有限脉冲响应滤波器w=(w1,w2,…,wL)T，使经过该滤波器后，目标光谱仍能保持一定大小的输出，而背景光谱得到抑制，因此滤波器应该满足如下约束：

(1)

对于高光谱图像，其经过滤波器后的平均输出“能量”可用每个像素的输出值的平方和来表示，具体可写为

E{y2}=E{(wTx)2}=wTRw

(2)

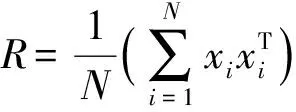
(3)

对于式(3)所示的条件极值问题，可以运用拉格朗日乘子法对上述问题进行求解，得

(4)

式中：wCEM代表了最佳的滤波器系数。这个系数在保持已知目标输出不变的情况下有效地抑制了背景，使重要的目标信号能够被提取。对于任意输入向量xi，CEM滤波器的输出响应yi为

(5)

2 基于增量学习的约束能量最小化检测

约束能量最小化算法的核心思想是使背景光谱的平均输出能量最小，通过优化，目标与背景的输出得到了一定程度的区分。然而，单层的CEM检测器的检测精度是有限的。

针对上述现象，本文从增量学习的角度出发，将多层CEM进行级联，保留每一层迭代中对滤波器响应较大的光谱向量，同时抑制响应较小的光谱向量，以增加光谱和背景的区分度，并利用Sherman-Morrison定理，省略了后续级联层中自相关矩阵的计算，在简化计算复杂度的同时提升了CEM的检测精度。其理论推导如下：

设Rk和Rk-1为相邻两次迭代的自相关矩阵，则有

Rk-Rk-1=

(6)

其中,

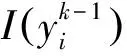
dm=xi,ifyi=max(y)

(7)

(8)

式中:α为满足条件的光谱个数。

用背景光谱的平均值近似表示被抑制至0的背景光谱，同时忽略那些未被抑制或抑制不明显的光谱，则式(6)可以简化为

(9)

Sherman和Morrison等提出了通过矩阵分解求解逆矩阵的一种方法[17]。基于Sherman-Morrison定理，下一次迭代的自相关矩阵的逆矩阵可以表示为

(10)

而新的目标光谱dk可表示为

(11)

式中:k为迭代次数。

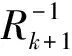
E{(yk)2}-E{(yk-1)2}<ε

(12)

基于增量学习的约束能量最小化算法流程如图1所示。

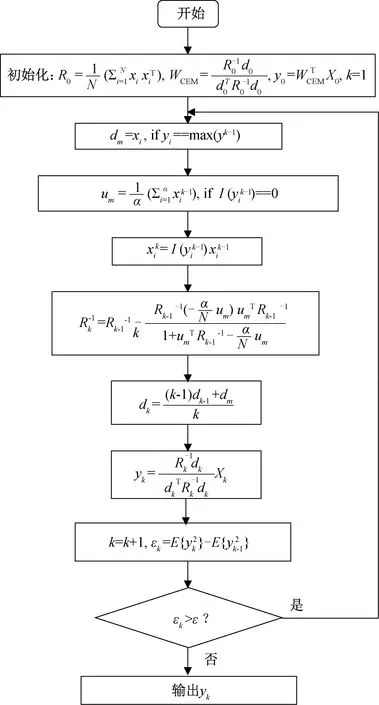
图1 基于增量学习的约束能量最小化算法流程Fig.1 Flow chart of CEM based on incremental learning

3 实验结果及分析

实验环境统一为CPU频率为1.1 GHz的PC机，算法运行在Matlab 2016b上。实验中的超参数都统一设置为λ=200，ε=10-5。本文方法将与CEM[10]、SAM[5]、ACE[7]这3种方法进行对比，从仿真图像、真实图像、算法时间复杂度这3个方面来验证其有效性。

3.1 仿真高光谱图像实验

本实验所用的仿真高光谱图像是通过美国地质调查局(USGS)数字光谱库得到的。USGS光谱数据共包含224个波段，光谱范围是0.4～2.5 μm。该图像中包含15种物质的光谱，两个目标。实验加入了信噪比为30 dB的高斯白噪声以检测算法的鲁棒性。图2(a)显示了该高光谱仿真图像的第一波段，图2(b)则为其中目标的真实分布，图2(c)～图2(f)分别为CEM、SAM、ACE和本文提出的算法，为了便于比较，4种算法的输出都被归一化到0～1之间。可以看到CEM和SAM算法检测失败，ACE算法仍然有很多的虚假目标被检测，而本文方法最大程度地抑制了背景光谱，降低了虚警率，具有更好的检测效果。

图2 不同算法在仿真高光谱图像上的检测结果Fig.2 Detection results of various algorithms on simulated hyperspectral images

ROC曲线描述了目标检测中虚警率与检测率之间的变化关系，当虚警率相同时，算法的检测率越高则性能越好。图3给出了4种算法的ROC曲线，可以看到本文的ROC曲线更加靠近左上角，ROC曲线下的面积最大，因此本文的算法检测性能最好。

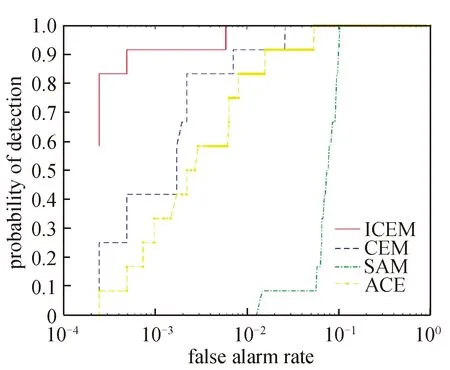
图3 在仿真图像上的ROC曲线Fig.3 ROC curves of various algorithms on simulated hyperspectral images

3.2 真实高光谱图像实验

真实高光谱图像采用美国圣地亚哥机场的AVIRIS图像，该图像是采用机载可视/红外成像光谱仪拍摄，共有224个波段，波段范围是0.4～2.5 μm，图像中包含了3个飞机目标。实验中实际使用其中的189个高信噪比的波段。图4显示了对真实图像的检测结果，其中，图4(a)为图像的第一波段，图4(b)为其中目标的真实分布，图4(c)～图4(f)分别为CEM、SAM、ACE和本文提出的算法，结果同样被归一化到0～1区间。可以看到SAM算法检测失败。CEM虽然在目标处有比较强的响应，但背景光谱抑制得不干净，有许多背景噪声。ACE算法过度抑制了噪声光谱从而出现目标丢失现象，而本文方法能够很好地抑制背景并成功检测出目标。

图5为4种算法在该真实图像上的ROC曲线。可以看出，本文算法的曲线拥有最大的曲线下面积，检测效果最好。

图4 不同算法在真实图像上的检测结果Fig.4 Detection results of various algorithms on real hyperspectral images

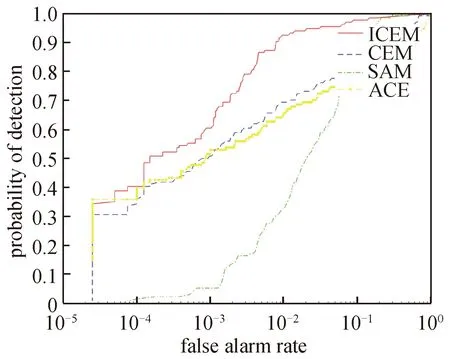
图5 在真实图像上的ROC曲线Fig.5 ROC curves of various algorithms on real hyperspectral images

3.3 时间复杂度

运行时间是衡量算法性能的重要方面，尤其在星上处理时，对算法时间的要求更加迫切。表1显示了4种算法在仿真图像与真实图像上的运行时间。由于本文方法是采用CEM算法进行目标初始检测，在此基础上通过增量学习得到最终检测结果，因此本文方法的运算时间可分解为初始检测时间(CEM算法的时间)和增量学习过程所用的迭代时间。可以看出，本算法作为CEM算法的增量学习版本，在以CEM算法作为初始迭代的情况下，仿真图像上的耗时仅比CEM算法高出0.015 s，实际图像上的耗时比CEM高出0.047 s，同时总用时远低于其他两种算法。这说明后续几次增量迭代所需的时间消耗是很低的。增量迭代用矩阵相乘代替自相关矩阵的求逆，矩阵求逆的复杂度为Ο(L3)，而矩阵乘法的复杂度为Ο(L2)。因此，本文算法的复杂度得到了数量级的减弱，有效减少了计算资源的消耗。

表1 不同算法的运行时间

4 结论

本文提出了一种基于增量学习的约束能量最小化算法，利用Sherman-Morrison定理，不需要重新计算自相关矩阵的逆矩阵即可更新滤波器权重，有效减少了算法的计算复杂度。此外，通过仿真高光谱图像与真实高光谱图像的实验，算法的检测精度较传统高光谱目标检测算法有明显提升。因此本文算法在精度与速度层面都取得了满意的效果，有望在星上计算资源有限的条件下得到实际应用。