知识系统决策规则的动态更新策略及等价矩阵计算

谭天乐

(1.上海航天控制技术研究所，上海 201109； 2. 上海市空间智能控制技术重点实验室，上海 201109)

0 引言

航天是人工智能技术应用的重要领域，而人工智能在航天的应用可以追溯到20世纪70年代。航天领域中的人工智能系统有很大一部分是基于“符号主义”路线建立的各种专家系统。例如：针对深空探测，NASA在“旅行者”深空探测器上构建了一个包含140余条规则的专家系统DEVICER II[1-2]以快速执行行星观测任务，“好奇号”火星探测器采用专家系统自主引导相机进行巡视探测；针对航天飞机，NASA先后开发和应用了液氧推进剂装填专家系统(LOX)、发射前专家系统(PLES)、智能化信息管理系统(IMIS)、基于知识库的自动测试系统(KATE)、发射过程专家系统(LPS-I)，货仓规划使用专家系统(EMPRESS)等；针对空间站，NASA研制了用于环境控制与生命保障专家系统FIXER，我国航天医学研究所提出了空间站内基于专家系统的人机混合智能系统[3]；在空间遥感观测上，美国的“地球观测一号”卫星可以进行地表观测目标的自主寻找与价值评估；此外也有学者研究了如何在航天器飞行任务规划中采用专家系统[4]。

专家系统从逻辑思考、表达方法上模拟人类智能活动，基于数学逻辑和推理，实现知识的表达、应用，其主要形式为规则集或规则库，是人工智能“符号主义”路线的主要理论方法。在专家系统中，知识获取、规则生成通常依靠专家经验的总结归纳，知识的学习一直以来是瓶颈问题，在定量分析上专家系统也面临困难。

专家系统作为人工智能的重要理论基础和应用技术方法，需要具备自主的知识学习能力，能够根据学习样例的变化进行知识的动态自适应学习和更新。在一个以决策规则形式进行知识表达的信息系统中，当产生决策规则的学习样本发生动态变化时，知识库中的决策规则需要相应进行调整。如果在样本集发生变化后对信息系统的所有样本进行整体的规则获取，因没有充分利用过去所获得的知识，将导致大量不必要的重复运算。因此需要解决当知识系统中样本发生变化时，基于已有决策规则进行决策规则动态学习和调整的问题。

在对知识系统进行属性约简以及求核上，常见的方法有基于区分矩阵/差别矩阵[5-6]、遗传算法[7]等等。在对知识系统中所有样本进行决策规则的值约简，获取全局决策规则上，国内外已经提出了多种方法[8-10]。在决策规则的动态更新上，文献[11-17]分别介绍了基于区分矩阵、决策矩阵、基于元信息、基于专家先验知识等几种规则动态更新算法或其改进。但这些方法在规则更新过程的知识表达、存储和计算上仍然不够简洁，有些还需要依赖先验的知识，且讨论仅限于样本增加情况下的规则更新，没有分析移除学习样本的情况。

本文在基于决策规则的知识系统中，分析并提出了基于已有的样本和决策规则，根据学习样本增/减对决策规则进行动态调整的策略，结合布尔运算提出了知识系统决策规则动态更新的矩阵算法，讨论了方法的完备性和一致性，并给出了一个仿真例，验证了方法的有效性。

1 知识系统决策规则的动态调整逻辑

1.1 知识系统及决策规则的表示

用四元组S=(U,R,V,f)来表述一个知识系统，其中U={x1,x2,…,xn}为一个非空有限的样本集合，称为论域。集合中的样本xj使用属性ri∈R和相应的属性值vij∈Vri来描述，Vri是属性ri的值域集合。属性值集合V=∪Vri，(ri∈R)。f：U×R→V是一个计算函数或计算方法，它为每个样本的每个属性赋予一个信息值，即x∈U，∀ri∈R，f(x，ri)∈Vri。一个属性又称之为一个等价关系。

在知识系统中将样本根据条件属性及其取值进行特征描述，按照决策属性及其取值进行分类。将特征与分类进行对应成为决策规则。知识系统中存在一个最小化的决策规则集，规则集是学习样本所支持的所有决策规则的约简，任意一条决策规则均不存在多余的属性描述，规则集中的决策规则不存在冗余和矛盾，满足协调一致性，任意两条决策规则的条件不存在包含关系。

知识系统用决策表的形式表示，决策表的列为属性，行为样本。属性集合R=C∪D，C∩D=Ø，C为条件属性子集，用于描述样本特征，D为决策属性子集，用于描述样本分类。

1.2 新增学习样本时的决策规则调整

知识系统中的决策规则来自于论域空间中的样本。新的学习样本带来新规则，某些旧规则因与新样本冲突而需要被移除。

若U0为初始论域，Rold为其最小化决策规则集，Unew为新增样本集合，则U=Unew∪U0为新论域。样本新增及其规则调整的方法如下：

步骤1：从Rold中找出与Unew中任一样本矛盾和匹配的规则，将它们从规则集Rold中移除，并将矛盾的规则记录在规则集Rconf中。

移除与Unew中任一样本匹配的规则，是避免后续从Unew中获取的规则冗余。

步骤2：从U0中找出匹配Rconf中任一规则的样本记录在集合U′0中，并将它们从U0中移除。

Rconf中的规则虽然被新样本否定，但生成这些规则的样本在其他属性上加强一下，将可能产生新的规则，需要重新进行规则获取。

步骤3：从规则集Rold中再次移除匹配U′0中任一样本的规则。

该步骤将避免与后续从U′0中获取的规则冗余。

步骤4：顺序排列Unew、U′0及步骤2得到的U0，以后述矩阵计算获取Unew∪U′0在U中所能够产生的新增规则集Rnew。

Rold∪Rnew构成U的最简规则集Rend。其中Rold为步骤3的结果。

在样本增加后调整规则集的方法中，步骤1使得最终的规则集与新增样本不矛盾。步骤2找到U0中受新增样本各属性取值约束而需要重新进行规则获取的样本集合U′0。步骤3将Rold中匹配U′0的规则移除以避免与步骤4的结果产生冗余。步骤4对新论域中的新增样本Unew及所有可能需要重新获取决策规则的样本U′0在新论域U中进行规则获取，从而保证了不会产生规则的遗漏。因此最终的规则集不存在冗余、遗漏和不一致。

对于新增样本时的规则调整的特例，当初始论域为空，新论域完全由新增样本构成时，规则调整的方法成为对整个论域空间进行规则获取的全局算法[10]。

1.3 移除学习样本时的决策规则调整

论域中学习样本的减少同样也将导致规则集合的变化。因为学习样本的移除，一些规则相应的失去了支持依据。同时，移除的样本可能解除了某些约束。

令U0为初始论域，Rold为其最小化决策规则集。Umov为移除样本集合，U=U0/Umov为新论域。样本移除及其规则调整的方法如下：

步骤1：从Rold中找出匹配Umov中任一样本的规则，将它们从Rold中移除；

步骤2：在U中寻找至少在一个条件属性值上与某移除样本相同的样本记录在U′中，并将它们从U中移除。

任一保留样本与任一移除样本之间在属性取值上有：

1)所有条件属性值均不相同，决策属性值或者相同或者不相同。此类保留样本产生的决策规则与移除样本产生的决策规则不可能在规则前部上相同，因此这类样本不需要重新获取规则。

2)至少有一个条件属性值相同，决策属性值相同或者不相同。此类保留样本中，又有决策属性值与移除样本不一致和一致两种。前者是移除样本解除了在取值相同的条件属性上的约束，需要对这些样本重新进行规则获取。后者是移除样本解除了在取值不同的条件属性上的约束，需要对这些样本重新进行规则获取。综上，对于此类样本，都需要重新进行规则的重新获取。

步骤3：从规则集Rold中再次移除匹配U′中任一样本的规则。通过该步骤避免与后续从U′中获取的规则冗余。

步骤4：顺序排列U′及步骤2得到的U，以后述矩阵计算获取U′在U中所能够产生的规则集Rnew。

Rold∪Rnew构成论域U0/Umov的最简规则集Rend，其中的Rold为步骤3的结果。

步骤1使得最终的规则集中不存在仅由移除样本产生的规则。步骤2找到受移除样本属性取值约束的样本。步骤3将Rold中匹配U′的规则移除以避免与步骤4的结果产生冗余。步骤4对所有可能需要重新获取决策规则的样本U′在新论域U中进行规则获取，从而保证了不会产生规则的遗漏。因此最终的规则集不存在冗余、遗漏和不一致。

2 从部分样本中获取规则的矩阵计算

这里给出在论域U中获取其子集U′⊆U所支持的决策规则的等价矩阵计算，该算法是文献[10]中矩阵算法的改进，在规则获取上更加具有一般性。

2.1 等价矩阵[18]

首先定义等价矩阵。令S=(U，R，V，f)为一个知识系统，样本子集U′⊆U，样本xi∈U′，样本xj∈U，样本子集的样本数Card(U′)=m≤n=Card(U)。

定义1：属性C⊆R的m×n维等价矩阵MC=[aij]，MC中的元素aij取值为

式中：i=1，2，…，m；j=1，2，…，n。

即对于样本xi、xj，如果两个样本在属性或属性组合C⊆R上的属性值一致，即该两个样本在属性或属性集合C上存在不可区分关系(等价，表示为EC)，则等价矩阵MC|m×n的i行j列元素为1，否则为0。

定义2：令M1=[aij]，M2=[aij′]分别为两个属性(或属性组合)m×n维等价矩阵。等价矩阵M1与M2的交集M1∩M2定义为M1∩M2=[bij]，其中bij为aij与aij′的二元与。

以上定义的矩阵与运算具有以下性质：结合律((M1∩M2)∩M3=M1∩(M2∩M3))、交换律(M1∩M2=M2∩M1)和幂等性(M1∩M1=M1)。

对于知识系统S=(U，R，V，f)，属性(或属性子集)C1，C2⊆R，m×n等价矩阵MC1={aij}，MC2={aij′}，MC1∪C2={bij}满足MC1∩MC2=MC1∪C2，即

该等价关系构成了决策规则获取的等价矩阵计算的基础。

2.2 规则获取矩阵计算

决策规则的前部可以是条件属性的各种不同组合。若样本由q个条件属性进行描述，不难得到，q个属性的所有组合的数目为Cq1+Cq2+…+Cqq=2q-1。例如4个属性{a，b，c，d}，各阶组合为：

1阶组合：{a}、{b}、{c}、{d}；

2阶组合：{ab}、{ac}、{ad}、{bc}、{bd}、{cd}；

3阶组合：{abc}、{abd}、{acd}、{bcd}；

4阶组合：{abcd}。

因此具有4个条件属性的知识系统的决策规则在规则前部上有24-1=15种形式。

利用Steinhaus-Johnson-Trotter算法[19]，可以找到条件属性的所有组合形式。

将包含的条件属性的数目为k的决策规则称为k阶决策规则，将涉及属性数为k的等价矩阵称为k阶等价矩阵。

利用等价矩阵对样本子集U′(m个样本)在整个样本集U(n个样本)中，从条件属性(或属性集合)C1⊆C上进行规则获取的步骤如下：

步骤1：逐一比较U′中每个样本i与U中每个样本j在C1上的取值，计算生成k(k=Card(C1))阶条件属性等价矩阵MC1|m×n。逐一比较U′中每个样本i与U中每个样本j在决策属性D上的取值，计算生成决策属性等价矩阵MD|m×n。

步骤2：依次对矩阵MC1、MD第i(i=1～m)行的行向量进行与运算。

1)如果与运算的结果不为全零向量且与MC1第i行行向量相等，以样本xi的属性C1，D的取值生成规则：

&(c=vc)⟹ &(d=vd)，c∈C1，d∈D。

依次判断aij∈MC1(j=1～m)是否为1，若是，将MC1第j行置全“0”。

2)如果与运算的结果为全零向量或与MC1第i行行向量不相等，下一行。

该步骤是通过比较判断：当样本i在C1上的取值与样本j一致(aij=1，不可区分、等价)时，其在D上的取值是否同样与样本j一致，且在整个论域中是否具有一致性。若成立，则得到决策规则。同时，为了避免在生成该规则后，在后续利用(k+1)阶等价矩阵获取涉及更多属性的(k+1)阶规则时，产生规则前部存在包含关系的决策规则，在生成该规则后，对k阶条件属性等价矩阵进行调整。

矩阵计算将U′中所有包含条件属性C1的决策规则获取出来，规则涉及的条件属性数为k(k=Card(C1))。

经过矩阵计算，k阶条件属性等价矩阵MC1更新为MC1new。

2.3 高阶决策规则的逐步获取

为了避免决策规则的条件部分存在相互包含，需要从1阶决策规则开始，逐步获取高阶决策规则。

由前述，(k+1)阶条件属性等价矩阵可以由k阶条件属性等价矩阵的与运算生成。在获取k阶决策规则过程中，k阶条件属性等价矩阵会因为规则的获取发生变化，因此，仅1阶条件属性等价矩阵是通过逐一比较样本子集U′中每个样本与样本全集U中每个样本在条件属性上的取值得到。后续的高阶条件属性等价矩阵均由更新之后的低一阶条件属性等价矩阵生成。

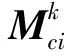
例如4个条件属性{a，b，c，d}，各阶条件属性等价矩阵的递阶生成关系如图1所示。

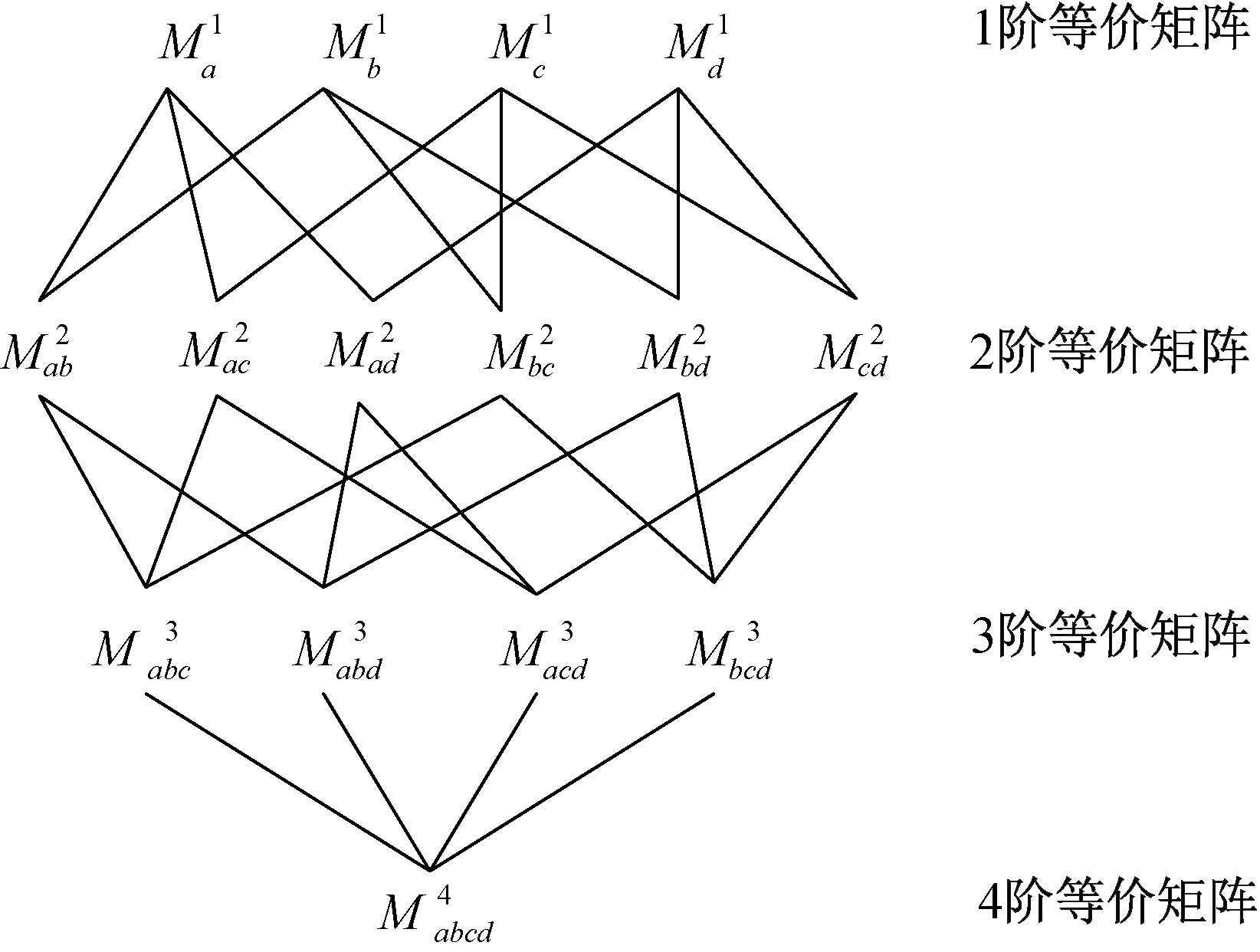
图1 条件属性等价矩阵的递阶生成关系Fig.1 Hierarchical generation relation of conditional attribute equivalent matrix

其他更多条件属性情况下等价矩阵的递阶生成关系依此类推。

3 计算复杂性分析

知识系统决策规则动态更新的方法和矩阵计算能够减少不必要的计算量。通过分析可知，决策规则动态更新的矩阵的计算复杂度是O(m×n×2Card(C))。计算量的增长对需要重新获取规则的样本的个数是多项式的，对条件属性个数是指数形式的。

对于决策规则动态更新的特例，当论域完全由新增样本组成时，新增样本时的决策规则调整便成为决策规则获取的全局计算，其计算复杂度为O(n2×2Card(C))。

通常由于需要重新进行规则获取的样本数量m≪n，与决策规则的全局获取相比，本节提出的规则动态更新的方法及矩阵计算可以大为减少计算量。

4 仿真示例

1)增加样本后的规则调整与矩阵计算

表1为一个包含5个样本的粗糙集信息系统U0={x1，x2，x3，x4，x5}。条件属性为a、b、c，决策属性为d。

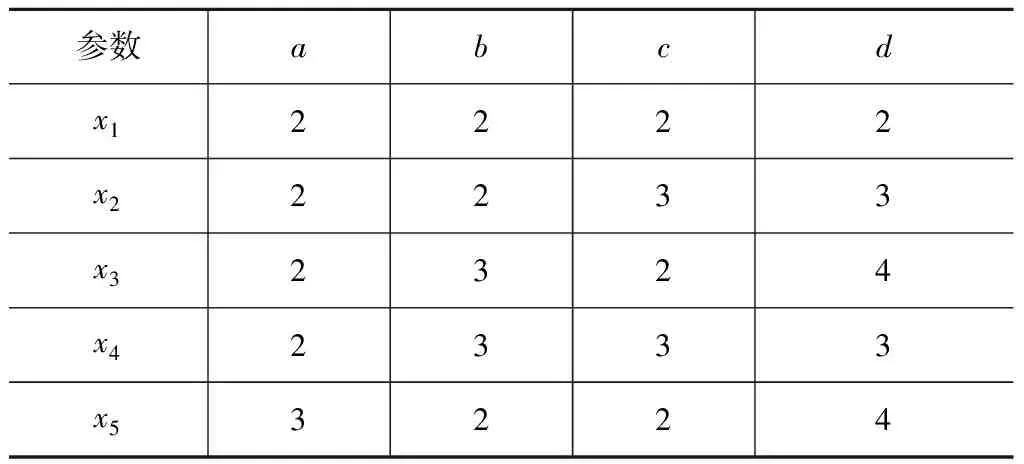
表1 初始论域U0

初始的最简决策规则见表2。

表2 初始规则集Rold

设新增样本集合Unew={x6}，进行增量规则调整，见表3。

表3 新增样本集合Unew

步骤1：从Rold中移除与新增样本Unew矛盾和匹配的规则。找到{②，④}，将矛盾规则记录为Rconf={②，④}。

步骤2：从U0中移除与Rconf中规则相符的样本。找到U′0={x2，x4，x5}。

步骤3：从规则集Rold中再次移除匹配U′0中任一样本的规则。本例无。

步骤4：顺序排列Unew、U′0及调整后的U0={x1，x3}，构成U={x6，x2，x4，x5，x1，x3}，开始采用矩阵计算获取Unew∪U′0在U中所能够产生的新增规则集Rnew。

首先生成1阶条件属性等价矩阵Ma、Mb、Mc和决策属性等价矩阵Md：

进行1阶决策规则的获取。分别用1阶条件属性等价矩阵与决策属性等价矩阵进行与运算，得到如下3个矩阵：

依次分别比较Mad和Ma、Mbd和Mb、Mcd和Mc的相同每一行以获取规则，没能获取1阶规则。1阶矩阵Ma、Mb、Mc不变，MaNew=Ma，MbNew=Mb，McNew=Mc。构造2阶条件属性等价矩阵：

分别用2阶条件属性等价矩阵与决策属性矩阵Md进行与运算，得到如下3个矩阵：

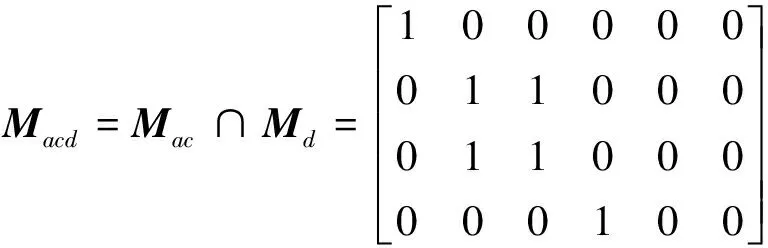
依次分别比较Mabd和Mab、Mbcd和Mbc、Macd和Mac的相同每一行以获取规则，利用Macd、Mbcd找到了2阶规则⑤～⑧，见表4。

表4 新增规则集Rnew

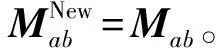
构造3阶条件属性等价矩阵Mabc为

等价3阶矩阵已经是全0矩阵,无法再进一步获取规则。增量规则获取过程结束。

Rold与获得的新增规则Rnew共同组成规则集见表5。

表5 最终的规则集Rend

2)移除样本时的规则调整与矩阵计算

表6为一个包含6个对象的粗糙集信息系统U0={x1，x2，x3，x4，x5，x6}。条件属性为a、b、c，决策属性为d。

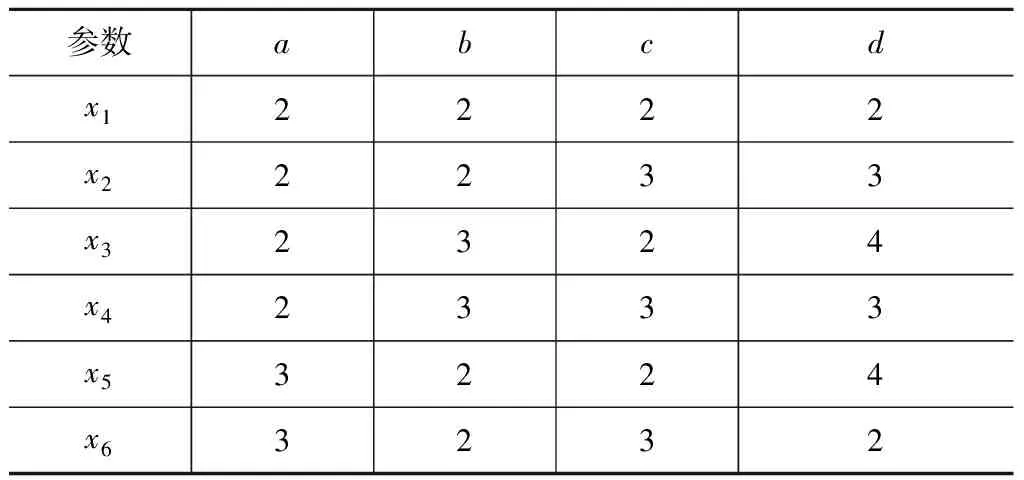
表6 初始论域U0

设待删除对象集合Umov={x3}。初始的最简决策规则见表7。

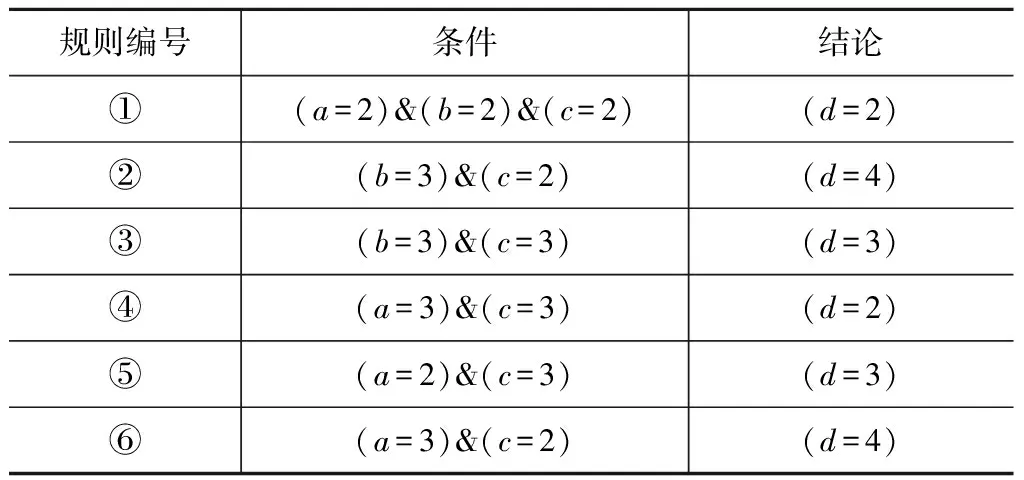
表7 初始规则集Rold

步骤1：从Rold中找出匹配Umov中任一样本的规则，找到规则{②}，将其从Rold中移除。

步骤2：在U=U0/Umov中寻找至少在一个条件属性值上与x3相同的样本，找到{x1，x2，x4，x5}，记录在U′中，并将它们从U中移除。

步骤3：从规则集Rold中再次移除匹配U′中任一样本的规则。移除规则{①，③，⑤，⑥}。

步骤4：顺序排列U′及步骤2得到的U，得到{x1，x2，x4，x5，x6}，开始采用矩阵计算获取U′在U中所能够产生的规则集Rnew。

首先生成1阶条件属性等价矩阵Ma、Mb、Mc和决策属性等价矩阵Md，分别为

进行1阶决策规则获取。分别用1阶条件属性等价矩阵与决策属性等价矩阵进行与运算，得到如下矩阵：

依次分别比较Mad和Ma、Mbd和Mb、Mcd和Mc的相同每一行以获取规则。利用Mbd从对象x4找到1阶规则，见表8。

表8 新增规则集

构造2阶条件属性等价矩阵，分别为

分别用2阶条件属性等价矩阵与决策属性矩阵Md进行与运算，得到如下矩阵：

依次分别比较Mabd和Mab、Mbcd和Mbc、Macd和Mac的相同每一行以获取规则，利用Macd找到了2阶规则⑧～⑩，见表9。

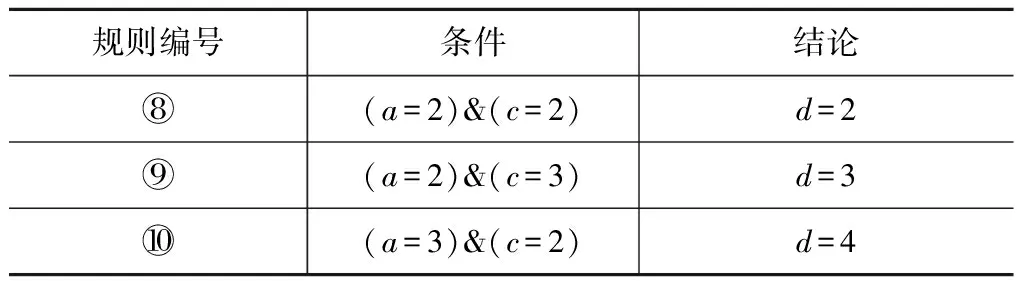
表9 新增规则

由于有规则产生，有

3阶条件属性矩阵已经是全0矩阵，无法再进一步提取规则。最终的决策规则见表10。

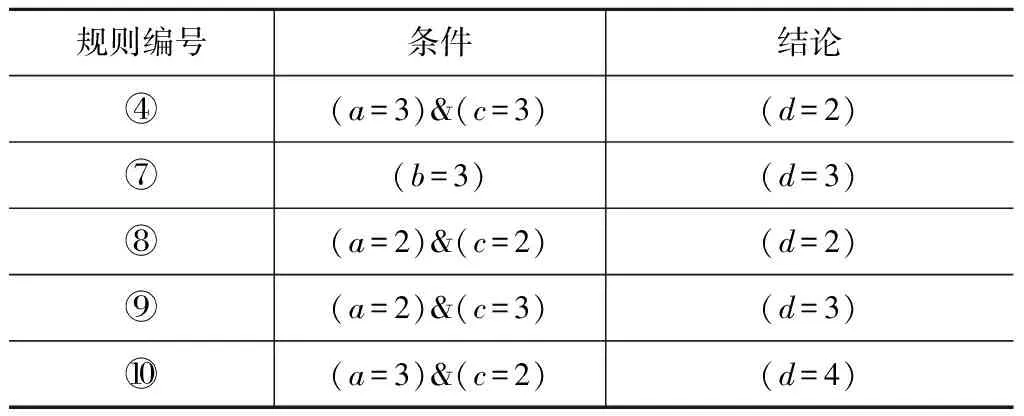
表10 最终的规则集Rend

5 结论

本文所提出的决策规则动态更新方法和等价矩阵计算方法使得知识系统具有了随样本变化进行自我学习和完善的能力，为专家系统、决策支持系统以及基于知识的控制系统等智能系统中知识的获取、动态调整提供了方法。使得专家系统在构建知识库时可以摆脱对专家经验知识的依赖，同时可以适应不断变化的大数据集，未来可以广泛应用于航天领域中信号分析、故障诊断、规划决策、操控与服务等专家系统的自动生成

由本文所介绍的方法可知，样本增加和移除情况下对决策规则集进行更新的逻辑和方法有较大的差异。移除样本时知识系统的调整更新策略更为复杂，意味着在知识系统中遗忘比学习的难度要大。

基于等价矩阵的矩阵计算将决策规则获取的过程与样本条件属性的物理含义及具体取值进行了分离，基于0、1布尔逻辑运算的决策规则获取过程在计算过程表达、数据信息存储、计算上较为简易方便和高效。计算的大部分过程都可以采用分布式存储和并行计算的方式完成。

文中所提出的方法对于冗余和不相容(矛盾)样本具有较好的鲁棒性。冗余的样本不会产生冗余的规则，矛盾的样本不会产生矛盾的规则。

当初始论域为空，新论域完全由新增样本构成时，决策规则的更新方法及等价矩阵计算成为对整个论域空间进行决策规则获取的全局方法。