一种多尺度稀疏极化敏感阵列及其DOA估计方法

丁 进，杨明磊，李曙光

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071；2. 上海航天电子技术研究所，上海 201109)

0 引 言

近几年，电磁矢量传感器(SS-EMVS)由于可同时提供目标信号的DOA信息和极化信息受到了广泛的关注。电磁矢量传感器属于极化敏感天线的一种，通常由3个正交的电偶极子和3个正交磁环构成[1]，分别接收目标信号的电场分量和磁场分量。为了利用电磁矢量传感器的特点，WONG等[1]研究了一种名为矢量叉积的特殊算法，可估计目标的二维DOA和极化参数，然而由于电磁矢量传感器中各个电偶极子和磁环的相位中心重合，电磁分量之间的互耦严重影响了该算法的性能。2011年，WONG提出了一种双平行线结构的分离式电磁矢量传感器[2]，降低了电磁分量间的互耦，同时确保了矢量叉积算法的有效性。此后，多种形式矢量传感器和对应的算法也相继出现[3-5]。

在阵列信号处理中，DOA的估计精度与阵列孔径成正比。为了避免相位模糊，一般情况下阵元间距不可大于目标信号的半波长[6]。因此，大的阵列孔径往往需要更多的天线阵元。但天线间的互耦和整个阵列的成本也随之增加。为解决这个问题，诸多学者研究了多种稀疏阵列形式和对应的DOA估计算法，其中一类稀疏阵列由多个空间分离的子阵构成，利用不同基线长度的子空间旋转不变(ESPRIT)算法来实现DOA估计[7-10]，而另一类是为得到尽可能多的自由度(degree-of-freedom, DOF)以解决目标个数多于阵元个数的问题，如最小冗余阵列[11]、嵌套式阵列[12]和互质阵列[13]，这类DOA估计算法的重点在于利用阵列接收数据的高阶统计量来提高DOF，因此往往需要比较大的计算量。

近年来，极化敏感阵列作为一种具有相当潜力的新体制雷达，可以在阵列空域信息的基础上添加极化域信息，从而改善阵列在多维参数估计、抗干扰能力、检测的稳定性等方面的性能。得益于这些优势，诸多文献对其阵列方式及参数估计方法，以及多种电磁矢量传感器和稀疏阵列的结合方式开展了一系列研究[14-16]，已成为阵列信号处理领域的研究热点。如：文献[14]提出了一种嵌套式矢量传感器阵列，使用张量实现了目标DOA的估计；文献[15]提出了一种新的稀疏矢量传感器阵列；文献[16]提出了一种嵌套式的偶极子阵列，但这些阵列的阵列单元都是共点式电磁矢量传感器，电磁分量之间的互耦仍然很严重，整个阵列的成本和冗余也比较高。

本文提出一种分离式电磁矢量传感器组成的多尺度稀疏极化敏感阵列，以SS-EMVS为阵列单元进行稀疏布阵，在扩展阵列孔径的同时保持了电磁矢量传感器的完整特性，并设置2个阵元间距，将整个阵列分为2个均匀子阵，从而将电磁矢量传感器可收集目标信号完整电磁信息的特点和稀疏阵列在大孔径和低互耦上的优势进行了充分的结合。在该阵列形式下，对SS-EMVS利用矢量叉积算法可以得到目标方向余弦的无模糊粗估计值，对2个均匀子阵利用ESPRIT算法可以得到方向余弦的多个高精度模糊估计值，最后利用2级解模糊的方式得到目标方向余弦的高精度无模糊的估计值，结合三角运算，便可以得到2维DOA的高精度估计。而且上述过程中没有用到类似嵌套式阵列[12]中的处理过程，不需要利用接收数据的高阶统计特性，因此本算法的计算量较小。

1 阵列结构及其信号模型

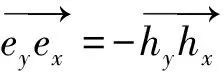
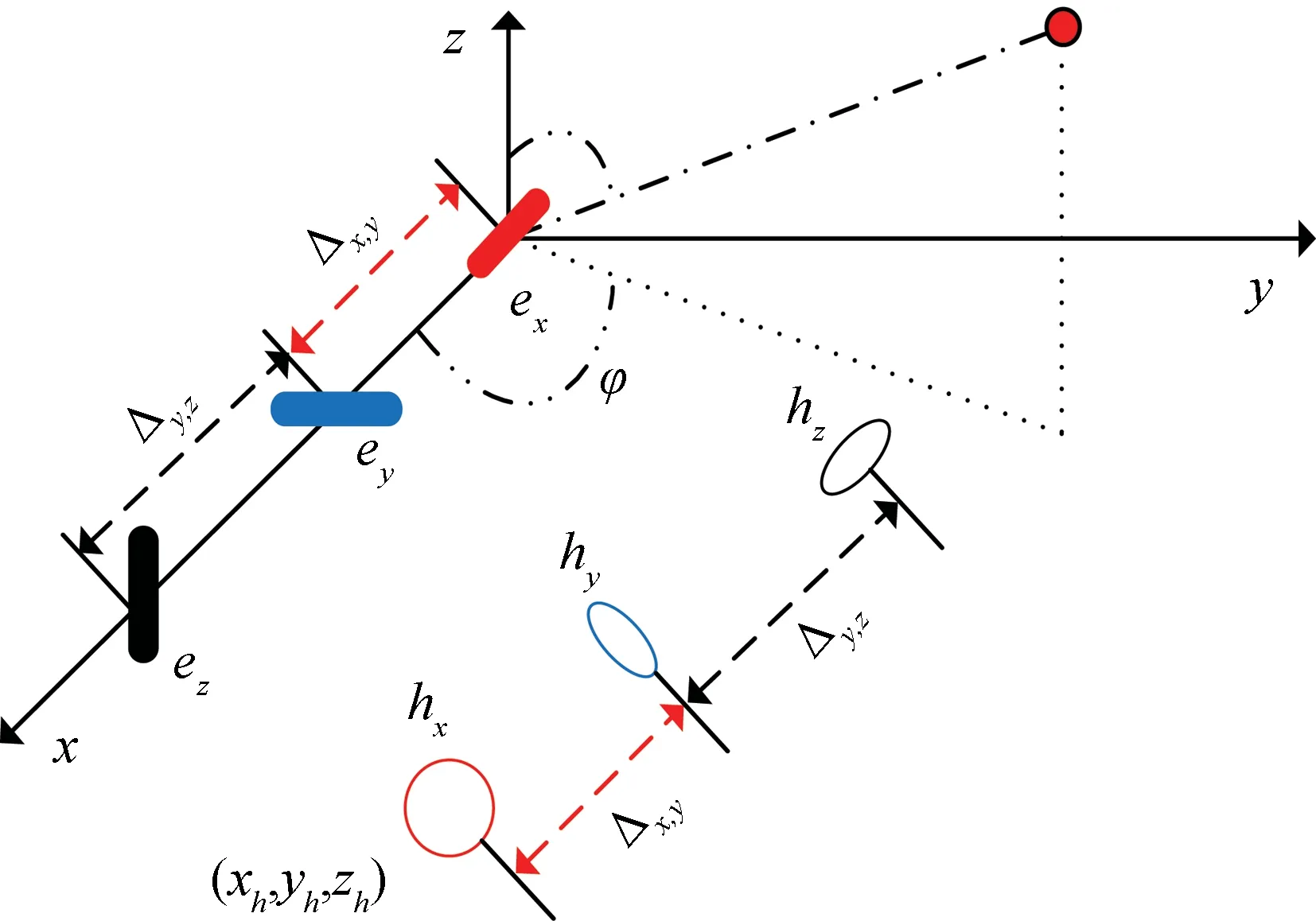
图1 分离式电磁矢量传感器结构Fig.1 Spatially-spread electromagnetic- vector-sensor configuration

该分离式电磁矢量传感器的导向矢量为

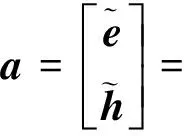
(1)

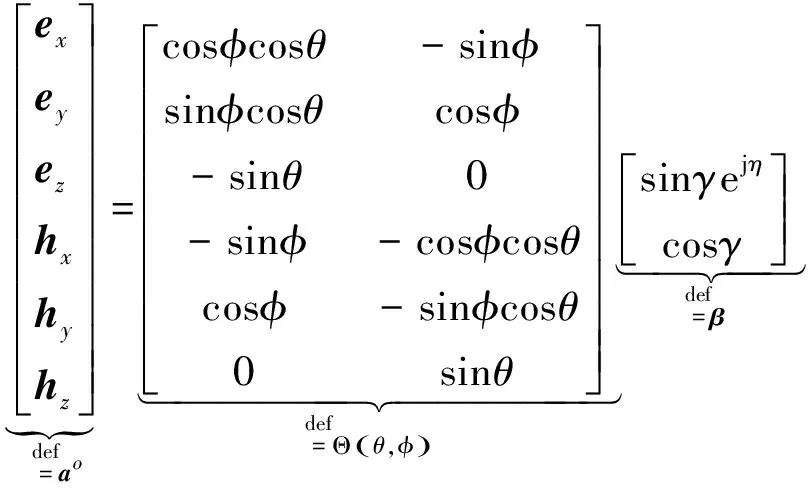
(2)

式中：(ex、ey,ez)分别表示x，y和z轴接收到的电场分量；(hx,hy,hz)分别表示x，y和z轴接收到的磁场分量;φ∈[0,2π)、θ∈[0,π]分别表示入射信号的方位角和俯仰角，方位角为信号与x轴正向夹角，俯仰角为信号与z轴正向夹角，γ∈[0,π/2]、η∈[-π,π]分别表示入射信号的极化辅角和极化相位差,u=sinθcosθ表示入射信号沿x轴的方向余弦，v=sinθsinφ表示入射信号沿y轴的方向余弦，w=cosθ表示入射信号沿z轴的方向余弦，⊙表示Hadamard积。

本文所提阵列如图2所示，阵列单元为图1的分离式电磁矢量传感器，沿y轴分布，前n1个阵元组成阵元间距为D1(D1>λ/2)的均匀线阵，为子阵1，剩余的n2个阵元以阵元间距D2(D2=mD1)组成子阵2，其中m表示大于1的整数。

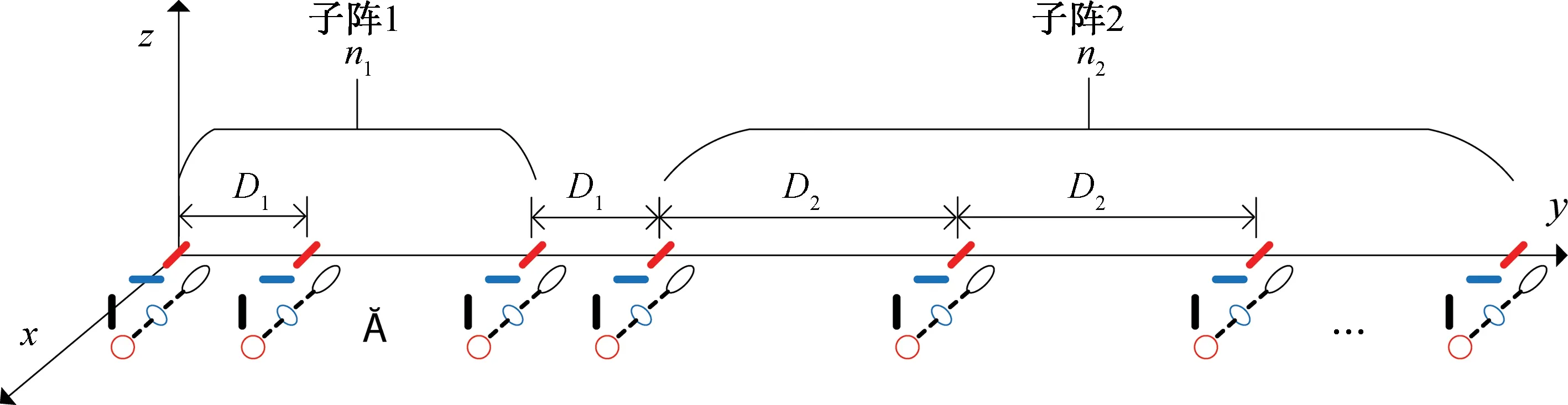
图2 多尺度稀疏极化敏感阵列Fig.2 Multiscale sparse polarization sensitive array

该阵列的阵列流型为

(3)

考虑K个相互独立的窄带信号入射到该阵列，则接收数据为

(4)

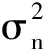
X=[x(t1),x(t2),…,x(tL)]

(5)

2 DOA估计算法

2.1 信号子空间矩阵的估计值

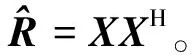
根据本文阵列的结构，将阵列流型B分为两部分：子阵1对应的B1和子阵2对应的B2。同理，将Es也按相同方式分为Es1和Es2，分别与B1和B2对应，即

(6)

2.2 u和v高精度但存在周期性模糊的估计值

由图2可知，整个阵列以不同的阵元间距分为2个子阵，即子阵1和子阵2。以子阵1为例，前n1-1个阵元和后n1-1个阵元可构成空域旋转不变性，表示为

(7)

式中:by1,1(k)和by1,2(k)分别表示第k个目标在子阵1前n1-1个阵元和后n1-1个阵元处的导向矢量，K个目标则可构成

By1,2=By1,1Φv,1

(8)

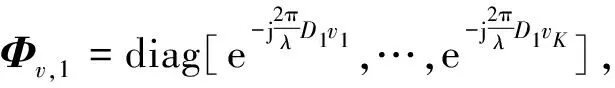
利用ESPRIT算法处理该空域旋转不变性，因D1>λ/2，可用总体最小二乘法解得一组高精度但存在周期性模糊的v估计值，即

(9)

式中：∠()表示()中元素的相位。

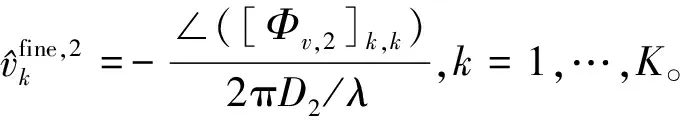
2.3 u和v的无模糊但低精度的估计值

根据式(6)得到子阵1和子阵2的阵列流型B1和B2的估计值，即

(10)

以ex位于原点的SS-EMVS为参考阵元，对所有电磁矢量传感器的导向矢量进行相位补偿，以便进行相干相加，从而合成到参考阵列单元处的SS-EMVS的导向矢量上，补偿量为各个电磁矢量传感器的相移因子，即

(11)

(12)

对式(12)的结果进行平均，作为参考阵元处SS-EMVS导向矢量的最终估计值，即

(13)

从式(13)可以得到(u,v)一组无模糊但精度较低的估计值，即

(14)

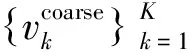
在得到u和v的粗估计值后，令p0=p⊙e-∠[p]1，有

(15)

在式(15)的基础上，可以得到1组精度相对较高但周期性模糊的u和v估计值，即

(16)

(17)

2.4 解模糊及DOA估计

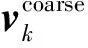
(18)

(19)

式中：l1的取值范围为

(20)

式中：「⎤和⎣」分别表示向上取整和向下取整。

(21)

(22)

l2的取值范围为

(23)

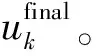
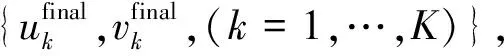
(24)

本文所提稀疏极化敏感阵列的DOA估计算法流程如图3所示。

3 仿真结果与分析

3.1 目标二维DOA估计与配对结果

设阵列单元数为12，前6个SS-EMVS组成子阵1，阵元间距D1=7λ，剩余6个以阵元间距D2=7D1=49λ构成子阵2。每个SS-EMVS都满足Δx,y=Δy,z=5λ。假设同一距离单元内存在K=2个相互独立的目标，俯仰角为θ=(42°,65°)，方位角为φ=(20°,52°)，极化辅角为γ=(45°,35°)，极化相位差为η=(40°,30°)。快拍数L=200，信噪比为15 dB。入射信号为随机信号模型，噪声为方差为0的复高斯白噪声。图4为200次蒙特卡洛实验的二维DOA估计结果，可以看出本文算法能够正确估计出目标的俯仰角和方位角且自动配对正确。

3.2 目标参数估计性能与信噪比的分析

图4给出了目标二维DOA估计结果，图5给出了本文算法中不同的u和v估计值的均方根误差与信噪比的关系。由图可见：ufinal和vfinal的估计精度比ucoarse和vcoarse要高很多，更接近参数估计的克拉美罗界(CRB)。另外，在解模糊过程中存在1个信噪比门限，当信噪比低于该门限时，估计性能迅速恶化，而当信噪比高于该门限时，估计精度也迅速提

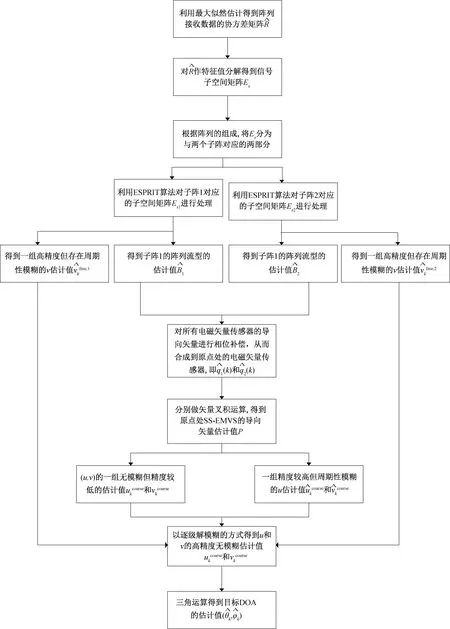
图3 DOA估计算法流程Fig.3 Flow of DOA estimation algorithm

高[18,21]。从图5可以看出u，v的信噪比门限分别是-7 dB和-3 dB，而且估计精度随着信噪比的提高而提高。

另外，以2个均匀线阵作为比较，设阵列单元个数都为12，阵元间距分别为D1和D2。图6给出了这3种阵列的u和v估计值与信噪比的关系。从图中可以看出，对于u，因为这3种阵列在x轴方向上的孔径完全一致，估计精度基本相同。而对于v，本阵列的阵列孔径处于这2个均匀线阵之间，估计精度也位于中间位置，但阵元间距为D2的均匀线阵的信噪比门限比本阵列高得多(13 dB)。

图4 目标二维DOA估计结果Fig.4 Two-dimensional DOA estimation results of targets

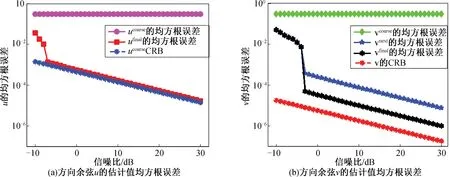
图5 方向余弦u和v的估计值均方根误差与信噪比的关系Fig.5 RMSE of direction cosines u and v estimations versus SNR

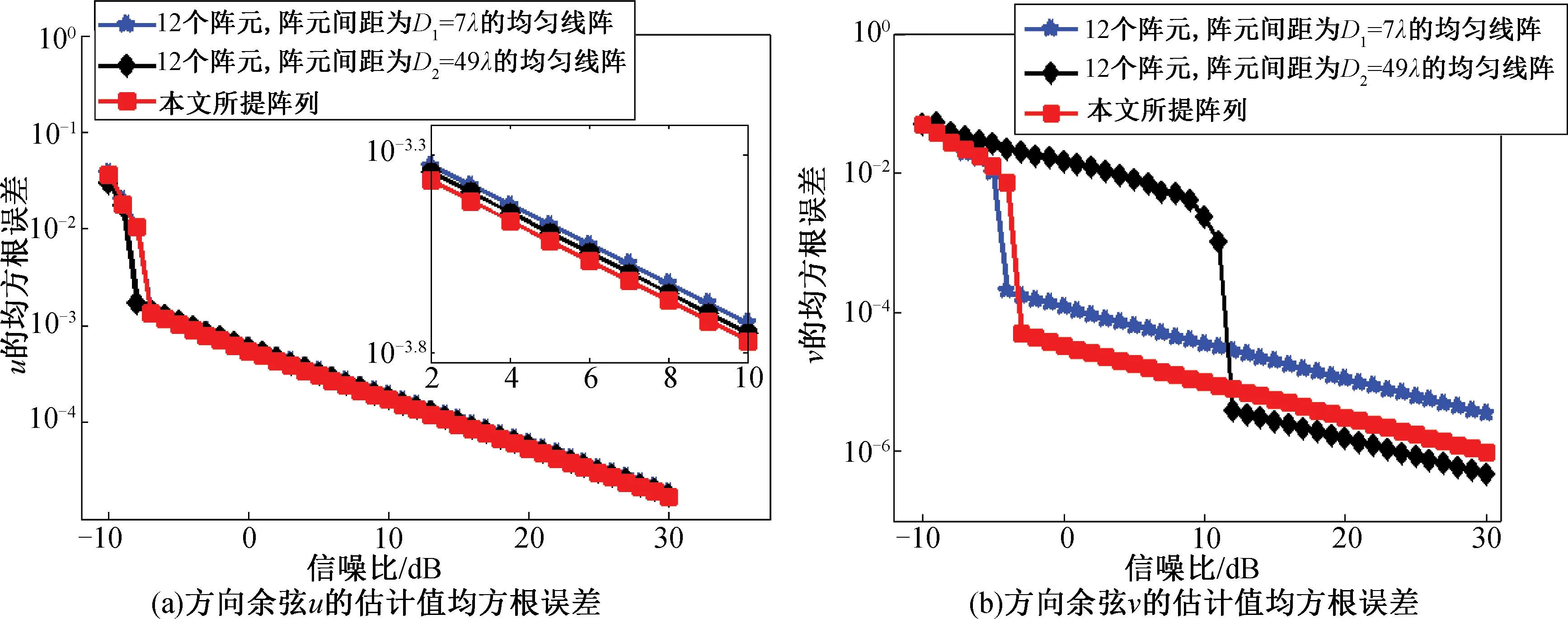
图6 不同阵列下方向余弦u和v的估计值均方根误差与信噪比的关系Fig.6 RMSE of direction cosines u and v estimations of different arrays versus SNR

3.3 目标二维DOA估计性能与信噪比的分析

由于目标的二维DOA信息由u、v共同决定，图7给出了俯仰角和方位角估计值的均方根误差随信噪比变化的曲线。由图可以看出：本阵列的信噪比门限为-3 dB，是u和v的门限中较大的一个。由于本阵列与对比阵列对u的估计精度基本相同，而DOA的估计精度又与u和v都有关，因此本阵列对DOA估计性能的提升并不明显，但仍可看出估计精度有所提高，且信噪比门限较低。

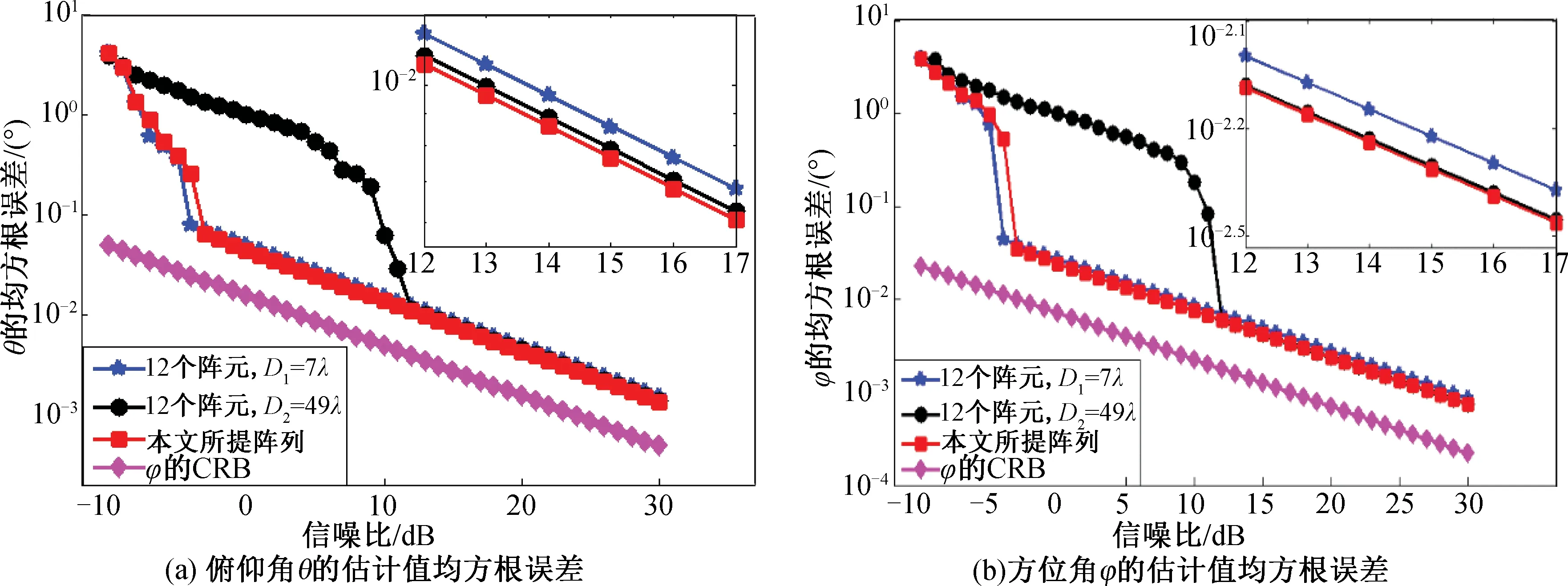
图7 不同阵列下俯仰角θ和方位角φ的估计值均方根误差与信噪比的关系Fig.7 RMSE of elevation θ and azimuth φ estimations of different arrays versus SNR

4 结论

本文提出了一种多尺度稀疏极化敏感阵列，并针对该阵列提出了对应的DOA估计算法。相比传统的共点式电磁矢量传感器，分离式结构可以显著降低阵元间互耦，降低硬件实现的复杂性。与均匀线阵的形式相比，该阵列在参数估计性能、互耦和对噪声的鲁棒性上具备更好的权衡效果。理论上，该阵列可扩展到更多子阵，以便在性能和成本上进行更合适的选择。后续研究中，拟针对线阵只能进行某一维上的孔径扩展的不足，研究该稀疏极化敏感阵列的L型阵，实现孔径的二维扩展；同时，对作为阵元的电磁矢量传感器进行结构简化，从而降低阵列成本。