基于随机活动工期的多模式现金流均衡项目调度优化

宁敏静， 何正文， 刘人境

(1.西安交通大学 管理学院，陕西 西安 710049; 2.过程控制与效率工程教育部重点实验室，陕西 西安 710049; 3.西南石油大学 经济管理学院，四川 成都 610500)

0 引言

在现实的项目管理领域，越来越多的项目呈现出投资规模大、实施周期长的特征。自身融资能力有限的承包商不能满足巨额投资资金需求。现金流均衡项目调度问题(CFBPSP，cash flow balance project scheduling problems)研究可以在一定程度上解决这一问题，通过合理地安排活动的开始时间，来实现项目现金流入与流出的动态均衡[1,2]。过长的周期导致项目在执行过程中有可能出现较多的不确定扰动，使之处于不确定环境中，通常表现为活动工期的变化性。基于随机活动工期的现金流均衡项目调度问题的研究，能够为不确定环境中的项目提供现金流尽可能保持均衡的进度计划，使承包商在项目执行过程中避免产生自身难以承受的资金缺口，从而保证项目的顺利实施[3,4]。

值得注意的是，在实际的项目执行过程中，在遇到不确定扰动时，承包商为了实现既定的计划安排，经常通过调整资源或资金投入量的方法来改变项目进度[5,6]。因此，本文研究基于随机活动工期的多模式现金流均衡项目调度问题，具有更为明确的现实背景，其研究成果能够为实际中的项目进度管理和现金流控制提供直接的理论支持。

纵观项目调度问题的研究[7～10]，不确定环境下项目调度问题的研究主要集中在时间维度，目标函数多是进度安排的鲁棒性，而关于资金维度的研究则不多，只有少数关于不确定条件下折现流项目调度问题(PSPDCF, project scheduling problems with discounted cash flows)的研究[11～13]。本文研究随机活动工期下的现金流均衡问题，充实了不确定环境中项目调度问题关于资金维度的研究。

1 问题界定及符号定义

本文采用AoN网络[14]表示项目。活动之间满足网络优先关系约束，活动开始时间不得早于其紧前活动的最晚结束时间。活动具有多种执行模式，不同模式对应不同的工期、费用。需要说明的是，受不确定因素的影响，活动在各模式下的工期为服从一定均值分布的随机变量，当活动完成后获得相应的挣值。合同总价款为所有活动的挣值之和。要求项目必须在计划截止时间之前完成。此外，对于在不确定环境下实施的项目来说，进度计划必须具有一定的稳定性。为了确保进度计划在执行过程中的稳定性，要求计划的鲁棒性不得低于一个设定的阈值，这可以通过对活动工期随机分布的估计，结合由计划截止时间和AoN网络所决定的总时间裕量，由项目管理者权衡决定。在项目开始时，业主首先付给承包商部分预付款，之后进行里程碑支付，规定最后一次支付安排在项目结束时刻。项目完工时，业主必须向承包商支付除质量保证金外的剩余合同价款，质量保证金在质保期满后再行支付。表1给出了文中用到的所有符号的定义。

表1 符号定义表

2 构建模型

2.1 优化模型构建

基于随机活动工期多模式现金流均衡项目调度问题的优化模型可构建如下：

(1)

(7)

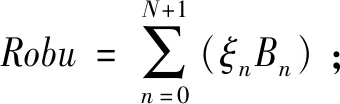
通过上述优化模型，便可在给定的多个约束条件下，借助对活动模式q及计划开始时间的安排，合理地调整项目的现金流入与流出以最小化现金流缺口，从而最大可能地保证项目现金流的动态均衡。在此需要特别说明的是，在上述优化模型中，约束条件式(5)和(6)之间实际上存在着如下内在联系：如果项目的计划截止时间D提前，则每个活动可调整的时间窗就会变小，所以，进度计划的鲁棒性也会随之下降。此时，若鲁棒性阈值设置得过高，则会造成问题模型无解。因此，项目管理者必须根据实际情况审慎地权衡两者之间的关系，以取得一个最佳的进度计划安排；否则，如果仅按照主观经验去决策，其甚至无法得到一个可行的进度计划安排。而本文所构建的调度优化模型，则为项目管理者的上述决策提供了一个直接的定量化分析工具。

2.2 问题的求解难度分析

在该模型中，通过令活动工期等于随机活动工期的均值，从而将不确定性项目调度问题转化为确定性项目调度问题。假定Robu*=0，η=1，即在给定的确定性项目调度条件下，项目执行过程中业主不对承包商进行任何支付，而在质量保证期满后进行一次性支付。这种情况下，Gmax必然发生在项目完工时刻，由此可将上述模型的目标简化为：

基于随机活动工期的多模式现金流均衡项目调度问题即可转化为时间/费用权衡问题的工期子问题[15]。该问题已被证明为强NP-hard[16]，因此，本文的研究问题也必然是强NP-hard问题。

3 算法

鉴于问题的NP-hard属性，本文采用模拟退火算法进行求解，该算法被证明是求解项目调度问题的高效算法[17～21]。分析可知模型中存在两个决策变量，分别为活动执行模式及活动开始时间，相应地，在邻点生成时有两个算子，两者之间存在如下关系：活动执行模式的确定不依赖活动开始时间安排；确定活动开始时间安排在活动执行模式选定之后，可以省略生成邻点时活动执行模式的可行性判断，提高算法搜索效率。根据此内在逻辑，采用嵌套的方式寻找满意解。

3.1 解的表示及初始可行解的生成

鉴于所研究问题中活动具有多种执行模式的特征，采用如下两个列表表示问题的解：

·执行模式列表ML：该列表由N+1个元素，第n个元素代表活动n选择的执行模式q。

·时间裕量列表SL：该列表由N+1个元素，第n个元素代表活动n的时间裕量εn(εn∈[0,Ln-En])，其中，En和Ln分别是活动n的最早和最晚开始时间，由CPM法计算得到。

依据上述解的表示方式，可按照下述迭代程序求得活动的开始时间：

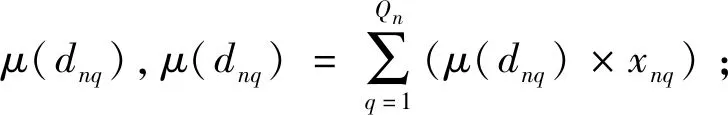
步骤2依据时间裕量列表SL，为各活动选择一个时间裕量εn，n=1,2,…,N；

步骤4应用CPM法计算得到活动的开始时间sn，n=0,1,2,…,N+1；

步骤5如果项目的结束时间超过截止时间sN+1>D，则对其目标函数进行惩罚，令Gmax=U；否则，生成一个可行的调度。

问题的初始可行解(MLini,SLini)按如下方式得到：首先，为每个活动随机分配执行模式，得到MLini，计算sN+1，若不大于D，则接受MLini。否则，重复该操作，直至得到可行的MLini。在时间裕量列表SLini上，将所有的εn都定义为0。

3.2 邻点生成机理

当前解(MLcur,SLcur)的邻点通过如下两个算子得到：

·模式变换(MC)算子：在MLcur上随机地选择一个活动(始末两个虚活动除外)，将其由当前执行模式列表MLcur中的执行模式变换为另外一种，在新模式安排下计算项目结束时间，如果不晚于项目截止日期D，则得到MLneig；否则，重复该操作直至获得MLneir。

·裕量改变(SC)算子：选择一个活动，将εn改变为[0,Ln-En]中的另一值，计算得到各活动的开始时间，若项目结束时间不晚于截止日期D，并且满足鲁棒性阈值约束Robu*，则得到SLneir；否则，重复该操作直至获得SLneir。

3.3 模拟退火参数设置

模拟退火算法中所涉及的一些参数设置如下，需要说明的是，在本文中内外两层嵌套中的参数设置相同。

·初始温度：初始温度Stempout、Stempin通过式子VGmax/lnPr：得到，其中VGmax是初始解的100个邻点中目标函数值的最大绝对差值，Pr是初始接受概率，设为0.97。

·退火速率：从初始温度开始，温度按照一定的比率μout(0<μout<1)、μin(0<μin<1)持续下降，均设为0.95。

·固定温度下的迭代次数：在某一固定温度下的迭代次数Num1、Num2均达到10×n时，进行降温处理。

·终止温度：温度降至终止温度Etempout、Etempin(等于0.1)时，算法终止。

3.4 算法搜索流程

模拟退火嵌套算法的搜索流程如下：

上述算法采用C++语言编程，计算实验在基于主频为2.1GHz英特尔处理器且内存为2048MB的个人计算机上运行。

4 实例

4.1 案例背景

本文所选实例是2008年中天集团有限公司总承包施工的一个CB大厦项目，位于西安市浐灞半岛，属于浐灞半岛开发的二期工程之一。CB大厦建筑面积66303平方米。项目总工期830天，合同总价款11451.7万元。项目采用AoN方式表示，见图1。项目包含39个活动(活动0和38分别为虚拟开始活动和结束活动)。活动具有加急和常规两种执行模式，由于施工过程中不确定因素的影响，两种执行模式下的活动工期均是服从一定均值分布的随机变量。活动在每种执行模式下的平均工期、工期标准差、费用及活动完成后得到的挣值见表2。预付款比例γ为7.5%，质量保证金比例η为7.5%，业主在12个里程碑活动3、5、7、9、11、13、18、25、31、33、36、38上对承包商进行支付，支付比例θ为85%。

为了保证随机活动工期下进度计划的稳定性，降低项目执行过程中因为计划改变所造成的调整成本，项目要满足一定的鲁棒性阈值约束。本案例中，项目的鲁棒性阈值Robu*由如下方法得到：首先，由计划截止日期D和AoN网络，应用关键路径法得到项目的总时差；其次，找到网络图中的所有路径，将总时差分配分别给各条路径上权重系数最大的活动，将总时差分配给这些具有最大权重系数的活动上，继而得到项目鲁棒性阈值Robu*的上界；同样地，将总时差分别分配给各条路径上权重系数最小的活动，继而得到项目鲁棒性阈值Robu*的下界；最后，在这个区间内取一个值Robu*=70作为项目鲁棒性阈值约束。

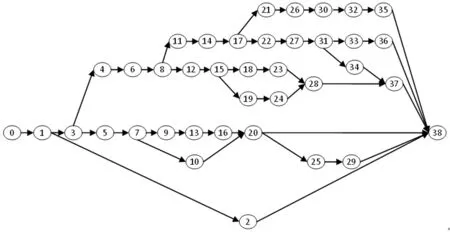
图1 CB大厦项目AoN网络图

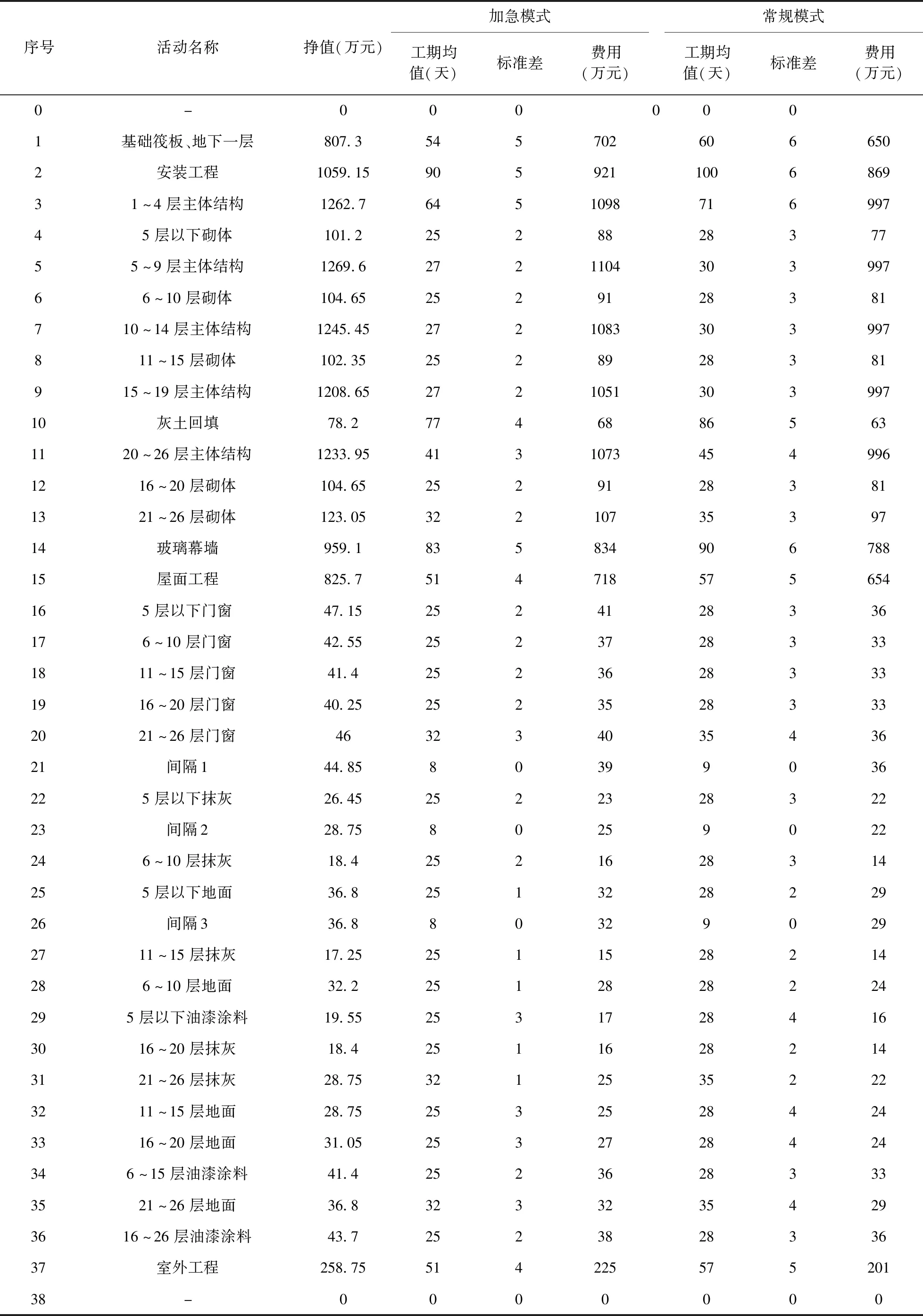
表2 项目参数表

4.2 理论结果与现实情况的比较

本文求解得到的项目满意进度安排如下:ML*=(1,2,2,2,2,2,2,2,2,1,1,2,2,2,2,2,2,2,2,1,2,2,2,1,1,1,1,2,1,2,2,2,2,1,1,1,2,1,1)，其中，1和2分别表示活动的常规和加急执行模式。

SL*=(0,0,363,60,131,192,159,286,187,344,399,215,226,386,260,257,449,350,322,342,544,378,385,397,625,387,406,436,651,395,434,423,469,469,451,494,494,679)

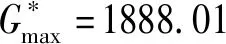
而在实际中，项目的进度安排如下：

ML0=(1,2,1,1,2,2,2,1,1,1,2,2,1,1,1,2,2,2,1,1,1,1,2,2,2,2,1,1,2,2,1,1,1,2,1,2,1,1,1)

SL0=(0,0,197,60,124,135,152,251,180,338,279,205,206,438,250,238,519,333,355,319,647,364,361,392,375,691,378,389,444,769,387,414,418,446,446,444,474,472,797)

G0max=3498.33(万元)

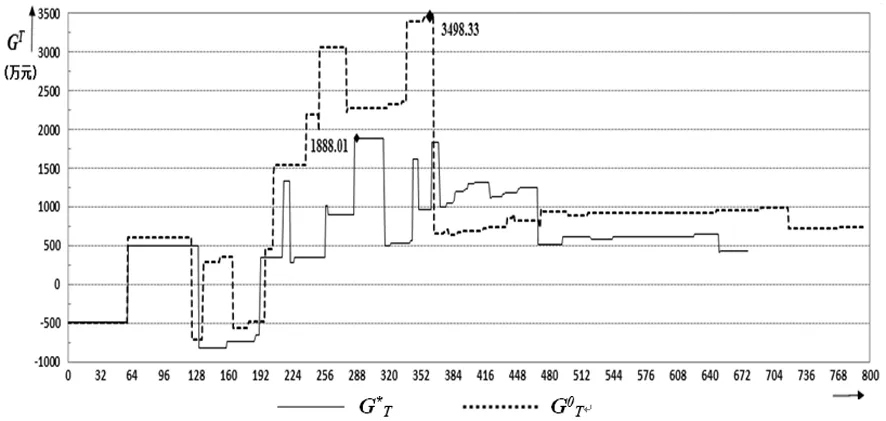
图2 承包商累计资金缺口GT随时间变化曲线

4.3 关键参数的敏感性分析

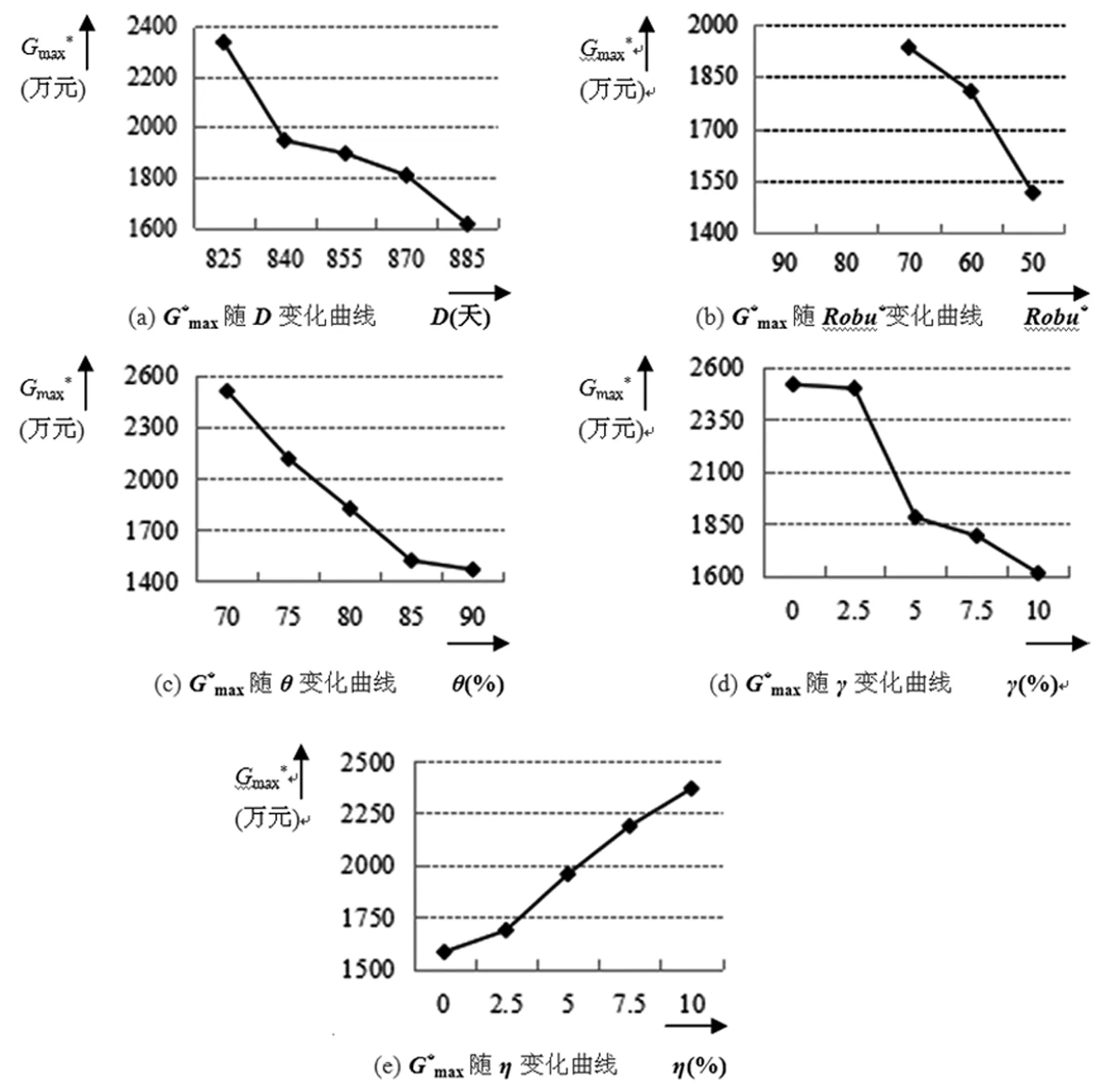
图3 承包商最大累计资金缺口随不同参数变化曲线

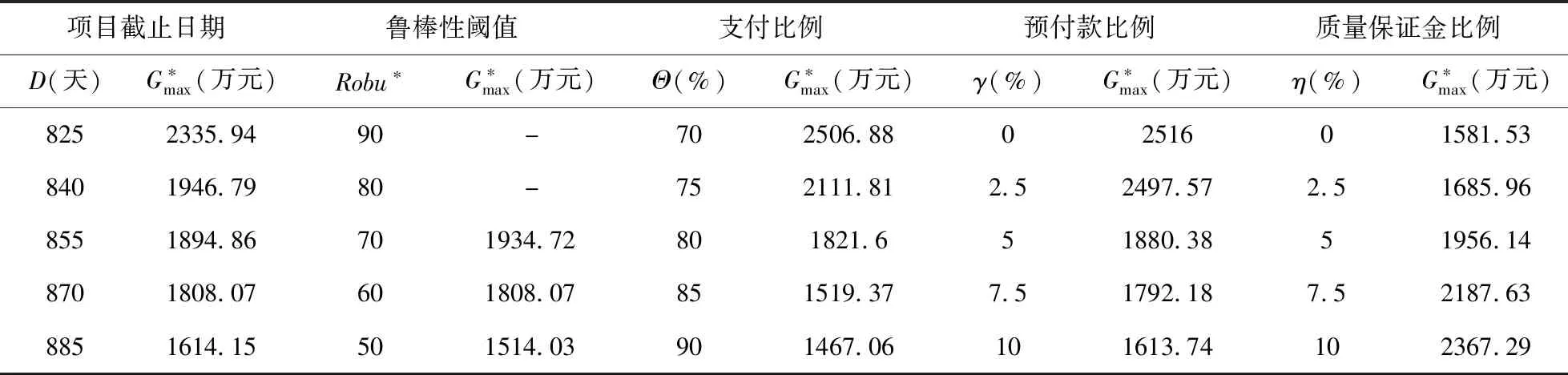
表3 承包商最大累计资金缺口随参数的变化情况

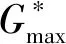
5 结论

本文采用基于活动的研究方法，研究了多模式下具有随机活动工期的现金流均衡项目调度问题。首先，界定研究问题，在截止日期约束下，安排活动执行模式与开始时间，给相关活动留有适当时间缓冲，使之满足鲁棒性阈值约束，保证基准进度的稳定性，并使得承包商在项目执行过程中的最大累计资金缺口最小；随后，在此基础上构建0-1整数规划模型，并设计模拟退火算法进行求解；最后，通过一个实例对研究问题进行说明，得到承包商现金流均衡的满意进度安排，将其与净现值最大化进度安排进行对比分析，说明本文问题模型的有效性，并讨论关键参数对现金流均衡的影响。得到结论：承包商现金流均衡情况随着鲁棒性阈值的减小而好转，且当鲁棒性阈值水平设置得过高时，问题无解。需要指出的是，在现实中，项目具有多种支付方式，将本文研究问题与支付进度问题相结合，是有待于进一步研究的问题。