基于改进FMECA方法气吸鸭嘴滚筒式排种器的可靠性分析
2019-10-24张恒康建明张国海杜洪恿蒋平彭强吉
张恒,康建明,张国海,杜洪恿,蒋平,彭强吉
(1山东理工大学农业工程与食品科学学院,山东 淄博 255000;2山东省农业机械科学研究院,山东 济南 250100)
气吸鸭嘴滚筒式排种器是播种机的重要工作部件,其可靠性程度直接影响着整机的工作性能。目前排种器的故障率依然很高,一旦发生故障,会大大降低播种质量,甚至延误农时和严重影响农民的收益,因此,对排种器进行可靠性分析十分必要。
FMECA (Failure modes,effect and criticality analysis)主要包括故障模式及影响分析(FMEA)和危害性分析(CA)两部分[1],常用于发现和解决装备系统中已知或潜在的各种故障,对提高装备的可靠性和使用寿命起到了至关重要的作用[2]。采用传统FMECA方法对装备进行可靠性分析时存在以下问题:主观性太强,确定危害等级排序时只能定性分析而无法进行定量分析,无法计算出客观的结果难以准确找出系统的薄弱环节,不能给各种装备系统的日常维修提供技术支持[3-5]。针对这些问题,国内外许多专家学者将模糊理论法引入到传统FMECA方法中,并取得了相关研究成果。有专家学者提出新的故障分析评价模型和专家评价系统,其中BRAGLIA M等[6]提出一种针对面粉加工工艺装置故障分析的评价模型,使得该装置的故障率大大降低;LEE Y S等[7]提出一种可以及时发现并处理系统高风险故障的模糊专家评价系统,大大提高了系统的安全可靠性;ZAFIROPOULOS E P等[8]提出一种针对电子产品的模糊逻辑法,对实现电子产品长期可靠运行方面起到至关重要的作用;BOWLES J B等[9]提出一种基于模糊数学计算的可靠性评价方法,在可靠性分析方面实现了故障定量化分析,结果更加准确可靠。另外,有专家学者利用改进FMECA方法对各种装备系统的可靠性进行分析,其中安颖等[10]针对CVT系统易出现的故障,采用改进FMECA方法对其进行分析,降低了故障的发生率;胡启国等[11]利用改进FMECA方法对装甲车液压系统的可靠性进行研究,解决了采用传统FMECA方法评价结果不准确的问题;夏震宇等[12]针对兵器装备易出现的各种故障,采用改进FMECA方法定量地对其进行评估,得到了准确可靠的评估结果;谭壮等[13]针对数控加工机床的加工工艺易出现的故障,率先提出应用改进FMECA方法对其进行风险评估,准确地得出了加工工艺风险等级排序。
为了提高排种器的可靠性水平,本文借鉴FMECA方法在各种装备系统可靠性分析方面的研究成果,以气吸鸭嘴滚筒式排种器为研究对象,进行基于改进FMECA方法的气吸鸭嘴滚筒式排种器的可靠性分析,得出排种器可靠性改进的重点,为排种器的后期改进设计和日常维护维修提供一定的理论指导。
1 改进FMECA方法基本理论
改进FMECA方法是在传统FMECA方法的基础上引入模糊理论法而形成的一种分析装备系统可靠性的方法,该方法融合了2种可靠性分析方法的优点,可以有效弥补传统FMECA方法存在的缺点,量化分析结果,使各故障模式的综合危害等级排序更加准确可靠,改进FMECA方法的基本评价流程[14]如图1所示。
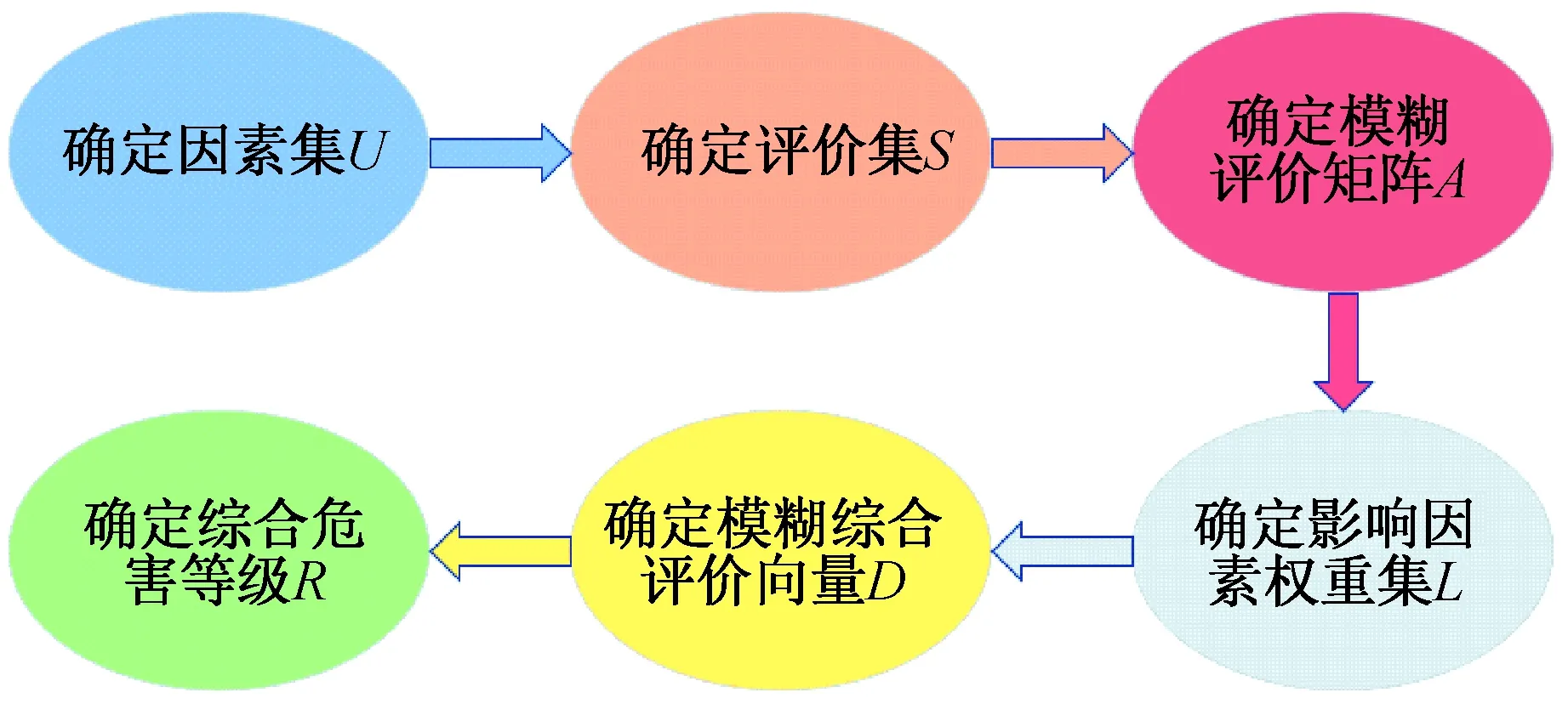
图1 改进FMECA方法的基本评价流程Fig.1 Improve the basic evaluation process of FMECA方法
1.1 确定因素集
因素集是指对评价对象产生影响的各种因素的集合,通常用U表示,即
U={u1,u2,u3,…,ui,…,um},
(1)
其中,ui表示第i个影响因素,i=1,2,3,…,m。
1.2 确定评价集
评价集是指评判专家对所评价对象做出的所有评价结果,用S表示,即
S={s1,s2,s3,…,sj,…,sn},
(2)
其中,sj表示评判专家做出的第j个评价结果,j=1,2,3,…,m。
1.3 确定模糊评价矩阵
为了确定评价结果与影响因素的关系,需要建立一个U→S的模糊映射f,使得f:U→F(S),ui→f(ui),可以得到影响因素ui相对于评价结果sj的隶属度aij,即
f(ui)=Ai=(ai1,ai2,ai3,…,aij,…,ain),
(3)
式(3)中,Ai为第i个影响因素ui的单因素评价集合。
将所有的单因素评价集合作为评价矩阵的行并进行转置,可以得到一个m行n列的矩阵,即为影响因素模糊评价矩阵,用A表示,即
(4)
邀请r位专家成立评价小组,每位专家都需要对各个影响因素ui做出相应的评价结果sj,如果r位专家中评定ui隶属于sj的有rij人,则得到ui的评价集为

(5)
1.4 确定影响因素权重集
不同影响因素对于各故障模式的危害程度存在很大差别,因此,在进行专家综合评价前,首先要根据各影响因素产生的危害程度进行排序,并按一定的顺序确定相应的权数,最后由这些权数组成影响因素的权重集合,影响因素权重集用L表示,即
L={l1,l2,l3,…,li,…,ln},
(6)
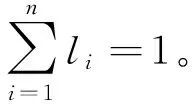
确定影响因素权重集的方法有很多,主要包括调查统计法、专家打分法以及层次分析法(AHP)[15],其中,调查统计法通过实际调研统计,分析大量数据从而得到确定的权重,但这种方法耗费大量的人力物力且周期太长而不宜采用;专家打分法通过组织专家确定权重,这种方法虽然省时省力周期短,但主观性太强,极易出现误差,不易得到理想确切的权重;层次分析法能很好弥补专家打分法的不足,去除在确定权重过程中出现的人为因素,从而得到客观、有效的权重。因此,本研究采用层次分析法1—9的标度模式确定影响因素权重集,具体步骤如下:
(1)用bij表示影响因素ui和uj的相对重要性,并组成判断矩阵B,即
(7)
其中bi的取值参考表1。显然bii=1,bij=1/bji。

表1 层次分析法影响因素相对重要程度标度值Tab.1 AHP analysis of the relative importance degree of the influencing factors
(2)通过计算一致性比率KC的数值来对判断矩阵B进行一致性检验。首先,计算判断矩阵B对应的最大特征根λmax和一致性指标IC,即
(8)
然后确定IT的数值,IT表示判断矩阵的平均随机一致性指标,可通过表2得到1~13阶判断矩阵的IT的数值。

表2 1—13阶判断矩阵的IT值Tab.2 Values 1—13 of IT judgment matrix
根据IC和IT的数值,计算一致性比率KC,即
(9)
当KC<0.1时,认为判断矩阵B的一致性满足要求,否则需要对判断矩阵B进行适当的修正。
1.5 确定模糊综合评价向量
将前面确定的影响因素模糊评价矩阵A和影响因素权重集L进行相乘,可以得到模糊综合评价向量,用D表示,即
(10)
1.6 确定综合危害等级
为了更准确地比较各故障模式对评价对象的综合危害度,需要对模糊综合评价向量D进行加权平均处理后得到具体数值,然后将各故障模式对评价对象的综合危害程度进行排序。这个数值用R表示,即
R=D·ST。
(11)
式(11)中,S表示评价结果矩阵。
2 实例应用及分析
在农业生产过程中,播种质量的好坏是作物能否实现高产的关键因素,而排种器的性能及可靠性直接影响着播种的质量,因此,对排种器进行可靠性分析十分必要。本文以气吸鸭嘴滚筒式排种器为例,对此类型的排种器进行可靠性分析。
2.1 气吸鸭嘴滚筒式排种器
气吸鸭嘴滚筒式排种器结构如图2所示,主要包括鸭嘴组件、导种盘、刷种装置、吸种盘、刮种器、排种器端盖、排种器穴播盘等。

1—鸭嘴组件;2—导种;3—刷种装置;4—吸种盘;5—刮种器;6—排种器端盖;7—排种器穴播盘。图2 气吸鸭嘴滚筒式排种器结构图Fig.2 Structure of the air suction duckbill drum type metering device
排种器工作时,种子通过导种盘进入排种器内部,吸种盘在风机作用下产生负压气室,随着吸种盘的旋转,种子不断被吸附到吸种盘开口处,在刷种装置作用下根据播种要求将多余的种子刮掉;当吸种盘吸附的种子到达落种区时,断气片暂时封闭吸种口,使得负压消失,并在刮种器作用下将种子脱离吸种盘;随后在种子自重、刮种器推力及排种器离心力综合作用下进入导种槽内,当鸭嘴组件竖直入土最深时鸭嘴开启并打出孔穴,种子依靠自身重力落入孔穴中,即完成整个播种过程。
2.2 气吸鸭嘴滚筒式排种器FMEA方法分析
对气吸鸭嘴滚筒式排种器的故障模式进行全面分析,结果见表3。

表3 气吸鸭嘴滚筒式排种器FMEA方法分析表Tab.3 Air suction duckbill drum type metering device FMEA method analysis table
2.3 气吸鸭嘴滚筒式排种器改进FMECA方法分析
为了定量分析FMEA的分析结果,采用改进FMECA方法对气吸鸭嘴滚筒式排种器进行可靠性分析,得到更准确的各故障模式危害等级排序,从而采取适当的处置措施,及时排除故障,保证气吸鸭嘴滚筒式排种器高效可靠的工作。在对气吸鸭嘴滚筒式排种器进行FMEA方法分析的前提下,对其常见故障模式分别进行模糊综合评判,具体步骤如下所示:
(1)确定因素集合。
在对气吸鸭嘴滚筒式排种器进行故障危害等级评判时采用下面的因素集合,即U={故障发生概率(u1),故障影响程度(u2),故障发现难易程度(u3),故障排除难易程度(u4)}。
(2)确定评价集合。
对于各个影响因素的评价来说,没有绝对的“好”和绝对的“差”,因此,在两极限之间增加“较好、较差”2个等级,设置影响因素评价等级数为4,即S={1,2,3,4}。各影响因素的评价等级如表4所示。

表4 各影响因素评价等级表Tab.4 Rating scale of each influencing factor
(3)确定模糊评价矩阵。设经过专家组的评定,空穴率过大故障发生概率模糊集合为a1={0,0.3,0.6,0.1},故障影响程度模糊集合为a2={0,0.3,0.5,0.2},故障发现难易程度模糊集合为a3={0.7,0.2,0.1,0},故障排除难易程度模糊集合为a4={0.5,0.3,0.1,0.1},由此可以得到空穴率过大故障的模糊评价矩阵为
(12)
(4)确定空穴率过大的影响因素权重集。根据空穴率过大故障影响因素的评判结果,构成各影响因素判断矩阵,并通过相应的计算得到其权重值,如表5所示。
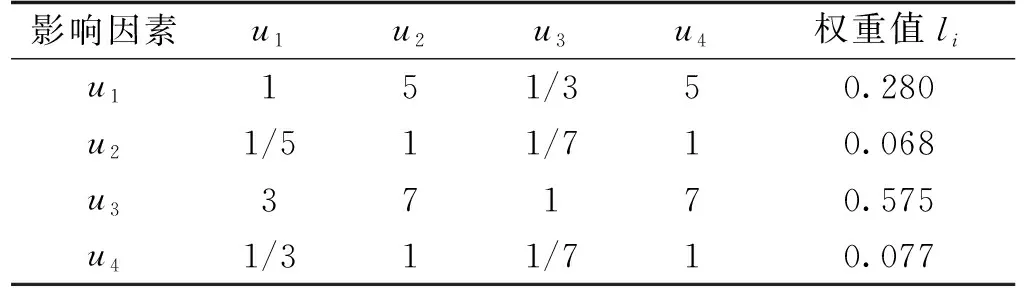
表5 空穴率过大各影响因素判断矩阵及权重值Tab.5 Judgment matrix and weight value of each influencing factor of the plugging device
由表5可以得出判断矩阵为

(13)
根据一致性比率KC的数值对判断矩阵B进行一致性检验。由矩阵B计算出其对应的最大特征根λmax=4.13,代入式(8)可得一致性指标IC=0.043;由表2可得IT=0.90,将数据代入式(9)可得KC=0.048<0.1,表明判断矩阵B的一致性满足要求。据此可以得到空穴率过大故障对应的因素权重集为
L1={0.280,0.068,0.575,0.077}。
(14)
(5)对空穴率过大故障进行模糊综合评判。
根据式(10)可得故障模式1的模糊综合评价向量为D1=L1·A1=[0.3604 0.2381 0.2962 0.1053],说明空穴率过大故障对危害度等级1、2、3、4的隶属度分别为0.4410、0.2425、0.2672、0.0493。
(6)确定空穴率过大故障的综合危害度等级R1。
根据式(11)可以求得
R1=D1·[1,2,3,4]T=2.1464。
(15)
(7)同理确定故障模式2至6的模糊评价矩阵分别为
因故障模式1—6的各影响因素判断矩阵相同,故可采用相同的因素权重集进行计算,即L1=L2=L3=L4=L5=L6。根据式(10)可得各故障模式的模糊综合评价向量为
D2=L2·A2=[0.4256,0.2154,0.2469,0.1121],
D3=L3·A3=[0.4410,0.2425,0.2672,0.0493],
D4=L4·A4=[0.3029,0.1729,0.4401,0.0841],
D5=L5·A5=[0.5139,0.1976,0.2460,0.0425],
D6=L6·A6=[0.4831,0.1724,0.3020,0.0425]。根据式(11)可以求得空穴率过大故障的综合危害等级为:
R2=D2·[1,2,3,4]T=2.0455,
R3=D3·[1,2,3,4]T=1.9248,
R4=D4·[1,2,3,4]T=2.3054,
R5=D5·[1,2,3,4]T=1.8171,
R6=D6·[1,2,3,4]T=1.9039。
再根据计算出的各故障综合危害等级数值,6个故障模式的危害度等级从大到小依次为:故障模式4>故障模式1>故障模式2>故障模式3>故障模式6>故障模式5。
利用该方法同样可以对其他农业装备进行可靠性分析,找到危害性最大的潜在故障,及时采取措施消除故障并对其改进设计,从而提高农业装备的可靠性。
3 结论
(1)本文将传统FMECA方法与模糊理论法相结合,建立了基于改进FMECA方法的可靠性分析方法,通过该方法能准确得出气吸鸭嘴滚筒式排种器的薄弱环节,可为各种农业装备可靠性提供技术支持,并为其他类型装备系统的可靠性分析提供借鉴。
(2)故障模式4的危害性最大,是可靠性改进的重点,故障模式1的危害性次之。这可以为排种器后期改进设计提供理论依据,并能对排种器可能出现的故障进行事前检查,从而降低排种器的故障发生率,提高气吸鸭嘴滚筒式排种器的可靠性水平。
