基于Dijkstra算法的铁路应急物资调配方案研究

王华梅，王 璞，刘兴奇

（1.太原铁路局集团有限公司，太原 030013；2.中国铁道科学研究院集团有限公司，北京 100081；3.成都铁路局集团有限公司，成都 610081）

随着铁路的高速发展，铁路安全问题越来越受到学者的密切关注。由于铁路应急物资来源分散，若几个应急点同时发生事故，应急优先级又存在区别，铁路应急物资调配工作则会面临严峻考验[1]。胡耀民，刘春年[2-3]等人在突发事件响应过程中根据铁路应急物资需求，提出应急物流快速响应调配策略。李聪[4]等人通过使用排队论GI/M/1模型，推导出应急救灾车辆的平均等待时间和队长的表达式，为物资装载服务台的数量增减问题和应急救灾车辆等决策提供依据。徐翠翠[5]分析了应急物资管理系统和应急物资管理信息系统的构建及其中涉及的布局问题。曾敏刚等人[6]在可以准确地获取各需求点受灾数据的前提下，集成研究灾后应急服务设施中心选址和运输路径选择问题，建立以设施点建设成本、运输成本和灾害损失成本之和最小为目标的LRP模型。

现有文献主要关注的是应急物流响应、应急车辆调度和配送路径等方面的问题。借助现有研究基础，旨在从铁路应急物资调配环节的特殊性出发，基于Dijkstra（狄克斯特拉）算法，在从储备点到应急点的最优路径决策中，以最短时间和最小损失为根本目标，依据应急点的不同紧急程度，建立铁路应急物资调配方案，以其通过充分利用有限资源，提高应急管理效率。

1 铁路应急物资调配方案建立

1.1 Dijkstra算法概述

最优路径选择问题[7]属于运筹学理论的一部分，实质是在固定起始点的条件下，得出两个或多个已知点间的最优路径选择。路径优劣的评价指标可用长短、时间、费用等方式表示，基于应急物资的特殊性，本文将选取时间作为评价指标。由求解每项活动的最早发生时间和最晚发生时间而确定最优路径， 若一项活动的最早发生时间和最晚发生时间相同，说明该活动是关键活动，所经过的路径即是所要求解的最优路径。假设图G，V为图G中的某一点，E为图G中各点的边。其最优路径的数学表示如下：

若图G中的边是有权的，设W(e)≥0为连接两个点Pi、Pj的线u(Pi,Pj)的权值，定义W(u)为路径u的长度。路径u(Pi,Pj)的最小值就是其最短路径，为：

Dijkstra算法主要思路为：设G=G(V,E)是赋权有向图，将顶点集合分成两组，一组是已求出的到达源点的最短路径的集合（初始只包含源点）称为已优化路径集合，用集合S表示；另一组是还未求出的到达源点的最短路径的集合，称为未优化路径集合，用集合U表示。开始求取最短路径时，目标是从起始点出发到达目标点的路径上的顶点。计算过程中，每得到一个最短路径就把源点通过该路径连接的顶点加到集合S中，将集合U中的顶点加到集合S的过程中，应按最短路径长度的递增次序依次添加，并且要始终确保源点到集合S中任意顶点的距离都要≤源点与集合U中任意顶点的距离。该算法就是按照上述步骤，将集合U中的点全部加入到集合S中，直至集合U中没有点，完成一个计算循环。值得注意的是Dijkstra（狄克斯特拉）算法只适用于W(e)≥0的情形，当赋权有向图中存在负权时，则算法失效。如图1所示的赋权有向图中，如果用Dijkstra（狄克斯特拉）算法，可得出v1到v2最短路的权是1，但这显然是不对的，因为从v1到v2的最短路是（v1，v3，v2），权是 -1。

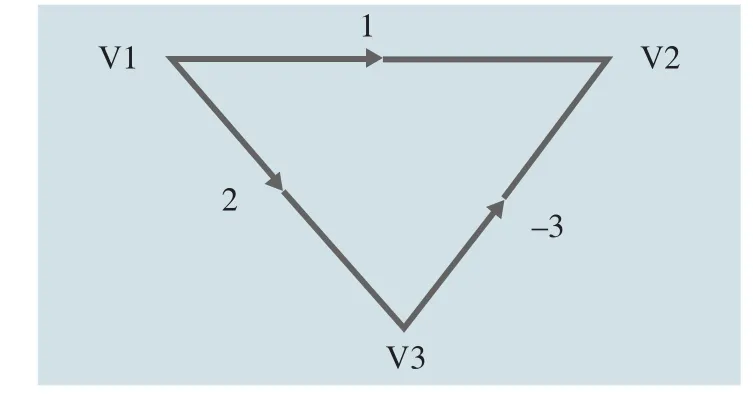
图1 赋权有向图

在计算从v到k的最短路径的过程时，潘开灵等人采用以下步骤[9]：

设图G=G(V,E,W)中有n个顶点，W(u)是从源点到每个终点的当前最短路径u的长度，集合S包含所有已求出的到达v最短路径的点。集合U为V-S，在起始状态下包含除源点外的所有点。

（1）根据距离最小原则找到U中到源点v距离最小的一个点，设为k，并将k放入S中。

（2）将步骤（1）中顶点k作为新参照点，再将U中所有点通过k到达v的距离与不通过k到达v的距离对比，若前者小于后者，这个点的距离要修改为k到达v的距离和上一个顶点到这个k的距离之和。

（3）重复上述步骤，直到U中的所有点都被放入S中时结束。

本文基于Dijkstra算法，从铁路应急物资量和应急物资调配时间两个维度，建立铁路应急物资调配方案。

1.2 铁路应急物资量

铁路应急救援工作主要关注的问题：（1）高效开展抢险救援工作；（2）全力减少各方面损失。

有序开展铁路应急物资的调配工作是铁路系统恢复运行的关键，而确定应急物资的供需量则是开展物资调配工作的前提[8]。因此首先分析铁路应急物资的储存量和需求量。

当一个区域发生突发事件，需要开展应急响应工作时，要考虑的即为该区域内应急物资储备点和突发事件应急点的个数。要及时掌握每个储备点的各类物资储存量，并对每个应急点的物资需求量进行合理预推，为高效率开展应急工作奠定基础。假设：铁路网络的某一部分含有S1，S2，…，Sn，共n个物资储备点；D1,D2,…,Dm，共m个应急点，Si与Dj之间通过路径rij连接。Si内含有xik个Tk种类的物资，铁路应急指挥中心预测每个应急点Dj需求物资Tk的量是yjk。本文同时考虑到储备点储存量和应急点需求量两个要素，确定科学合理的铁路应急物资调配方案。

1.3 铁路应急物资调配时间

在任何行业或情况的应急物资调配工作中，时间都是决策者考虑的问题，关键是如何迅速地将各类应急物资调配到突发事件应急点。所以，在应急响应工作中，需要通过确定最优路径来将应急物资及时送达各应急点。

1.4 铁路应急物资调配方案的确定

由于铁路应急物资有限的储存量这一约束条件存在，在确定铁路应急物资调配方案时，要确保优先救援优先级较高的突发事件应急点和选择最优配送路径。同时，还要兼顾各类铁路应急物资的储存量能否满足应急需求[9]。假设某线路发生突发事件，需要调配物资进行抢险，该区域内有S={Si|i=1，2，…，n}共n个物资储备点，有D={Dj|j=1，2，…，m}共m个应急点，每个储备点内有T={Tk|k=1，2，…，q}共q种物资。

为建立应急物资调配方案，给出以下说明：

(1)应急点j对物资h的需求量为物资可以从应急点j周边的储备点获得，如式（3）所示。

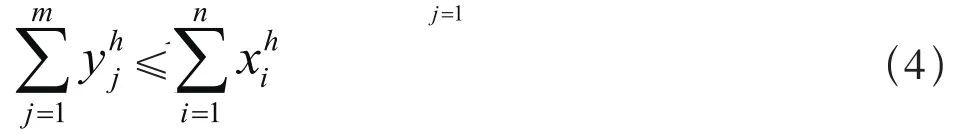
(3)当储备点i内储备的物资h无法全部满足多个应急点的需求时，首先满足优先级或重要度高的应急点的需求，优先级或重要度较低的应急点对物资h的需求可以从配送时间较长的其他铁路应急物资储备点满足。

(4)当应急物资需求点j对物资h在其最佳供应点无法全部得到满足时，剩余部分从其次优物资储备点进行调配。

2 算例分析

2.1 应急物资调配路径

本文应用MATLAB软件进行仿真求解。假设突发事件应急点就近范围内有两个应急物资储备点，分别用红色圆圈1和2表示；在该区域中有3个应急点，分别用绿色圆圈12、13和14表示。将每个储备点和应急点都放在图中，建立一个交通网络系统，铁路应急物资调配交通网络图，如图2所示。

对图2的储备点和应急点进行节点编号，具体编号，如表1所示。

同时，结合当地道路信息估算推测应急物资配送过程中通过每段路径所需要的时间结算结果，如表2所示。

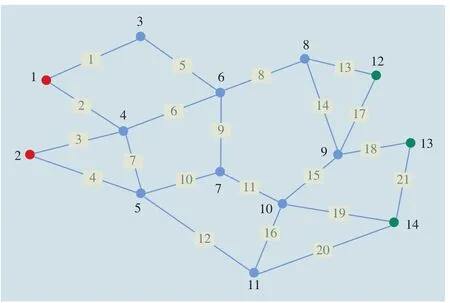
图2 该区域铁路交通网络图

表1 应急点编号表

突发事件发生后，根据Dijkstra最优路径决策方法，可以求得各物资储备点到各应急点的最优路径，如表3所示。

通过表3，可以清楚的看出每个储备点到每个应急点的路径编号，迅速的确定最优调配路径。

2.2 应急物资调配方案确定

铁路系统中的设备设施种类繁多，在突发事件发生时，各个应急点对应急物资的需求种类和数量也存在多样性。在建立铁路应急物资调配方案时，必须考虑各类物资的需求量和供应量，将二者结合在一起进行综合分析。由于不同应急点紧急程度不同，在此假设应急点调配物资优先级为D2>D1>D3，即优先配送D2，然后配送D1，D3。在突发事件发生时，铁路局可以通过物资部门或信息系统获取各储备点的各类应急物资储备量信息，如表4所示。

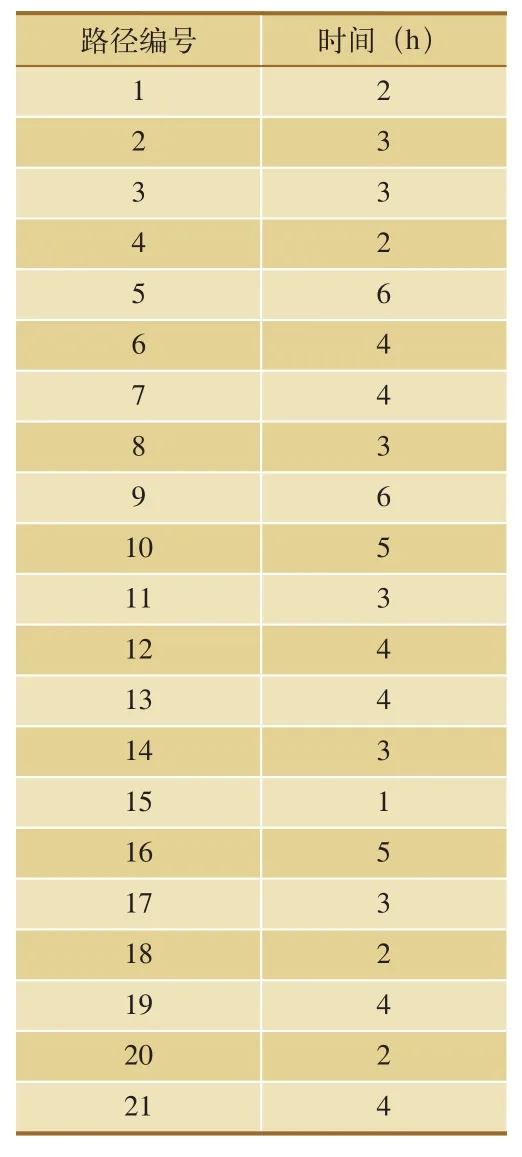
表2 应急物资运输时间估算表

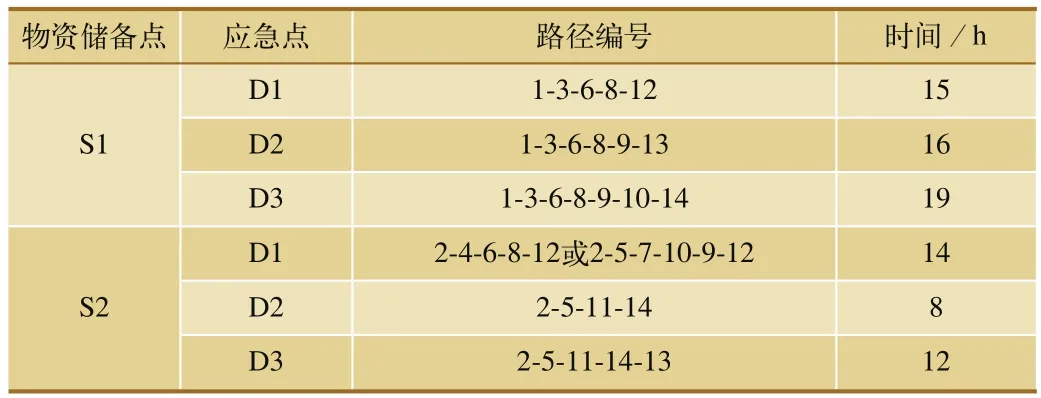
表3 储备点到各应急点的路径编号及所用时间

表4 储备点的各类物资储存量 单位：个

根据历史经验和现场实际情况，应急指挥中心可以对每个应急点的各类应急物资需求量做出预估，如表5所示。

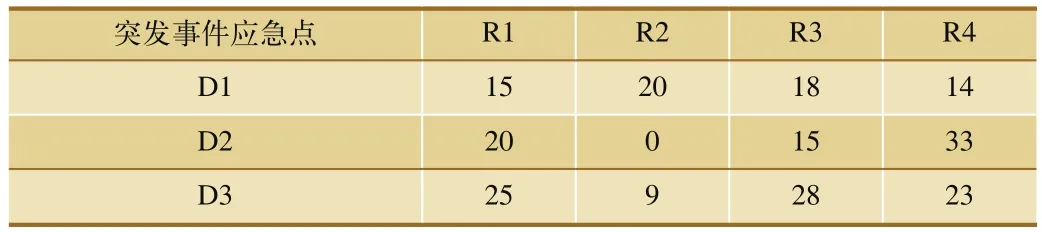
表5 应急点的各类物资需求量 单位：个

根据应急物资调配方案，对上述应急物资进行合理分配，最后得到一个包含应急物资储备点到应急点间的最优路径、各类物资需求量和供给量及调配方案的综合铁路应急物资调配方案表，如表6所示。

表6 突发事件应急物资调配方案表

从表6中可以看出突发事件发生后各应急点的各类应急物资需求情况以及运输路径选择方案，综合确定调配应急物资的储备点、选择合理的配送路线、确定各类物资数量的供给情况，从而可以迅速开展铁路应急物资调配工作。

通过对铁路应急点的分析，开展一次实际的铁路应急物资调配方案建立工作，验证本文提出的调配方案。本次验证可得到每个应急点调取需求物资的储备点，并且确定相应的最优运输路径方案。值得注意的是，在匹配应急点和供给点时，要考虑供给点的物资储备量能否完全满足应急点对各类物资的需求。

3 结束语

对于铁路应急物资调配问题，以最优应急物资配送路径和确保优先救援优先级或重要度较高的应急点为前提，兼顾各类应急物资储备点的供给能力和各应急点的需求状况，通过Dijkstra（狄克斯特拉）算法确定调配最优路径，从而确定整体应急物资调配方案。本文假设物资需求可以完全得到保障，不存在供给无法满足需求的情况。没有充分考虑铁路应急储备点物资供应量无法满足所有事故灾害点物资需求量的情况，后续研究可以考虑供应量不足时的调配方案问题。

最后通过算例分析，表明这种算法和方案是有效的，并且对最大限度地发挥资源的效益及保证铁路安全和社会稳定有一定价值和意义。