螺栓法兰接头用碟形弹簧压缩回弹性能研究*

(南京工业大学机械与动力工程学院 江苏南京 211800)

螺栓法兰接头在压力容器及管道连接上被广泛应用，而泄漏则是螺栓法兰连接主要的失效模式。高、低温或变工况条件下，螺栓法兰接头各元件会发生不同程度的变形，导致垫片工作密封应力不足，发生泄漏。而碟形弹簧是一种刚度大、具有变刚度特性、轴向尺寸较小，且能在发生小变形时承受较大载荷的弹性补偿元件[1]。在螺栓法兰接头中加装碟形弹簧，当螺栓预紧时，碟簧处于压缩状态，吸收机械能转化为弹性势能，当螺栓法兰接头长期在高温高压、温度及压力波动、机械振动下工作导致螺栓预紧力不足时，碟簧将储存的弹性势能转化为机械能，补偿垫片及螺栓的变形量，保证螺栓预紧力满足密封要求。

GB/T 1972-2005[2]给出了碟簧的标准尺寸和设计计算方法，其设计方法为ALMEN-LASZLO[3]近似解法(简称A-L法)，该方法忽略了径向应力及接触表面的摩擦力，假设材料为完全弹性不发生塑性变形，该标准规定碟簧最大服役载荷为压平位移的75%所对应的载荷。CURTI等[4]在A-L解的基础上对假设条件进行改进而提出一种计算方法(简称C-O-P法)，但该方法沿用了A-L的推导方法。邱梅开[5]假设仅由弯曲力一项引起的径向应力为0，由薄膜力一项引起的径向应变为0，得到了较A-L法、C-O-P法更精确的计算公式。易先忠[6-8]从厚板变形理论和板壳理论出发，得到了精度高、适应范围广的解析解。张育等人[9-10]通过有限元计算对碟簧的压缩回弹性能及设计方法进行了研究，但其仍然参照了国标中的计算公式。用于螺栓法兰接头的碟形弹簧要求在螺栓预紧力下达到完全压平，其承载力要求较大、变形机制较为复杂，若仍然沿用A-L设计方法，将导致设计出的碟形弹簧承载力低，无法起到充分的弹性补偿作用[11-15]。因此，亟需开展螺栓法兰接头用碟形弹簧力学性能表征模型的研究。

本文作者通过有限元软件ABAQUS模拟分析了螺栓法兰接头用碟形弹簧力学性能，研究了各结构参数对碟簧压缩回弹性能的影响，基于正交试验和量纲分析，拟合得到了碟簧压平载荷及回弹方程的预测模型，为螺栓法兰接头用碟形弹簧的设计提供了参考。

1 碟形弹簧力学性能有限元分析方法

螺栓法兰接头碟形弹簧安装情况如图1所示。如图2所示，碟簧内径d=40 mm，外内径比C=1.9，厚度t=10 mm，倾角α=3°。建立碟形弹簧力学性能分析的弹塑性有限元模型(如图3所示)，碟簧设置为可变形体，弹性模量E=205 GPa，泊松比μ=0.3，设置材料的塑性参数如表1所示，表中数据由制造碟簧用某一耐热钢经拉伸试验得到；上、下压头简化为刚体。碟簧内缘上边和外缘下边的小平面与上、下压头分别设置为面面接触，接触面间的摩擦因数设置为0.18，对下压头设置为固支，对上压头施加向下的位移载荷0.645 mm，碟簧网格采用C3D8R，网格如图4所示。

图1 碟形弹簧安装示意图Fig 1 Schematic diagram of disc spring installation

图2 碟形弹簧纵截面剖视图Fig 2 Sectional view of longitudinal section of disc spring

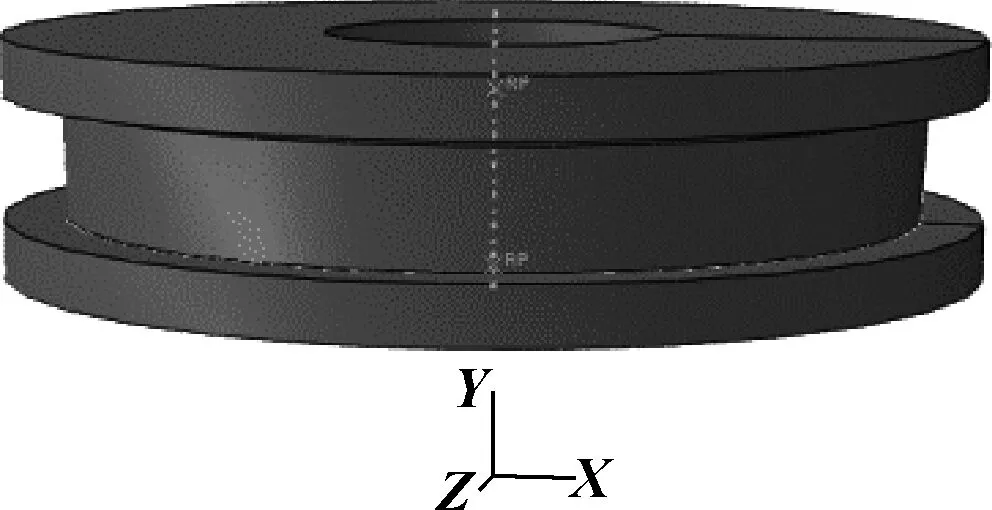
图3 三维有限元模型Fig 3 Three-dimensional finite element model表1 材料的塑性参数Table 1 Plastic parameters of materials

应变应力σ/MPa01 562.7030.009 9561 580.3410.010 3941 597.7370.012 4011 663.4700.013 5071 687.2000.014 5741 700.0160.016 1561 719.7360.018 1071 737.7100.020 6211 756.7700.022 1071 763.477

图4 三维有限单元网格图Fig 4 3D Finite element mesh diagram

2 试验验证

对与上述模拟结构尺寸相同的碟形弹簧进行压缩回弹试验，试验设备为MTS 311.32试验机，在上压头安装位移计获得精准的轴向位移数据(如图5所示)，载荷数据采用试验机输出的轴向载荷。加载方式为位移加载0.645 mm，加载速率为0.1 mm/min。

碟形弹簧的压缩回弹性能曲线如图6所示，模拟计算值与试验结果基本一致，轴向载荷最大相差6 kN，故文中模拟设置具有可靠性，可用于进一步的研究工作。

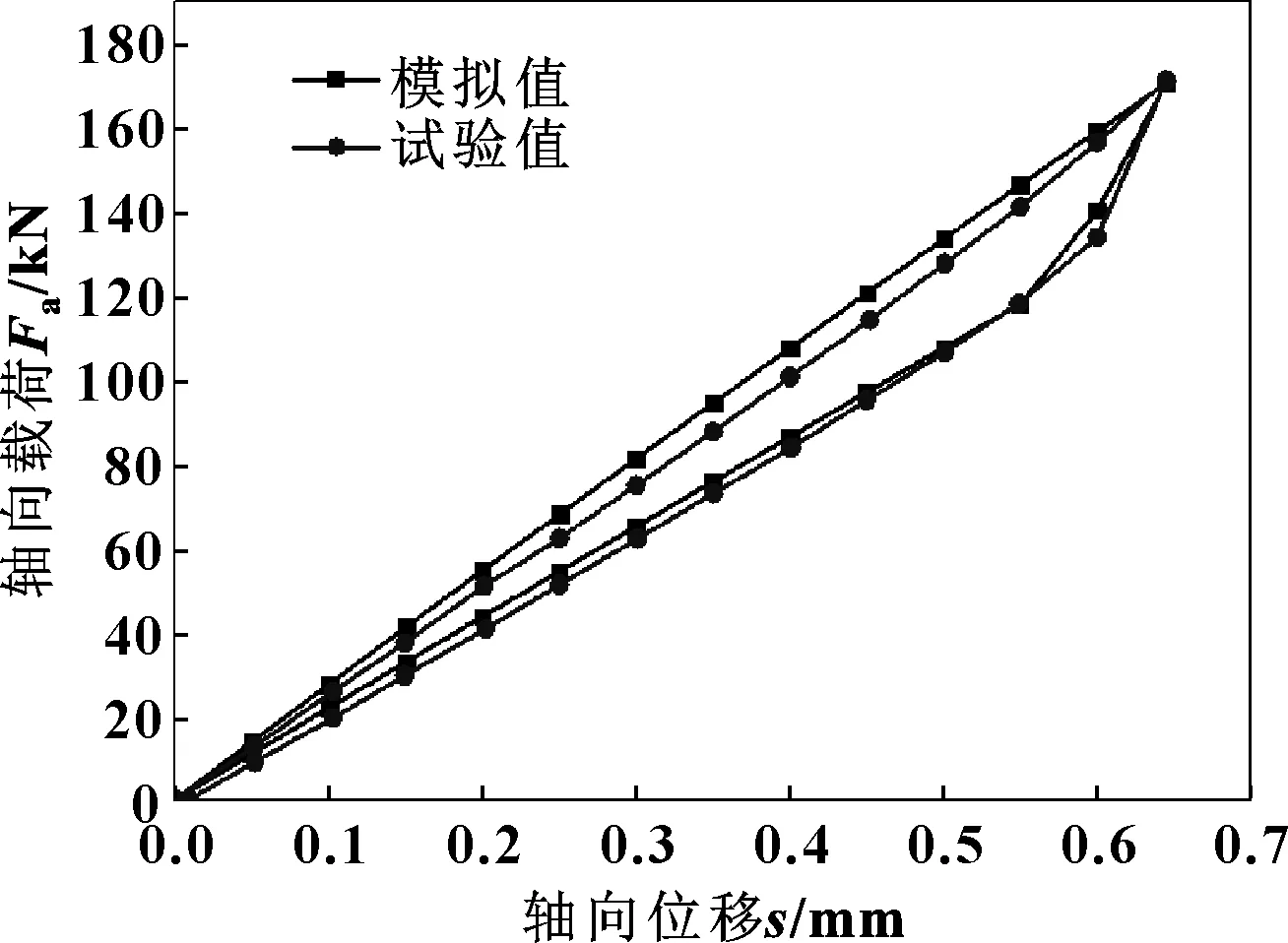
图6 碟簧压缩回弹曲线模拟与试验值对比Fig 6 Comparison of compression spring back curve and experimental value of disc spring

3 碟形弹簧结构参数对压缩回弹性能的影响

碟簧的结构参数主要有内径d、厚度t、倾角α、外内径比C。当碟形弹簧应用在螺栓法兰接头时，碟簧内径可直接根据螺栓大径(d1)确定，即d=d1+Δd(Δd为1～2 mm)。因此，文中主要研究厚度、倾角、外内径比对碟形弹簧压缩回弹性能的影响。

3.1 厚度对碟形弹簧压缩回弹性能的影响

取内径d=40 mm，外内径比C=1.9，倾角α=3°，厚度t分别为8、9、10、11和12 mm的碟形弹簧，研究碟形弹簧厚度对其压缩回弹性能的影响，结果如图7所示。当碟簧的其他结构参数水平一定时，随着厚度值的增加，碟簧自由高度基本不变，但碟簧刚度变大，因此，压平载荷呈大幅度上升。图8示出了碟簧厚度对其等效塑性应变的影响趋势，随碟簧厚度的增加等效塑性应变区域不断扩大，等效塑性应变值不断增加，因此，回弹率总体呈现下降趋势。

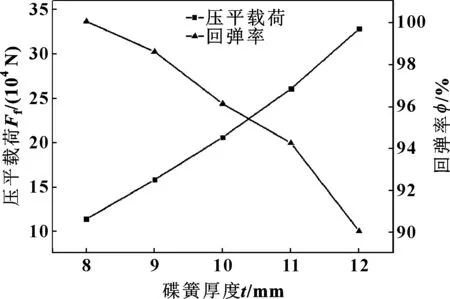
图7 碟簧厚度对其压平载荷及回弹率的影响Fig 7 Effect of the thickness of disc spring on its flattening load and rebound rate

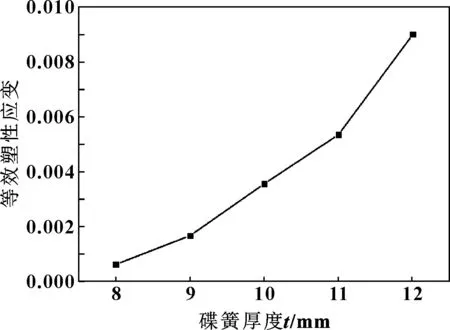
图8 碟簧厚度对其等效塑性应变的影响Fig 8 Effect of the thickness of disc spring on its equivalent plastic strain

3.2 倾角对碟形弹簧压缩回弹性能的影响

取内径d=40 mm，外内径比C=1.9，厚度t=10 mm，倾角α分别取1°、2°、3°、4°和5°的碟形弹簧，研究碟形弹簧倾角对其压缩回弹性能的影响，结果如图9所示。当碟簧的其他结构参数水平一定时，随着倾角度数的增加，碟簧自由高度大致呈倍数增加，压平载荷逐渐增大。图10示出了碟簧倾角对其等效塑性应变的影响趋势，等效塑性应变区域分布在内缘上下边，且随倾角的增大该区域不断扩大、等效塑性应变值不断增大，因此，回弹率整体呈现下降趋势。

图9 碟簧倾角对其压平载荷及回弹率的影响Fig 9 Effect of the inclination angle of disc spring on its flattening load and rebound rate

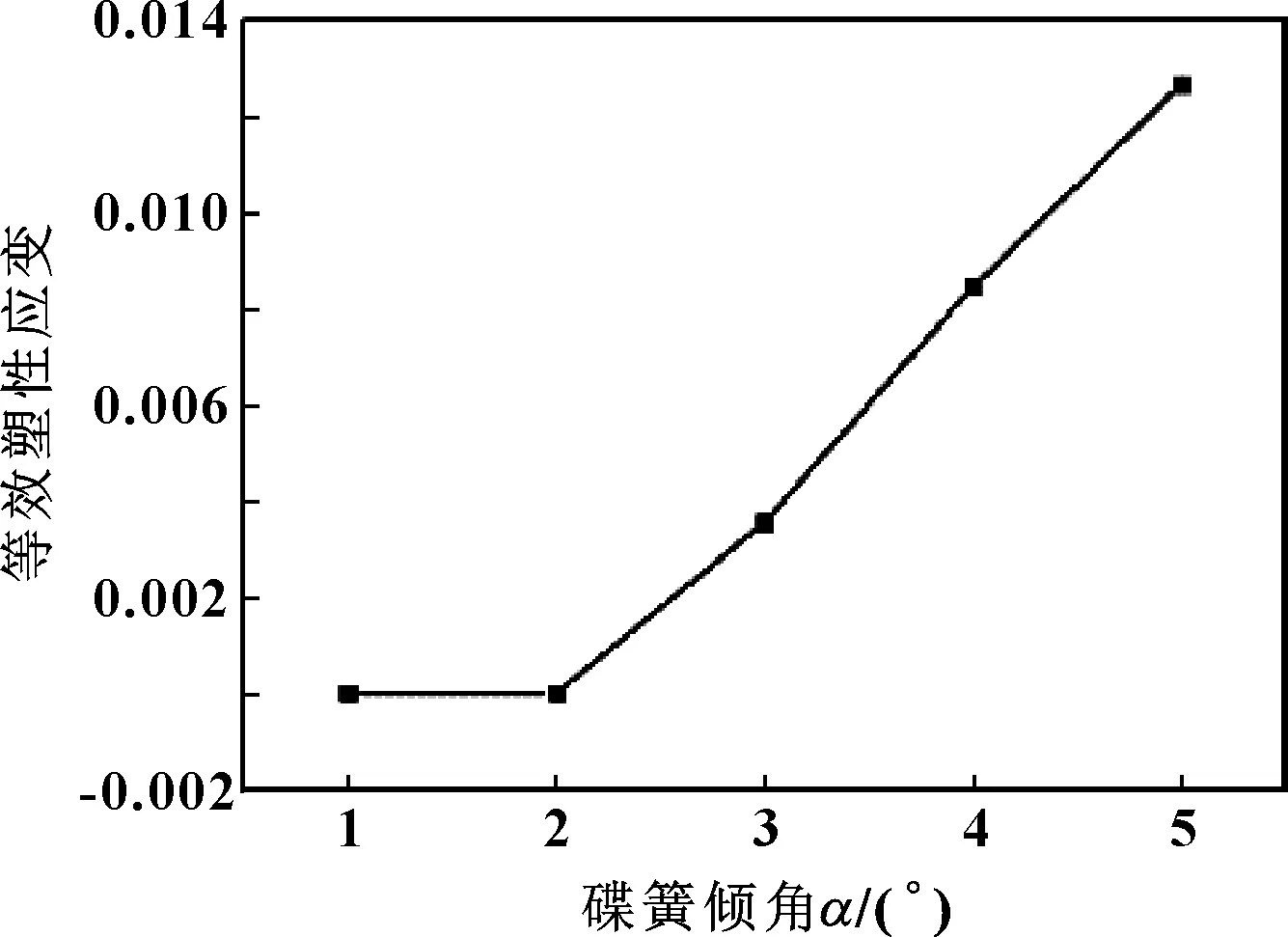
图10 碟簧倾角对其等效塑性应变的影响Fig 10 Effect of the inclination angle of disc spring on its equivalent plastic strain

3.3 外内径比对碟形弹簧压缩回弹性能的影响

取内径d=40 mm，厚度t=10 mm，倾角α=3°，外内径比C分别取1.5、1.7、1.9、2.1和2.3的碟形弹簧，研究碟形弹簧外内径比对其压缩回弹性能的影响，结果如图11所示。

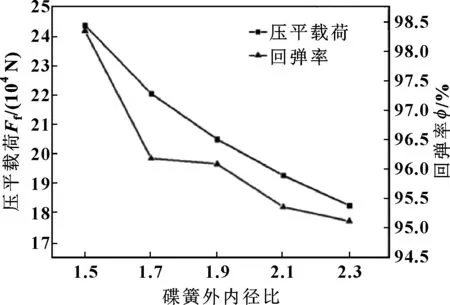
图11 碟簧外内径比对其压平载荷及回弹率的影响Fig 11 Effect of the ratio of the outer diameter to the inner diameter of disc spring on its flattening load and rebound rate

当碟簧的其他结构参数水平一定时，随着外内径比的增大，碟簧刚度减小，因此，压平载荷变小。图12示出了碟簧外内径比对其等效塑性应变的影响趋势，等效塑性应变区域集中在内缘上下边，随外内径比的增大，等效塑性应变值增大，因此，回弹率整体呈下降趋势。

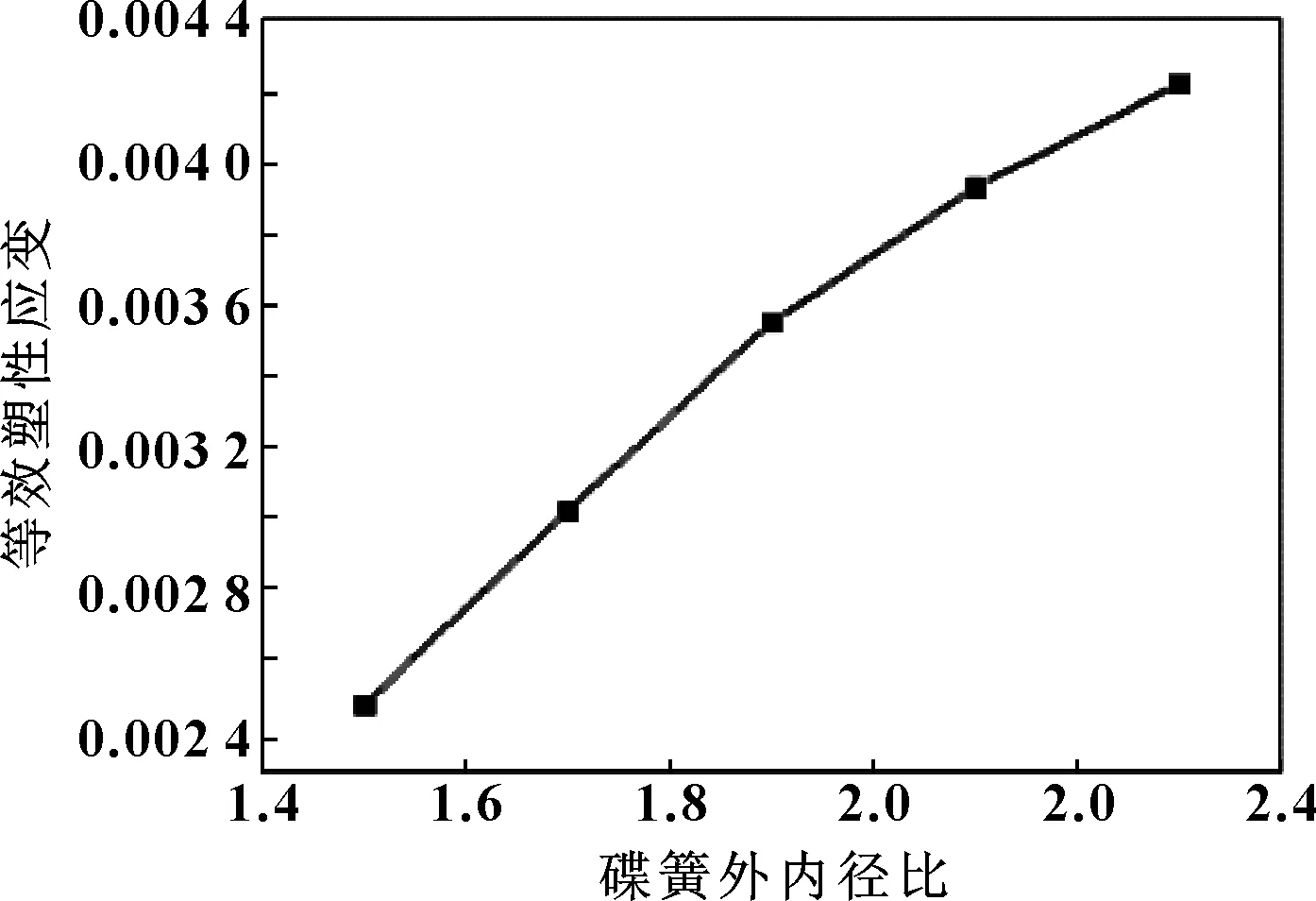
图12 碟簧外内径比对其等效塑性应变的影响Fig 12 Effect of the ratio of the outer diameter to the inner diameter of disc spring on its equivalent plastic strain

4 碟形弹簧压平载荷及回弹方程预测模型

从螺栓法兰接头用碟形弹簧的实际使用情况分析，碟簧在预紧工况下一般为压平状态，当螺栓法兰连接系统受到温度、压力波动影响造成螺栓预紧力不足时，碟簧发生回弹来补偿这部分变形量。因此，在碟簧的整个压缩回弹过程中，若已知碟簧尺寸即可得到压平载荷及回弹段载荷位移方程，可为碟簧的系列化设计及工程应用提供极大的便利。

4.1 碟形弹簧压平载荷预测模型

为得到螺栓法兰接头用碟形弹簧的压平载荷预测模型，对碟簧参数采用6因素5水平的正交试验设计，如表2所示。6因素5水平共有25个不同的碟簧尺寸，对每一个碟簧尺寸建模进行数值模拟，提取模拟结果可得各碟簧压缩回弹过程的载荷位移数据。

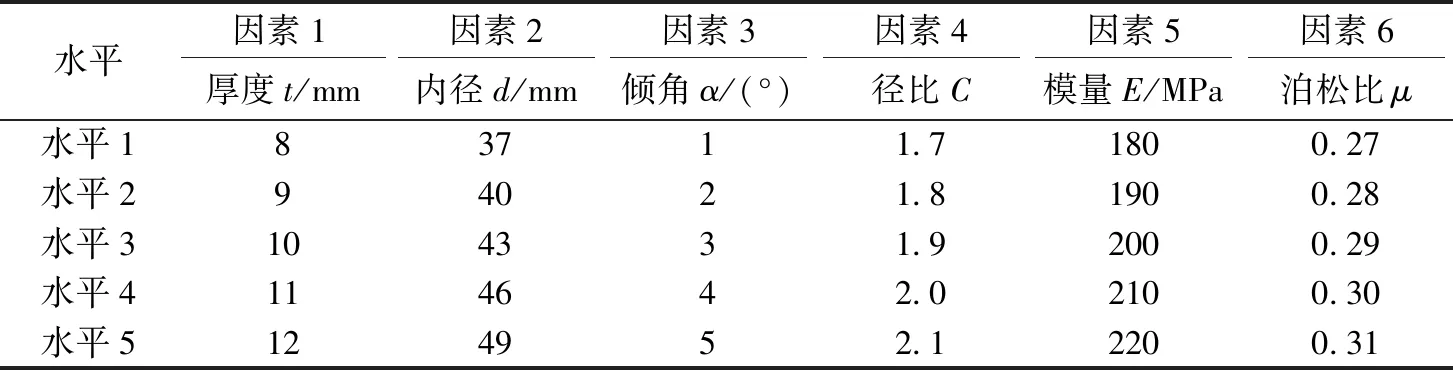
表2 因素水平表Table 2 Factor level table

对碟形弹簧的结构参数及材料参数进行量纲分析，各物理量的量纲如表3所示。可知，上述物理量涉及到长度L、质量M这2个基本量纲。由定理，选取与基本量纲数目相同的基本物理量数，故选取d、E作为基本物理量，将余下的物理量F、t、α、C、μ分别与基本物理量组成无量纲准数π1、π2、π3、π4、π5，即：

π1=da1Eb1F

(1)

π2=da2Eb2t

(2)

π3=da3Eb3α

(3)

π4=da4Eb4C

(4)

π5=da5Eb5μ

(5)

对π1而言，其量纲为

M0L0T0=La1(ML-1T-1)b1(MLT-2)

(6)

令上式成立，解得：

a1=-2，b1=1

(7)

代入得：

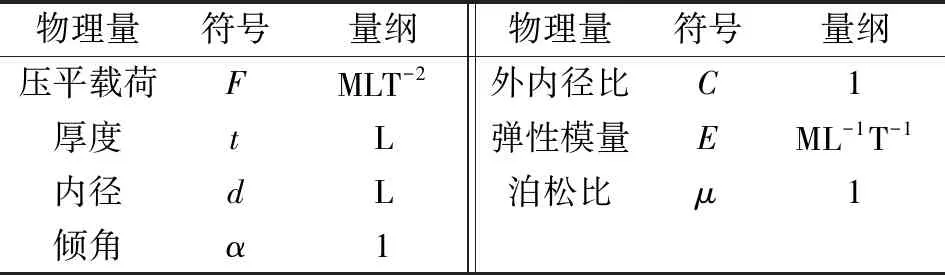
(8)表3 各物理量量纲分析Table 3 Dimensional analysis of physical quantities

按照同样的方法可以得到：

π2=t/d

(9)

π3=α

(10)

π4=C

(11)

π5=μ

(12)

相应的公式表示为

(13)

以幂函数的形式可表示为

(14)

将模型线性化，两边取对数得：

(15)

根据25组碟形弹簧载荷-位移计算结果，对公式(15)进行多元线性回归，得到公式中各参数为

lnk=6.754 4，a=2.628 4，b=0.891 4，c=-0.583 7，d=0.471 0

(16)

即得到压平载荷预测模型：

(17)

使用3个不同结构参数的碟簧对该压平载荷预测模型进行验证，碟簧具体尺寸、各组压平载荷及误差如表4所示。可知，3组碟形弹簧模型的压平载荷预测值和模拟值误差较小，说明该压平载荷预测模型是可靠的。

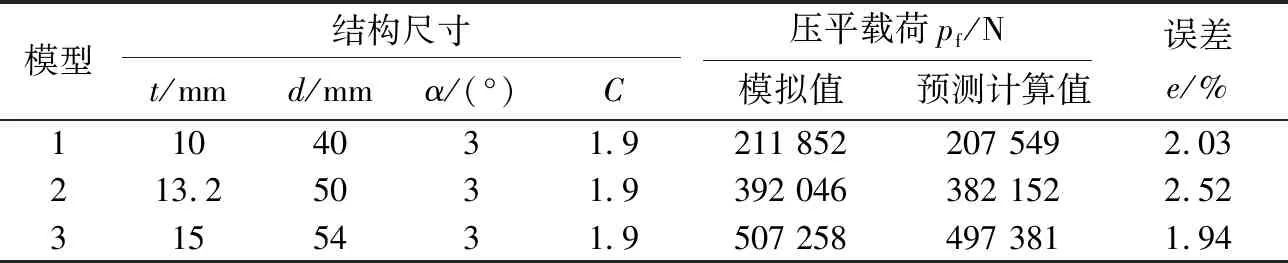
表4 碟形弹簧尺寸及压平载荷预测误差Table 4 Size of disc springs and the predicting error of flattening load

4.2 碟形弹簧回弹方程预测模型

与压平载荷预测模型研究方法相同，各影响因素的物理量量纲如表5所示，应用定理，将各物理量写成无量纲准数的形式，相应的公式可以表示为

(18)表5 各物理量量纲分析Table 5 Dimensional analysis of physical quantities

根据25组碟形弹簧回弹段载荷-位移计算结果，拟合得到碟形弹簧回弹方程预测模型：

F/(d2E)=560 669.6(h/d)1.6(t/d)2.3·

exp(-17.6α)C-4μ0.7

(19)

使用3个不同结构参数的碟形弹簧对该回弹方程预测模型进行验证，碟形弹簧具体尺寸如表4所示，由回弹方程预测模型得到的回弹曲线与模拟得到的回弹曲线如图13—15所示。

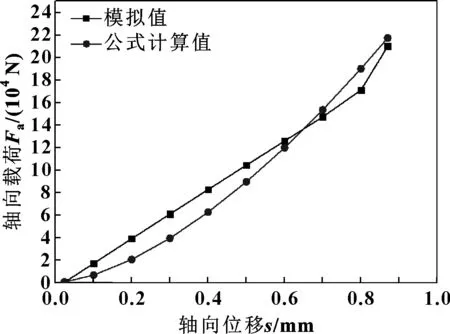
图13 模型1回弹段公式计算值与模拟值对比Fig 13 Comparison of formula calculation value and simulation values of Model 1 springback section

图14 模型2回弹段公式计算值与模拟值对比Fig 14 Comparison of formula calculation values and simulation values of Model 2 springback section

图15 模型3回弹段公式计算值与模拟值对比Fig 15 Comparison of formula calculation values and simulation values of Model 3 springback section

由图13—15可知，3组碟形弹簧模型的回弹部分公式计算值与模拟值较为接近，说明该回弹方程预测模型是可靠的。

5 结论

(1)通过ABAQUS有限元分析软件确定了螺栓法兰接头用碟形弹簧力学性能有限元分析方法。

(2)研究了碟簧各结构参数对其压缩回弹性能的影响，研究结果表明：碟簧的压平载荷随碟簧厚度、倾角的增加呈上升趋势，随外内径比的增加呈下降趋势；回弹率随碟簧厚度、倾角、外内径比的增加均呈下降趋势。

(3)基于正交试验和量纲分析法，建立了螺栓法兰接头用碟形弹簧压平载荷以及回弹曲线预测模型，经验证误差在5%以内。