基于GM(1,1)-MC的大坝变形预测模型
2019-10-22李苗
李苗
基于GM(1,1)-MC的大坝变形预测模型
李苗
(江西水利职业学院,江西 南昌 330013)
针对灰色模型GM(1,1)受随机扰动较大影响模型预测精度这一问题,提出一种基于灰色马尔科夫链的状态转移预测模型。在GM(1,1)模型预测结果的基础上,利用马尔科夫链(MC)对残差序列进行误差修正,建立灰色马尔科夫GM(1,1)-MC组合状态转移预测模型。通过对水布垭大坝沉降变形预测结果分析表明,GM(1,1)-MC预测结果更接近实测值,该模型能有效提高预测精度。
大坝变形;灰色模型;马尔科夫链;GM(1,1)-MC模型
1 引言
变形监测是大坝安全监测中的一项重要内容,大坝变形作为大坝安全性态的一项重要指标,为大坝安全运行提供决策[1]。近年来随着计算机的飞速发展,灰色模型、BP神经网络、支持基向量、卡曼滤波、小波分析等在大坝变形预测中得到广泛应用,预测模型对分析大坝变形起到一定作用,同时进一步推动大坝安全监测的发展。灰色模型在数据序列短、信息量少、数据波动性不大时预测精度较高,但是大坝变形监测中,观测数据随时间的推移扰动性逐渐增大,这将影响预测精度。
马尔科夫链(MC)不受过去状态的影响,状态转移概率ij能够反映随机扰动的影响程度[2]。因此,MC适用于受随机扰动较大的动态预测,同时可以弥补GM(1,1)预测模型的不足。利用GM(1,1)模型对初始数据进行预测拟合,并对残差序列采用MC模型预测,实现GM(1,1)模型与MC模型两者的优势互补。本文将GM(1,1)-MC模型应用于水布垭大坝坝体沉降变形预测,进一步验证其适用性和可靠性。
2 建立GM(1,1)-MC预测模型
2.1 灰色GM(1,1)模型原理
灰色GM(1,1)预测模型基于灰色系统理论[3],可有效解决小样本、贫信息的数据预测。
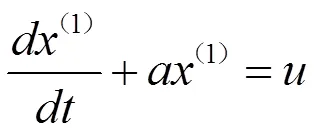
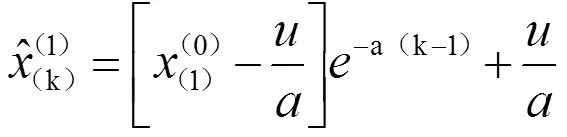
利用累减得到原始数据序列(0)的预测函数:
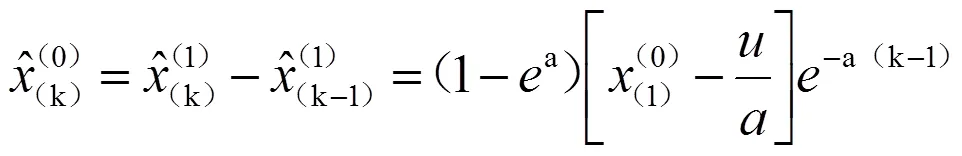
=1,2,…,
2.2 马尔科夫链(MC)误差修正模型
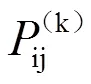
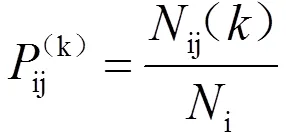
式(2)中:ij()为i经步转移到j的次数;i为状态i的总次数。在统计i时,由于最后一个序列的发展状态未知,因此,要把最后个状态剔除,则第步序列的状态转移概率矩阵()可表示为:
选取预测值前个实测值(=),根据状态转移概率矩阵中的第(=1,2,…,)个实测值经(=,1,…,1;+=+1)步转移到预测值状态的概率,把个概率进行求和,最大值的相对误差状态为预测值相对误差所处状态。
确定预测值相对误差所属状态即预测值所属状态,对GM(1,1)预测值进行误差修正:
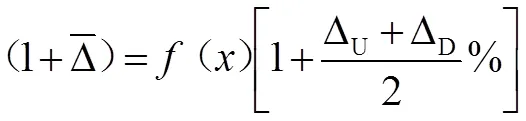

3 工程实例应用
水布垭水电站是目前世界在建和已建最高混凝土面板堆石坝,共选取18组沉降数据进行预测分析。整个建模预测过程采用MATLAB软件编程实现,相对误差预测状态如表1所示。2014-07-21的预测值处于3状态,据马尔克夫残差修正理论公式(3),可计算出2014-07-21的坝体内部沉降变形GM(1,1)-MC预测值为1 152.55 mm,实测值为1 153.61 mm,GM(1,1)模型预测值为1 151.36 mm,GM(1,1)-MC模型预测值为1 152.5 mm与实测值更接近,因此,该模型可有效地提高预测精度,以此类推可求出其他日期的GM(1,1)-MC模型预测值,如图1所示。
由图1可知,GM(1,1)-MC模型预测值与真实值更为接近,而GM(1,1)模型预测值与真实值偏差较大,表明GM(1,1)-MC模型预测精度高于GM(1,1)单一模型预测。
为进一步验证GM(1,1)-MC模型的优越性,引入相关系数2和均方差MSE对两种模型拟合度进行综合评价。
GM(1,1)单一模型预测结果2=0.939,MSE=0.066;而GM(1,1)-MC模型预测结果2=0.987,MSE=0.028,因此,进一步验证了GM(1,1)-MC模型综合性能和精度均较高。
表1 2014-07-21相对误差预测状态
观测日期转移时步所属状态E1E2E3E4 2014-06-231E11/31/301/3 2014-05-222E201/21/20 2014-04-243E31/31/31/30 2014-03-194E40013 概率统计 0.6671.1671.8330.333
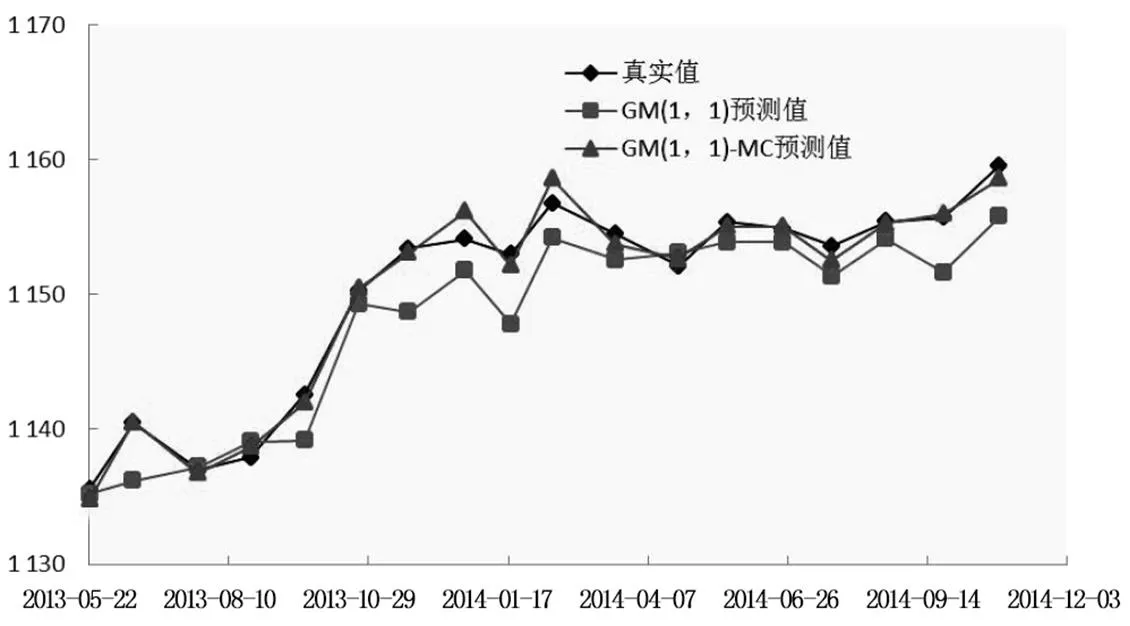
图1 GM(1,1)和GM(1,1)-MC模型拟合曲线
4 结论
本文提出将MC引入灰色GM(1,1)模型中,对其残差进行修正,建立了基于马尔科夫灰色GM(1,1)-MC坝体内部沉降预测模型,并通过水布垭工程实例将该模型与GM(1,1)模型进行对比。结果表明,GM(1,1)-MC组合模型拟合度及预测精度均较高,在大坝安全监测中有一定实用价值。
[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[2]何成刚.马尔科夫模型预测方法的研究及其应用[D].合肥:安徽大学,2011.
[3]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.
[4]周从华.随机模型检测理论与应用[M].北京:科学出版社,2014.
TV698.1
A
10.15913/j.cnki.kjycx.2019.19.010
2095-6835(2019)19-0029-02
李苗(1990—),女,山西运城人,硕士研究生。
〔编辑:严丽琴〕
