强风激励下建筑自振特性测试与分析——以防灾科技学院6号教学楼为例＊

肖爽，王小明

强风激励下建筑自振特性测试与分析——以防灾科技学院6号教学楼为例＊

肖爽，王小明

（上海市地震局，上海 200062）

建筑物的动力特性是建筑物自身固有的特性，一般是指建筑物的振动频率（或者振动周期）、振型及阻尼比。建筑物的地震反应是由地面运动的性质和结构本身的动力特性决定的。因此在计算地震反应时，结构的自振频率、振型及阻尼比都是十分重要的参数。由于理论计算方法求得的结构自振频率存在误差，所以利用现场实测得到的结构动力特性即建筑物建成后的实际动力特性，其结果是准确、可靠的。通过对防灾学院6号教学楼进行强风振动测试实验，获取了南北和东西两个方向的加速度时程数据，利用DASP数据处理软件对所获得的数据进行了低通滤波（25 Hz），通过在频域内对数据进行分析和计算给出了该教学楼1～3阶固有频率、振型和阻尼比，得到强风作用下结构的平动特性，与环境激励（地微动）作用下结构的自振特性进行对比，最后总结出有意义的结论，用于建立该结构的结构健康档案，并为结构健康监测提供参考。

环境振动测试；模态分析；固有频率；阻尼比

随着社会的不断发展，建筑物的健康检测和损伤识别对建筑有着至关重要的意义。由于建筑物的动力特性一般是指建筑物的振动频率（振动周期）、振型及阻尼比，而建筑物的地震反应是由地震运动的性质和结构自身的动力特性定共同决定的。因此，在计算地震反应时，结构的自振频率、振型及阻尼比都是十分重要的基本参数。理论计算参数的方法是通过简图计算得到的数据，然而简图一般比较简化，通常填充墙等非结构部件不计入结构刚度中，而且结构的质量分布、材料的实际性能、施工质量等都不能准确计算。所以，通过利用现场实测得到的建筑动力特性，即建筑物建成后的实际动力特性，其结果是准确、可靠的。

本文所采用的实验方法是环境振动测试实验，在整个测试过程中不会对建筑物造成任何影响和损害，通过频域分析法和时域分析法进行模态参数分析，计算出该教学楼1～3阶固有频率、振型和阻尼比，利用规范计算出实际的地震作用值，与实验数据得到的强风作用下的地震作用进行对比，最后总结出有意义的结论。

防灾科技学院6号教学楼为12层框架剪力墙建筑，东西长70 m，高45 m左右。该教学楼为多功能楼，裙楼为3层，主要是阶梯教室，1～6、9、10楼为学生正常上课场所，7、8楼为实验室，11层为机房，12层主要是网络办公室。该教学楼作为学院内学生上课活动的主要场所，其在学院内的作用是很大的，因此有必要了解该楼的模态参数，为该楼日后进行健康监测提供数据资料。从卫星图上看该楼北临海油大街、西临燕灵路，这两条道路在上下班高峰期间的车流量很大，因此笔者认为对该建筑物振动有影响的因素有以下几点：①上下课期间大量学生的走动；②由于紧邻道路，上下班高峰期时车辆的大量流动；③安装在建筑物地下一层的供水泵工作时的振动。此外还有自然环境因素，尤其在春冬季北方大风时，由于南北方向的楼梯较窄，南北方向的大风会加剧建筑物的振动。所以，本文即采用脉动法对防灾科技学院6号教学楼进行自振特性测试与分析。

1 实验方法和实验过程

1.1 实验方法（环境振动测试）

脉动试验是现时广泛采用的试验方法，这是由于高灵敏度传感器捡拾到的振动信号与高性能的分析仪器的配合，已经能够很好地满足测量与分析的需要。无需利用起振机等激振手段便能得到所需结果。

建筑物的脉动是一种很微小的振动，振动源来自地壳内部微小的振动，地面车辆运动、机器运转所引起的微小振动以及风引起的建筑物的振动等，利用建筑物的脉动响应来确定其动力特性，俗称脉动试验。利用高灵敏度的传感器、放大记录设备，借助于随机信号数据处理的技术，利用环境激励量测结构物的响应，分析确定结构物的动力特性是一种有效而简便的方法，它可以不用任何激振设备，对建筑物丝毫没有损伤，也不影响建筑物内正常工作的进行，在自然环境条件下就可以量测建筑物的响应，经过数据分析就可以确定其动力特性。

本实验即采用脉动试验法，在强风的自然环境激励下对学院6号教学楼进行自振特性测试，得出结果分析结论。

1.2 实验环境及过程

实验当日风速为11.78 m/s，相当于5级强风下，做强风激励下学院6号教学楼自振特性测试。实验时用实验设备941B型拾振器12台，941型放大器2台，INV306U型采集仪1台，安装有数据采集系统的笔记本电脑1台。

首先做了6号楼平动自振特性测试，将12个传感器分别安放在1～12层楼楼层的几何中心位置，其目的是让传感器接收到的信号仅仅是平移振动信号，扭转振动信号不要进来，这样在做数据分析处理时便于识别平移振动信号。按照传感器布置的原则，自下而上按照楼层等间隔的安放传感器，也要考虑到特殊部位传感器的安放，如果一个传感器应振动的方向是，两个方向的，则一次就可记录下两个方向的振动。一般传感器多为感受某一个方向的振动，因此，可以先测定一个方向的振动，等记录完毕后再把传感器在平面上转动900，再测另一个方向的振动，本实验即做了6号楼南北以及东西两个方向的平动测试实验。平动测试拾振器布置如图1所示。

由于地震破坏的实际事例中，建筑物由于扭转振动导致损坏的例子并不少见，因此尽量减少结构的扭转效应也是在设计中应该注意的，因此做了扭转作用下6号楼的振动测试实验。平移振动布置测点与扭转振动布置测点不同，建筑物的扭转振动是整个建筑物绕着结构的扭转中心在转动，因此它越远离扭转中心，振动也就越大。所以，往往把扭转振动的测点布置在建筑物的最边端，即建筑物的两侧，在一个楼层中成双成对地布置测点。

扭转测试拾振器布置如图2所示。

图1 平动测试拾振器布置图

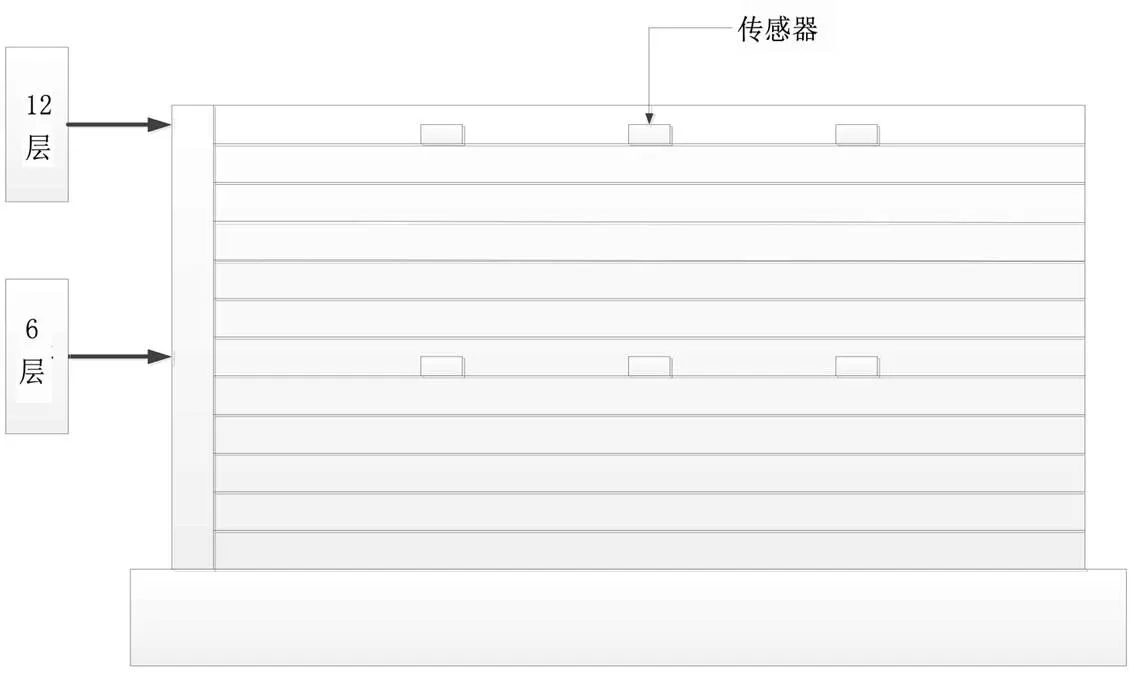
图2 扭转测试拾振器布置图

1.3 实验数据

由北京振动与噪声研究所研发的DASP数据处理软件进行谱分析，得到振动测试的幅值，与转换系数计算得到6号教学楼在平动情况下实际的位移、速度以及加速度值如表1所示。

表1 相关实验数据结果

通道号安静（无风）平动位移/m安静（大风）平动位移/m安静（无风）平动速度/（m/s）安静（大风）平动速度/（m/s）安静（无风）平动加速度/（m/s2）安静（大风）平动加速度/（m/s2） 14.94×10－71.54×10－64.71×10－67.70×10－64.26×10－45.17×10－4 21.04×10－62.64×10－67.90×10－61.46×10－54.93×10－46.76×10－4 31.57×10－63.93×10－61.07×10－52.25×10－53.46×10－45.74×10－4 42.27×10－66.74×10－61.41×10－53.10×10－54.56×10－47.05×10－4 52.92×10－67.33×10－61.75×10－53.84×10－57.90×10－49.73×10－4 63.63×10－69.04×10－62.02×10－54.39×10－57.84×10－49.81×10－4 74.44×10－61.15×10－52.36×10－54.71×10－57.4×10－41.04×10－3 84.72×10－61.14×10－52.56×10－55.67×10－51.01×10－31.14×10－3 95.69×10－61.33×10－52.92×10－56.11×10－51.10×10－31.30×10－3 105.50×10－61.14×10－52.70×10－55.56×10－59.01×10－41.21×10－3 116.89×10－61.52×10－53.14×10－55.86×10－51.04×10－31.25×10－3 127.63×10－61.71×10－53.60×10－56.18×10－51.18×10－31.40×10－3

2 振动测试结果分析

2.1 地震作用力算法介绍

根据《建筑抗震设计规范》，求得多质点弹性体系的水平地震作用的计算可采用振型分解反应谱法，在一定条件下还可以采用比较简单的底部剪力法。

2.1.1 振型分解反应谱法

体系振型质点水平地震作用标准值计算公式为：

ji=jjiji（=1，2，…，；=1，2，…，） （1）

式（1）中：为相应振型自振周期的地震影响系数；ji为振型质点的水平相对位移；j为振型的振型参与系数；i为质点的重力荷载代表值。

2.1.2 底部剪力法

底部剪力法的计算公式为：

EK=1eq（2）

式（2）中：eq为结构等效总重力荷载代表值，0.85g；为结构总重力荷载等效系数（规范约取0.85）。

根据《建筑抗震设计规范》可知，在这两种方法计算中都需用到地震影响系数的值，而建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构自振周期以及阻尼比确定，要想得到完整的地震影响系数谱曲线，则需要通过实验来测得结构的自振周期和同一周期不同质点的相对位移比值，通过实际测得的实验数据计算准确的水平地震作用。地震影响系数谱曲线如图3所示。

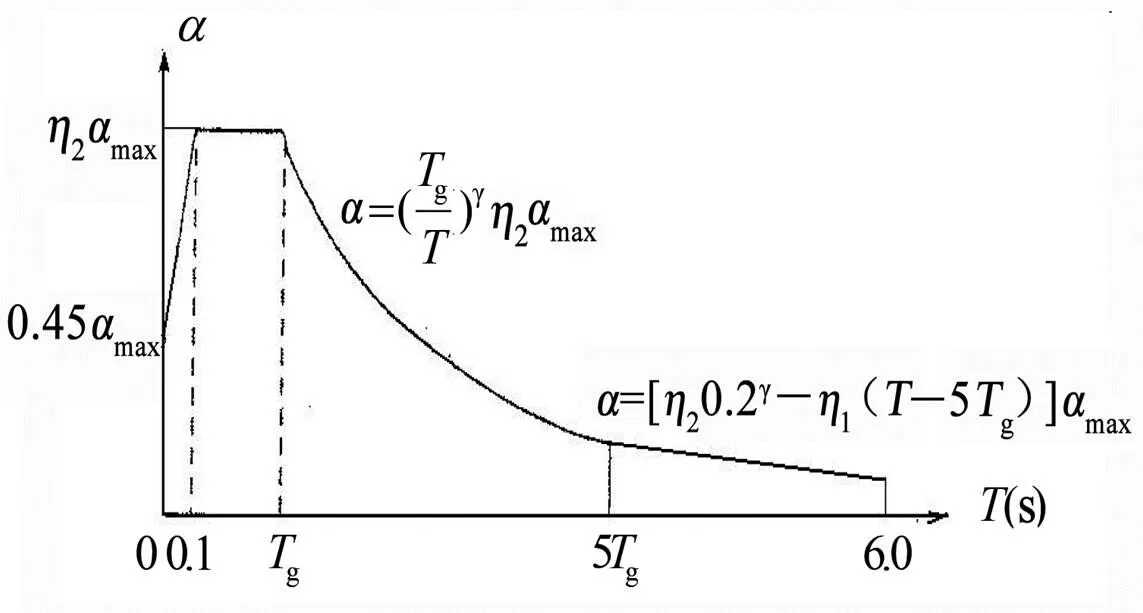
图3 地震影响系数谱曲线

图3中，为地震影响系数，g为特征周期，为结构周期，为曲线下降段的衰减指数，2为阻尼调整系数，max为地震影响系数最大值，1为直线下降段的斜率调整系数，小于0.55时取0.55。

2.2 互功率谱分析

根据北京振动与噪声研究所研发的DASP数据处理软件进行谱分析，可得到6号教学楼的功率谱，功率谱定义为单位频带内的信号功率，它表示了信号功率随着频率的变化情况，功率谱的曲线一般横坐标为频率，纵坐标为功率。利用峰值法分析出建筑物的固有频率，峰值法是一种频域分析法，其实质是建筑物在固有频率会产生很大的响应，功率谱上的峰值点对应的频率中识别出建筑的自振频率，无论是测点的自谱或两个信号的互谱，在建筑物固有频率处都会出现陡峭的峰值，建筑物固有频率就是利用这一特性来确定的。防灾科技学院6号教学楼在南北方向的平动谱分析如图4～图15所示，以第三质点为参考点，选择前25 Hz频率进行互功率谱分析选取的前三阶固有频率的互谱分析图，由于功率没有负值，所以根据相位的大小确定方向，相位度数接近于180°或180°的倍数时为相反方向；反之即为同向。

2.3 振型图

根据互功率谱分析图整理数据，确定南北方向平动的情况下，对于6号教学楼各质点的功率与频率的对应关系，由于功率与各质点的位移有关，所以功率的大小可以代表各质点的位移量，相位度数的大小可以确定质点的位移方向，利用Excel整理出第一、第二、第三振型的频率与其相对应各质点的相对位移并绘制出其振型图，如图16、图17、图18所示，前三振型各质点的相对位移如表2所示。

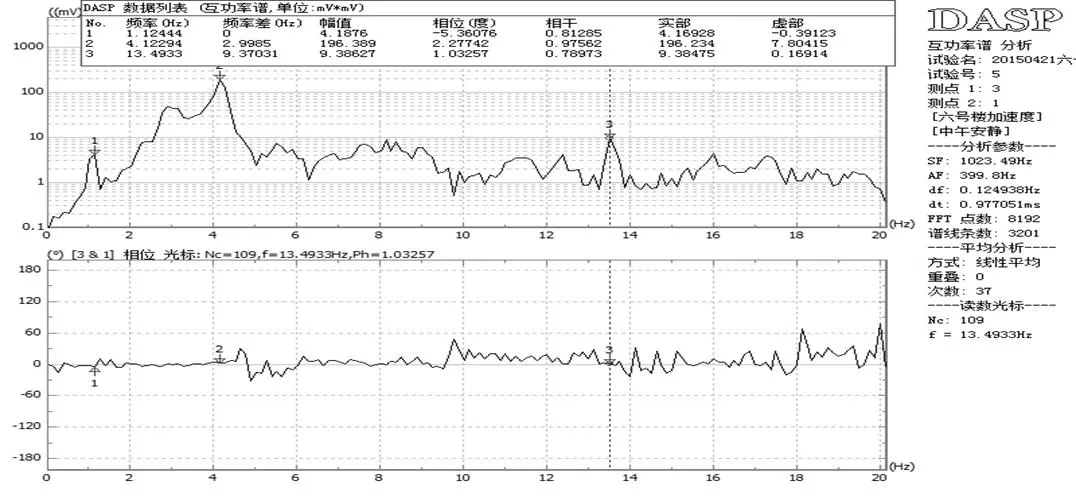
图4 第一层质点平动互谱功率分析图

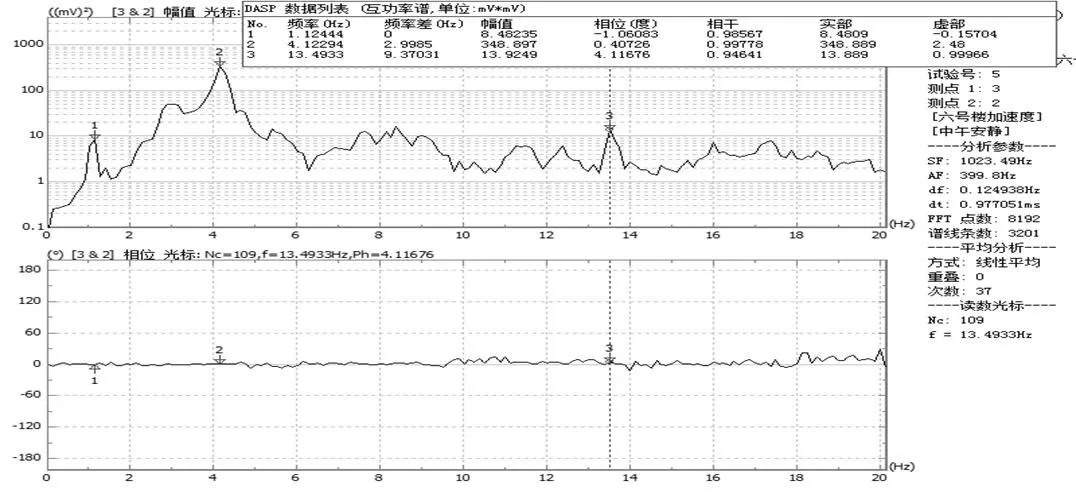
图5 第二层质点平动互谱功率分析图

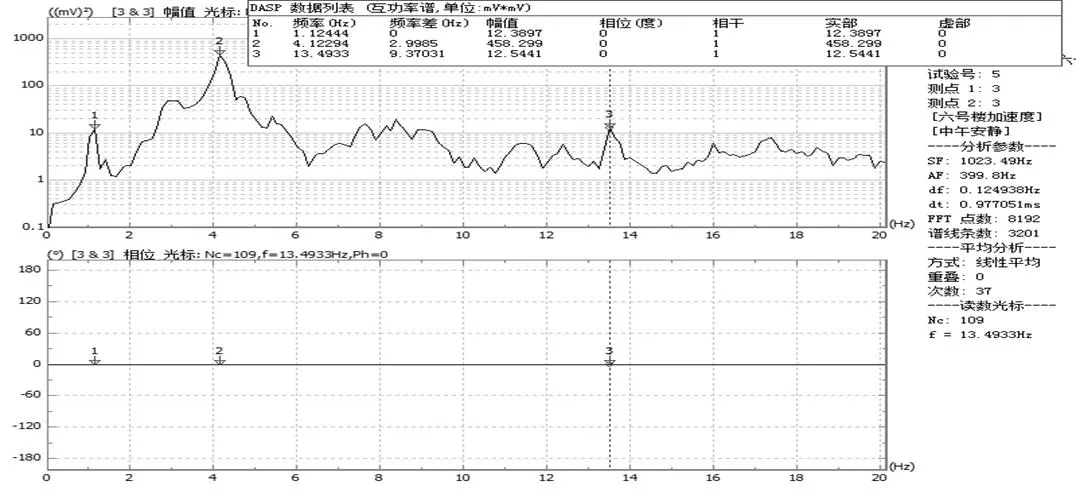
图6 第三层质点平动互谱功率分析图

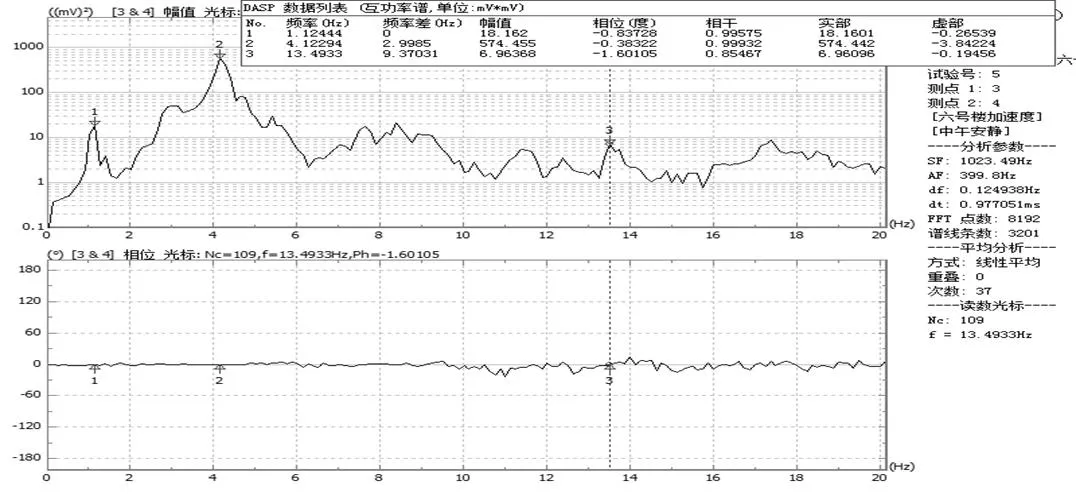
图7 第四层质点平动互谱功率分析图

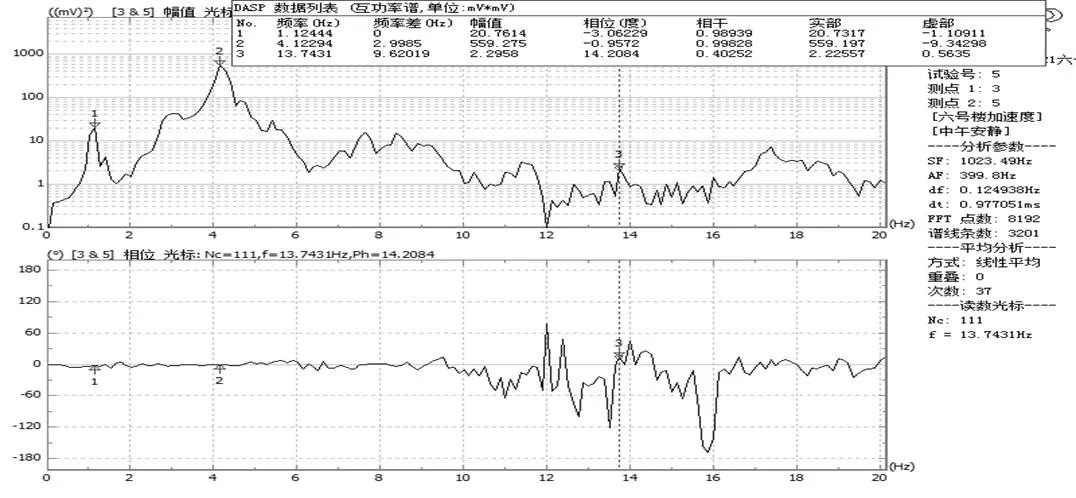
图8 第五层质点平动互谱功率分析图

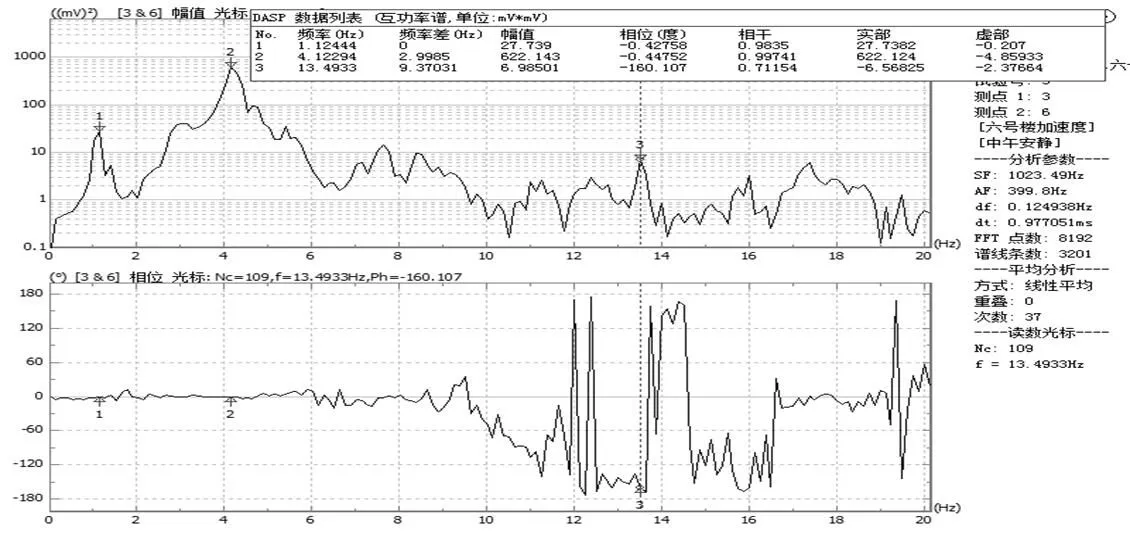
图9 第六层质点平动互谱功率分析图

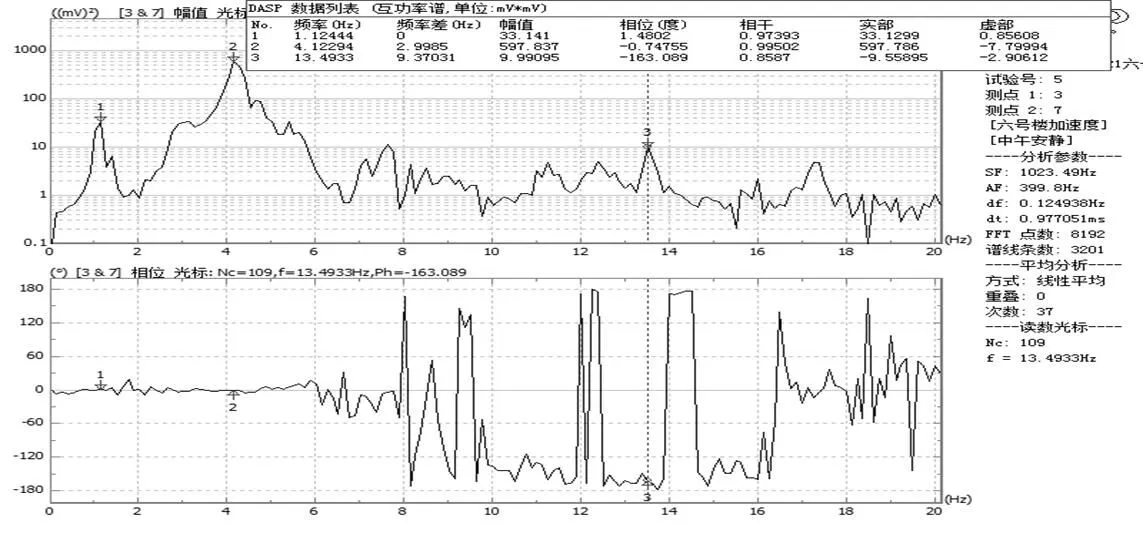
图10 第七层质点平动互谱功率分析图

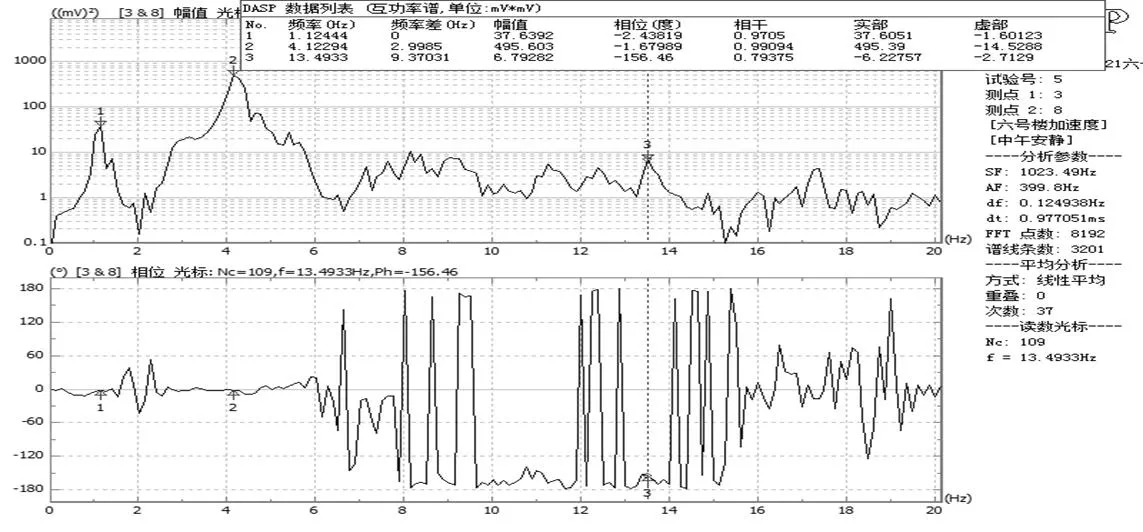
图11 第八层质点平动互谱功率分析图

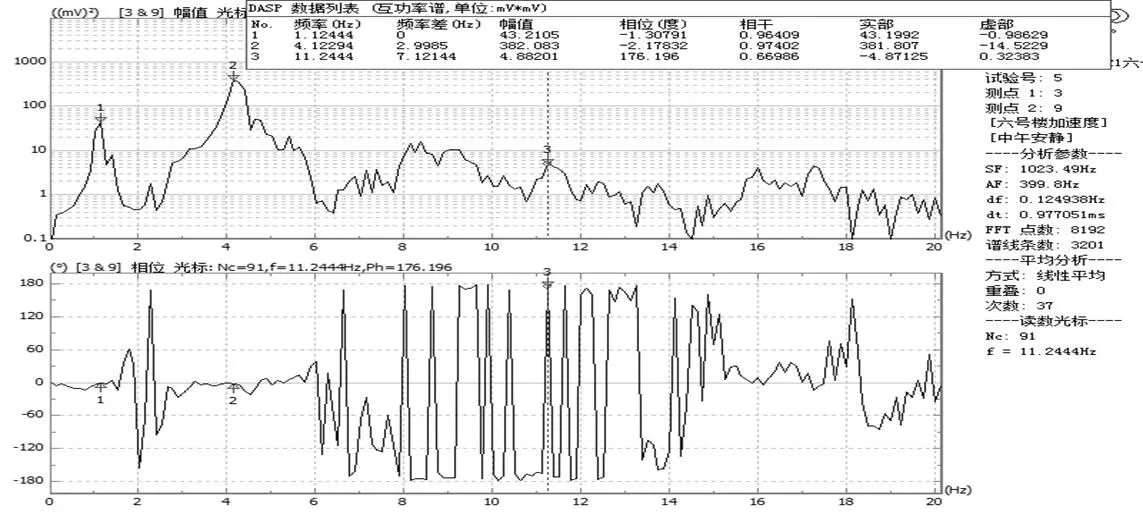
图12 第九层质点平动互谱功率分析图

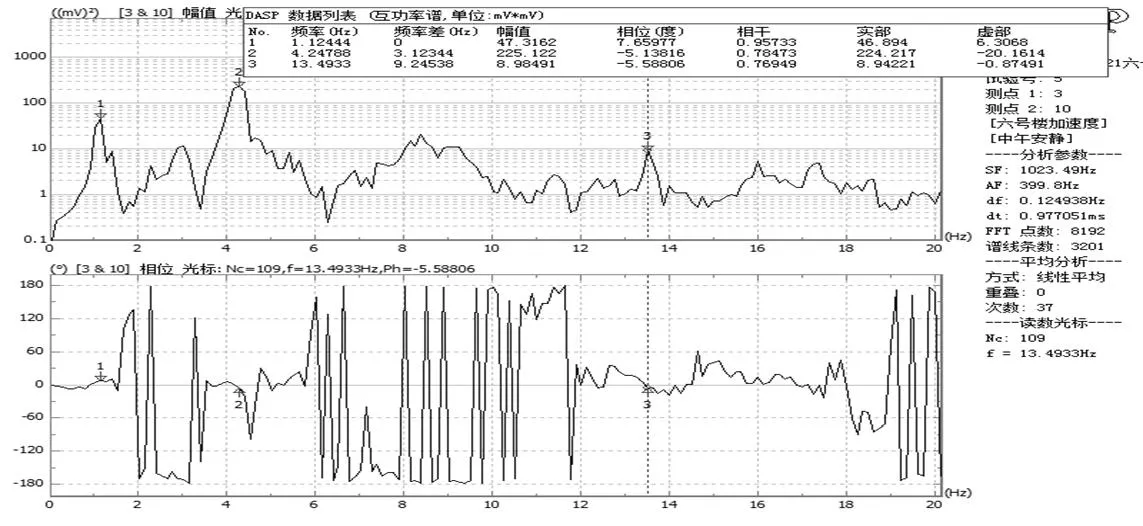
图13 第十层质点平动互谱功率分析图

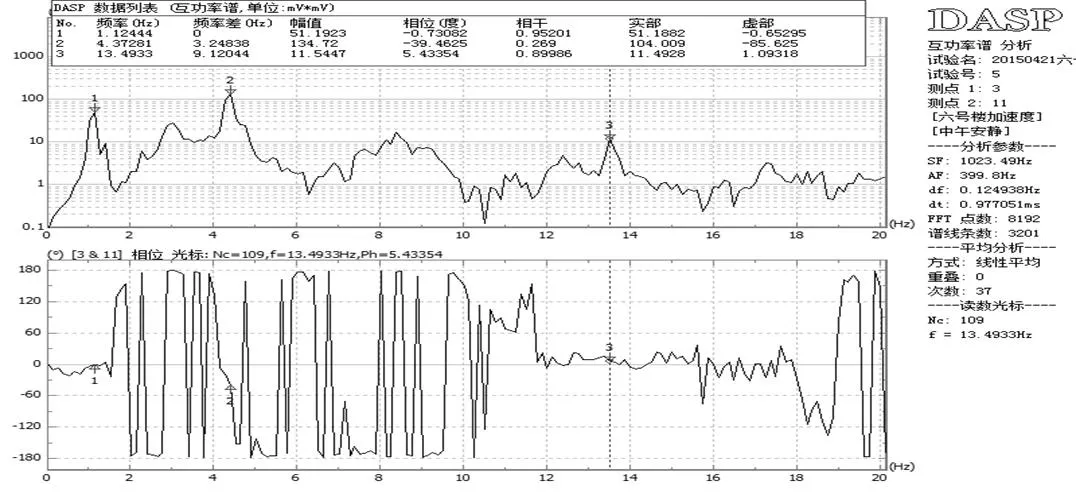
图14 第十一层质点平动互谱功率分析图

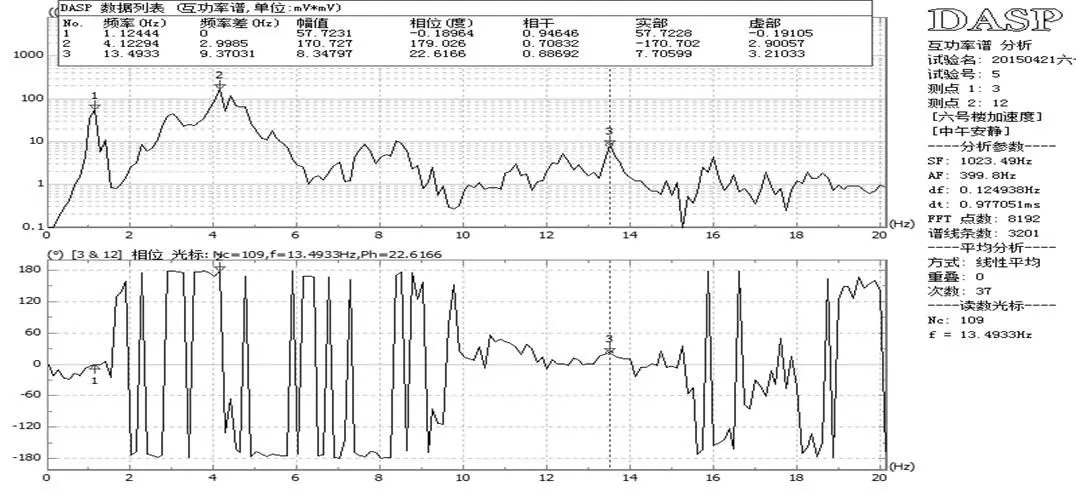
图15 第十二层质点平动互谱功率分析图

表2 前三振型各质点的相对位移表

质点第一振型各质点位移第二振型各质点位移第三振型各质点位移 14.187 6196.3899.386 27 28.482 35348.89713.924 9 312.389 7458.29912.544 1 418.162574.4556.963 68 520.761 4559.2752.295 8 627.739622.143﹣6.985 01 733.141597.837﹣9.990 95 837.639 2495.603﹣6.792 82 943.210 5382.083﹣4.882 01 1047.316 2225.1228.984 91 1151.192 3134.7211.544 7 1257.723 1﹣170.7278.347 97

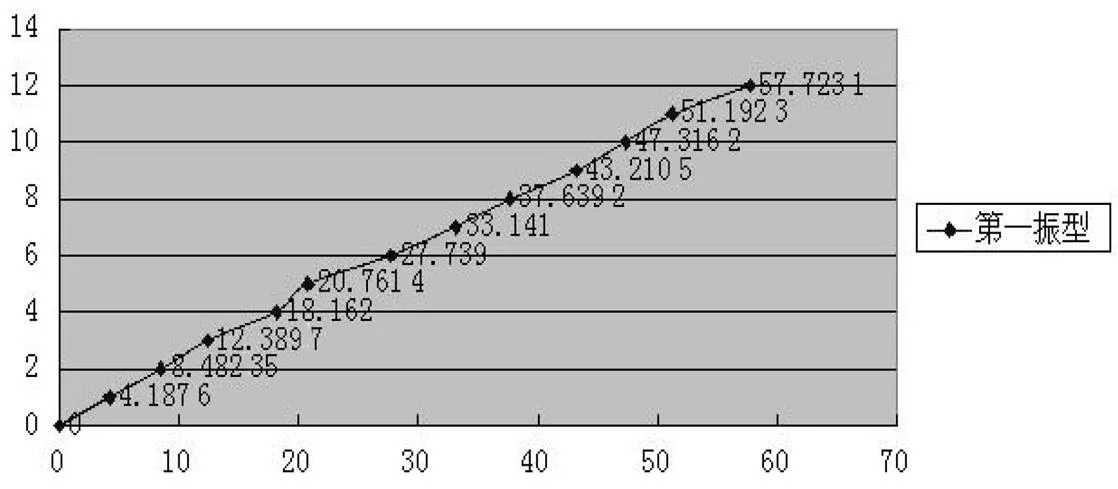
图16 第一振型（f1=1.124 44）的振型图

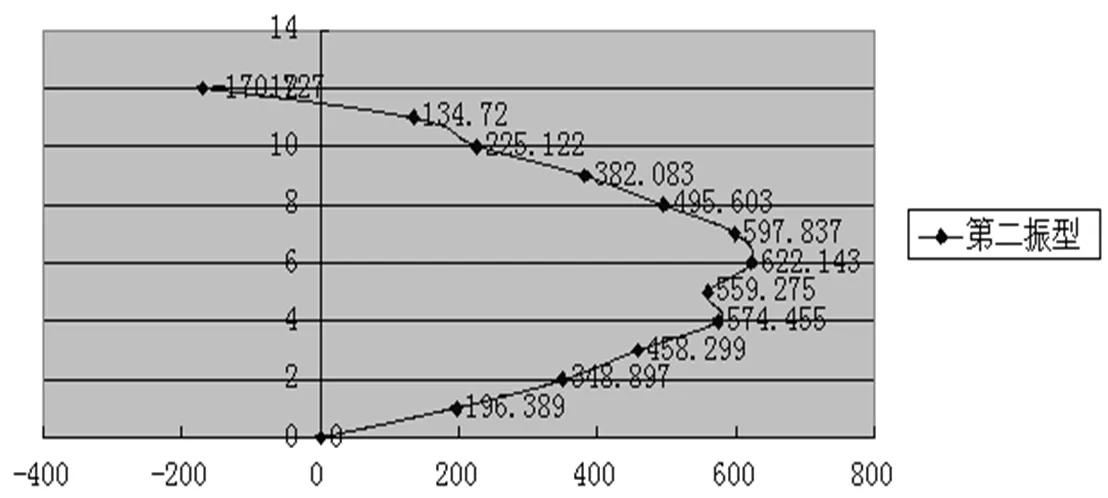
图17 第二振型（f2=4.154 17）的振型图

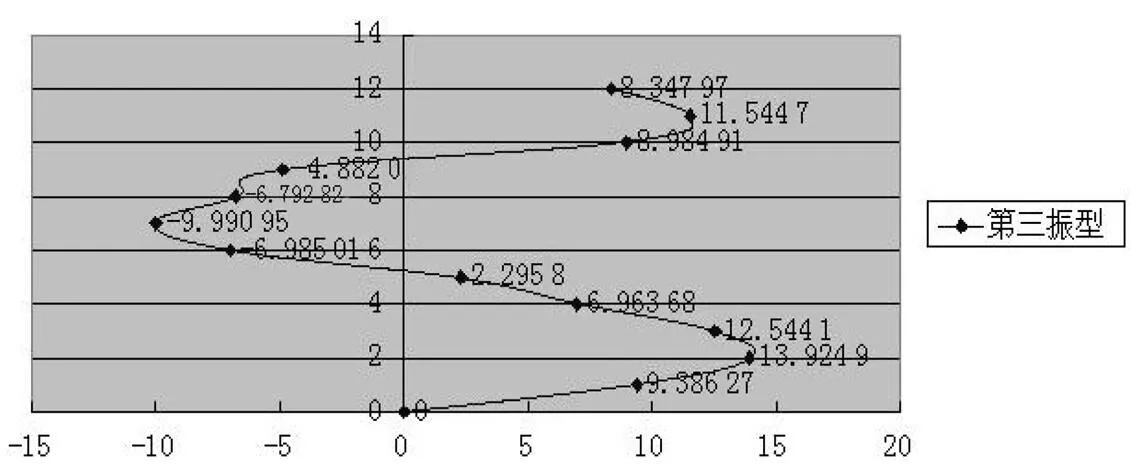
图18 第三振型（f3=13.326 7）的振型图

2.4 水平地震作用力分析与计算

根据6号教学楼建筑说明可知，6号教学楼抗震设防烈度为8度，设计基本地震加速度为0.2 m/s2，设计地震分组为第一组，建筑物场地类别为Ⅲ类。

计算得出6号教学楼结构总重力荷载为68 684 kN，每层重力荷载标准值i为5 723.67 kN，以下分别采用两种方法计算建筑物水平地震作用力。

2.4.1 实验计算结果

根据特征周期、特征周期值表可知，max=0.16，g= 0.45 s，可得到6号教学楼地震影响系数曲线，如图19所示。

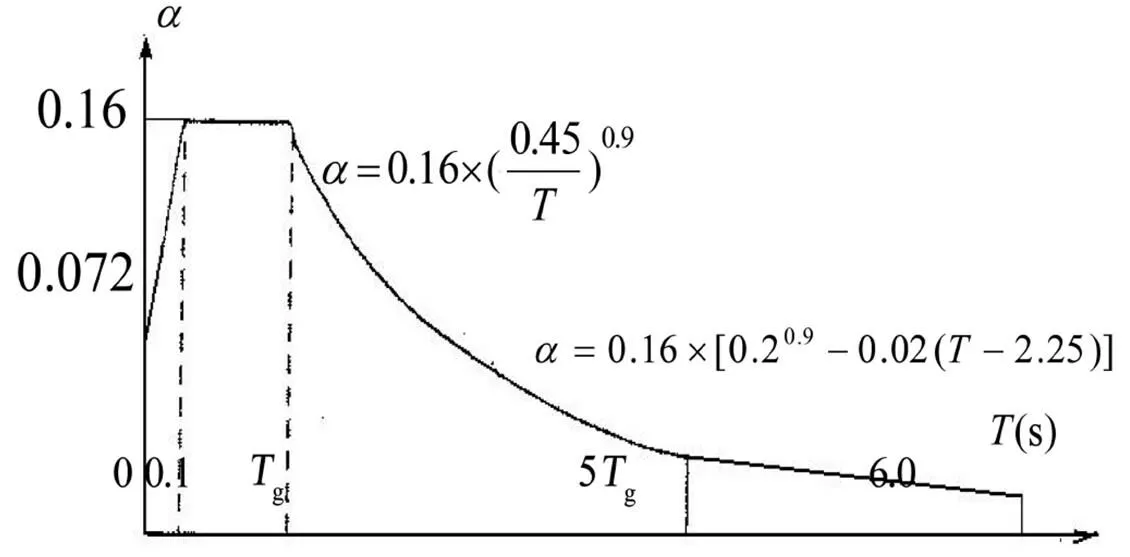
图19 6号教学楼地震影响系数曲线

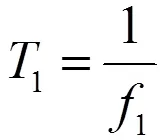
利用底部剪力法计算结构总水平地震作用标准值EK=1×eq=0.087×58 381.4=5 079.18 kN。

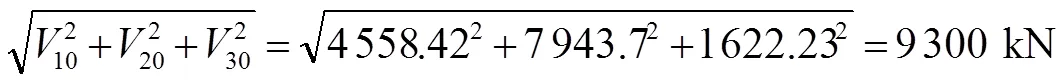
2.4.2 理论计算结果

根据《建筑结构荷载规范》附录F结构基本自振周期的经验公式F.2.2，钢筋混凝土框架和框剪结构的基本自振周期按下式计算：

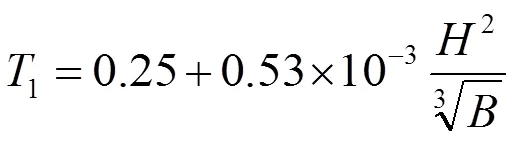
式（3）中：为房屋总高度，m；为房屋宽度，m。

根据6号楼建筑图纸得到数据=53 m，（最窄受风面）。因此，1=0.84 s，2=0.28 s，3=0.168 s。

利用底部剪力法计算结构总水平地震作用标准值EK=1×eq=0.09×58 381.4=5 254.326 kN。

3 振动测试实验结论

经过对学院6号教学楼环境激励下振动测试试验及振动数据的处理，从3个方面对实验结果进行对比分析。

3.1 振动量分析

通过时域分析获取了地脉动激励和强风激励下结构的振动量值。

在无风条件下，南北方向的最大平动位移=5.69×10﹣6m，最大平动速度=3.60×10﹣5m/s，最大平动加速度=1.18×10﹣3m/s2。

在有风条件下，风速度风=11.78 m/s，相当于5级强风下，南北方向的最大平动位移=1.71×10﹣5m，最大平动速度=6.18×10﹣5m/s，最大平动加速度=1.40×10﹣3m/s2。

3.2 前三阶自振周期分析

通过频域分析，获取了地脉动激励和强风激励下结构的前三阶自振周期。

南北方向在无风振动情况下，第一振型自振周期1=0.889 s；第二振型自振周期2=0.24 s；第三振型自振周期3=0.075 s。

南北方向在有风振动情况下，风速度风=11.78 m/s，相当于5级强风，第一振型自振周期1=0.94 s；第二振型自振周期2=0.25 s；第三振型自振周期3=0.075 s。

根据《建筑结构荷载规范》的高层建筑钢筋混凝土框架和框剪结构的基本自振周期计算得到，第一振型自振周期1=0.84 s，第二振型自振周期2=0.28 s，第三振型自振周期3=0.168 s。

通过上述结论分析，在同一方向、建筑物下进行振动测试，有风和无风的情况下的结构自振周期基本相同，由此可知，结构的自振周期是结构本身的动力特性，它只与楼层的高度、质量、构件布置等物理量有关，与外界的作用力无关。通过对比可知，实验的自振周期值与《建筑结构荷载规范》的自振周期值基本相似。

3.3 底层地震剪力对比分析

估算与实测结构自振特性获取的底层地震剪力对比分析如下。

根据实测结构的自振周期1=0.889 s，利用底部剪力法计算结构总水平地震作用标准值EK=5 079.18 kN；根据《建筑结构荷载规范》估算的结构自振周期1=0.84 s，利用底部剪力法计算结构总水平地震作用标准值EK=5 254.326 kN。 根据实验数据与规范中的数据分别利用底部剪力法计算总水平地震作用标准值十分接近，可分析出实验的第一振型与规范中的第一振型基本相似。

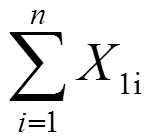
4 总结

本文采用脉动实验方法，利用DASP数据处理软件谱分析，初步得到建筑物有风、无风时的位移、速度、加速度实验结果，然后选择前25 Hz频率进行互功率谱分析选取前三阶固有频率的互谱分析图，得到该建筑物前三阶振型自振频率和振型图。通过对实验数据计算的该建筑物实测水平地震作用力和《建筑结构荷载规范》计算出的理论水平地震作用力进行对比分析，发现计算结果十分接近。

通过脉动实验结果对比发现，有风和无风情况下的结构自振周期基本相同，证实结构的自振周期是结构本身的动力特性，它只与楼层的高度、质量、构件布置等物理量有关，与外界的作用力无关。利用实验测得结构一阶自振周期计算的结构水平地震作用力值与《建筑结构荷载规范》估算的自振周期计算的结构水平作用力值接近。本文的实验和计算方法对建筑物结构健康监测具有参考价值。

［1］徐培福，肖从真，李建辉.高层建筑结构自振周期与结构高度关系及合理范围研究［J］.土木工程学报，2014（2）：1-11.

［2］施卫星，魏丹，韩瑞龙.钢结构房屋动力特性脉动法测试研究［J］.地震工程与工程振动，2012（1）：114-120.

［3］刘红彪，郭迅，梁永朵，等.9度设防区房屋结构自振周期测试［J］.建筑结构，2011（5）：60-62，77.

［4］方鄂华，钱稼茹，马镇炎.高层钢结构基本周期的经验公式［J］.建筑结构学报，1993（2）：56-62.

［5］中华人民共和国住房和城乡建设部.GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［6］中国工程建设标准化协会.建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012.

U441.3

A

10.15913/j.cnki.kjycx.2019.19.003

2095－6835（2019）19－0006－06

肖爽（1993—），女，防灾科技学院土木工程学士学位，上海市地震局助理工程师，主要研究方向为地震应急、建筑抗震设计。

王小明。

上海市科委项目（18DZ1200500）资助

〔编辑：张思楠〕