论数学核心素养下高阶思维的培养

陈丽

摘 要：数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。数学高阶思维是指发生在数学思维活动中的较高认知水平层次上的心智活动或认知能力，在教学目标分类中表现为分析、综合、评价和创造。文章阐述了数学核心素养的内涵、数学核心素养下的高阶思维，并提出了加强数学阅读能力的培养、发散思维一题多解、强化分类讨论思想等培养学生的数学高阶思维的方法。

关键词：中学数学;数学核心素养;高阶思维

教育部印发的《关于全面深化课程改革，落实立德树人根本任务的意见》中，明确界定了学科核心素养，即学生应具备的适应终身发展和社会发展需要的必备品格和关键能力。《普通高中数学课程标准（2017年版）》明确提出了中学数学的六大核心素养，并围绕学科核心素养的落实，精选、重组教学内容，设计教学活动，提出考试评价的建议，目的是切实引导各学科教学在传授学科知识过程中，更加关注学科思想、思维方式等，把立德树人根本任务落到实处。

一、数学核心素养的内涵

高考突出核心价值、学科素养、关键能力、必备知识等考查内容，尤其值得关注的是学科素养。对学科核心素养的考查，将是今后高考的命题热门。数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。

数学抽象是指舍去事物的一切物理属性，得到数学研究对象，利用图形理解和解决数学问题的思维过程;逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的思维过程;数学建模是指学生通过实际应用问题，运用数学语言，清晰、准确地表达数学建模的过程;数学运算是指学生通过各类数学问题特别是综合性问题，明确运算对象，分析运算条件，选择运算法则，把握运算方向，设计运算程序，获取运算结果的过程;直观想象是指学生通过空间图形与平面图形的观察以及图形与数量关系的分析，通过想象对复杂的数学问题进行直观表达，运用图形和空间想象思考问题，感悟事物的本质，形成解决问题的思路的思维过程;数据分析是指学生通过对概率与统计问题中大量数据的分析和加工，获得数据提供的信息及其所呈现的规律，进而分析随机现象的本质特征，发现随机现象的统计规律的思维过程。

二、数学核心素养下的高阶思维

高阶思维，是发生在较高认知水平层次上的心智活动或较高层次的认知能力;高阶思维是高阶能力的核心，主要指创新能力、问题求解能力、决策能力和批判性思维能力。结合数学学科自身的特点来看，所谓数学高阶思维是指发生在数学思维活动中的较高认知水平层次上的心智活动或认知能力，在教学目标分类中表现为分析、综合、评价和创造，具有严谨性、深刻性、定量性、批判性、独创性、灵活性等特点。

新课程改革以来，新的教学模式不断涌现，例如小组合作学习、分层次教学、网络辅助等。相对于传统教学，这些新的教学模式虽然能够活跃课堂气氛，但对促进学生理解数学本质远远不够，学生的数学思维很难得到锻炼，高阶思维更无从谈起。如果学生的数学高阶思维长期得不到培养，那么他们的学习能力则难以提升。

三、数学核心素养下高阶思维的培养

数学教学不仅要求学生掌握数学知识，更需要培养学生通过学习数学知识来发展高层次的思维能力。培养学生的数学高阶思维能力的最有效方式，就是在课堂教学中让学生运用数学高阶思维进行数学学习，以数学知识为载体分析、综合评价等。

（一）加强数学阅读能力的培养是培养数学高阶思维的有效途径

数学阅读是在理解文字语言的基础上对数学题目进行分析、综合、归纳、推理、猜想等一系列的思维过程。数学语言包含文字语言、符号语言、图形语言，在审题过程中需要用数学的符号语言将信息提取出来，所以数学阅读过程本身就是一种高阶思维的过程。而要提高学生的数学阅读能力，首先要坚定学生的信心，数学题目时而简洁，时而结合实际背景，篇幅较长，学生需要逐字逐句地阅读，还要边阅读边画图，慢慢读懂全题，从而找到解题的关键。其次学会运用阅读技巧，学生需要充分理解题目中的每一个数学符号和数学术语，在理解每一小段的基础上，将问题与已知信息结合起来。阅读数学题目的过程中需要理解、分析、联系、抽象，甚至猜想。因此，培养学生的数学阅读能力的过程也是培养学生数学高阶思维的过程。

案例1：圆的两条不是直径的相交弦不能互相平分。

尽管只有短短的十几个字，但是要解决这道题得先运用原命题与其逆否命题真假性相同理解题意，然后用反证法来证明。

案例2：一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n。如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验;如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验;其他情况下，这批产品都不能通过检验。

假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立。

（1）求这批产品通过检验的概率;

（2）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为x（单位：元），求x的分布列及数学期望。

求离散型随机变量的分布列，内容综合性强，涉及排列、组合、二项式定理和概率，与实际应用联系紧密，所以题目一般字数较多，学生需要耐心读题，读题的过程应是：具体——抽象——具体，即由感性认识上升到理性认识，形成抽象思维，这是一个归纳过程，然后用归纳的结论去指导具体问题的解决，这是一个演绎过程，学生应遵循两个程序，循环往复，循序渐进，深入理解，寻求解决方案。

（二）发散思维之一题多解是培养数学高阶思维的有效手段

教学过程中应有意识地通过一题多解的方式提高学生的思维能力。通过对习题进行多种解答，学生能够充分地了解知识点之间的关联，从不同的角度理解数学知识和方法。一题多解的训练需要教师的启发引导，教师引导学生进行一题多解，引导学生总结出解题的有效方法。在数学的学习过程中，培养学生一题多解的学习习惯，可以提高学生解决难题的能力，在一定程度上提升了学生的学习质量，提高了学习的效率。同时，通过一题多解的学习方式，锻炼了学生的逻辑推理能力，提高了学生对知识的掌握程度，对于高中的学习具有重要的意义。

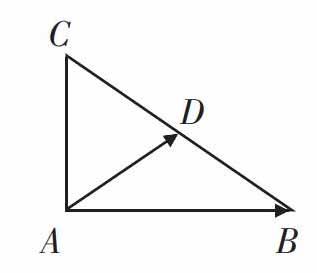
案例3：如图，在Rt△ABC中，∠A=90°，AB=6，点D为BC的中点，则AB·AD= 。

解决此题的方法有：投影法（利用向量的数量积的几何意义）;坐标法（以A为原点建立平面直角坐标系）;基底法（选择以向量AB，AC为基底）;特殊值法（假设△ABC为等腰直角三角形）。

通过这个简单的例子让学生体会一题多解的过程与乐趣，并在平时的习题训练中与学生一起分析、探索、讨论，寻求一题多解，从而在此过程中提高学生的高阶思维。

（三）强化分类讨论思想是培养数学高阶思维的有效手段

加强数学分类讨论思想的训练，有利于提高学生对学习数学的兴趣，培养学生思维的条理性、缜密性、科学性，这种优良的思维品质对学生的未来必将产生深远的影响。教师在教学过程中应有意识地突出分类讨论思想。教学中要遵照循序渐进、逐步深化的原则，并采用灵活多变和有效的教学手段来实施分类讨论方法的教学。我们要多研究、多实践、多探索，让学生更好地掌握好分类讨论思想，这也是实施素质教育的具体表现，数学中的分类讨论教学与素质教育中提出的培养学生的创新精神与探索精神是一致的，同时达到了培养学生高阶思维的目的。

（四）培养学生数学高阶思维应注意的问题

数学核心素养下高阶思维的培养既要时常总结、评价、创新、探究，又要做到深入浅出，不能一味地追求高阶思维的培养，随意增大教学的难度而加重学生的负担，甚至导致部分学生跟不上教学节奏而失去学习数学的兴趣。数学核心素养下高阶思维的根本目的在于引导学生自主学习，积极实践创新，形成和发展数学核心素养。

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2]教育部考試中心.高考文科试题分析[M].北京：高等教育出版社，2017.