一种逆结构滤波法的轨道车辆轮轨力识别

王明猛 朱涛 王小瑞

摘要： 轮轨动态接触力对车辆运行安全性和稳定性至关重要，考虑到在实际运行条件下，轮轨力很难测量的难题，基于离散时间和动力学状态空间方程，提出了一种逆结构滤波的时域载荷识别方法。该方法以结构响应参数为输入，可实现对非最小相、非并置结构的载荷预测，解决了由于非并置逆系统的不稳定性带来的载荷识别困难。以某轨道车辆为研究对象，以轴箱位置加速度为输入条件，分别建立了10自由度的垂向振动模型和17自由度的横向振动模型，对车辆的轮轨垂向载荷和横向载荷进行了识别。识别结果与具有完全相同动力学参数的SIMPACK仿真模型结果对比，结果表明：反演模型识别出的轮轨垂向力和横向力与SIMPACK仿真结果趋势一致，且均有较强的相关性，识别精度较高;通过滚动振动试验台试验，利用一组测得的垂向加速度响应和垂向位移响应对车辆轴箱的加速度响应进行了识别，并与测得的结果进行对比，相关系数达到0.9756，为极强相关，方法能够用于运行列车轮轨力的监测和安全评估。

关键词： 载荷识别; 轨道车辆; 逆结构滤波; 脱轨系数

中图分类号： O313.4; U213.2+12 文献标志码： A 文章编号： 1004-4523（2019）04-0602-07

DOI：10.16385/j.cnki.issn.1004-4523.2019.04.006

引 言

运行条件下车辆的实时轮轨接触力信息对于脱轨预测、轮对磨耗和疲劳的确定、标定轨道上的作用力，甚至列车运行速度的限定等都是非常有用的。然而，在实际运行条件下轮轨接触力是难以用直接测量的办法得到的，采用载荷识别技术，由实测的结构响应来反求结构的载荷便成为一种重要的分析手段。

随着计算机水平的提高和新学科的涌现，载荷识别理论和方法越来越多[1]，识别精度也越来越高，但绝大多数停留在对具有理论解、线性结构、或弱非線性结构上的运用研究上[2]。由于载荷识别技术在间接测量上的独特优势，近年来在轨道车辆上的运用日渐增多，且具备了一定的理论和工程参考价值。T Uhl[3]提出了一种基于测得的系统响应，识别线性范围内的车辆轮轨力的方法，该方法能够得到一定精度的轮轨垂向力，但横向力的识别并不理想。朱涛[4]提出了一种非迭代的载荷识别时域方法，利用车辆结构的加速度响应和位移响应，实现了对车辆垂向接触力的识别，并利用滚动振动试验台测试数据对该方法进行了验证。Zeng等[5]推导出了悬挂轮对的平衡方程，将测量的悬架和惯性力作为输入条件，间接计算轮轨力。Sun等[6]提出了一种基于货车车体、转向架构架、轴箱等加速度响应的轮轨垂向动态载荷的识别方法，同时可以基于该方法得到车辆二系悬挂和一系悬挂载荷。Xia等[7-8]基于集成和部分模态矩阵技术，提出了一种基于测量车体垂向、横向、侧滚、点头和摇头加速度的铁道货车反演模型，对一定速度下的货车轮轨力进行识别，但该方法仅适用于20 Hz以下低频信号的预测。Lars Nordstrm[9]提出了车辆轮轨力的识别方法，但是反演识别模型不是基于车体的加速度，并且不适用于车载、适时系统。这些研究在一定程度上为载荷识别方法在轨道车辆上的运用提供了可行性探索，但是鉴于轨道车辆结构的复杂性，这些方法均具有一定的使用局限性。

本文基于离散时间和动力学状态空间方程，提出了一种逆结构滤波的时域载荷识别方法，以结构响应参数为输入，对非最小相、非并置结构的载荷进行预测。以某轨道车辆为研究对象，对车辆的轮轨垂向载荷和横向载荷进行了识别，并与具有完全相同动力学参数的SIMPACK仿真模型结果对比，从而有效地替代了昂贵的线路试验获取轮轨力的过程，初步实现了对车辆运行安全性的评估。

1 逆结构滤波法的数学模型

利用式（16）求出滤波系数R，即可得到待求解的载荷历程。

基于MATLAB对逆结构滤波法进行程序化，得到以加速度响应为输入，以载荷为输出的程序化计算模块。

2 载荷识别的正则化方法

正则化理论在动载荷反演技术的发展运用中占据着非常重要的地位，正则参数的合理选择是反演结果好坏的最直接影响因素，这是由反问题本身存在的不适定性等客观因素所决定的。在逆结构滤波数学模型的基础上，引入Tikhonov正则化方法，得到正则化参数，可有效抑制识别载荷的漂移现象。

L曲线准则是以lg-lg尺度来描述残差的范数‖hu-y‖22与解的范数‖u‖22之间的曲线对比，该曲线竖直与水平的拐角部位（最大曲率），残差的范数和解的范数取得了折衷，所对应的即为最优正则参数，其名称的由来是基于上述尺度作图时将出现一个明显的L曲线，如图1所示。

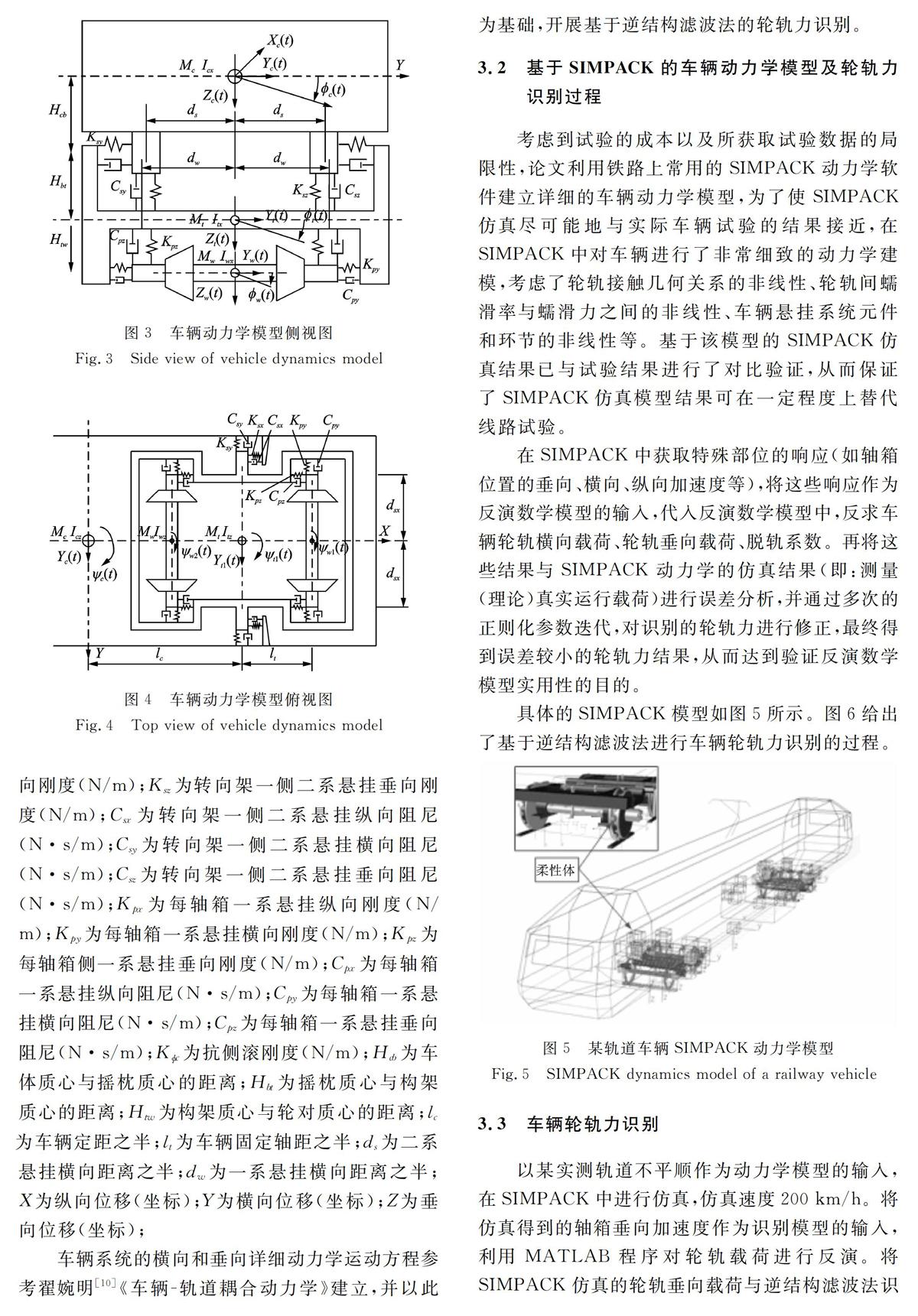
3 轨道车辆轮轨载荷识别〖*3〗3.1 车辆轮轨力识别力学模型  以某两轴轨道车辆为例，系统由7个刚体组成，建立车辆系统垂向运动和横向运动解耦的微分方程，对于车辆垂向响应的研究，只考虑各部分的浮沉、点头及侧滚自由度;对于横向响应的研究，只考虑各部件的横移、摇头和侧滚自由度。车体系统垂向和横向随机振动研究所考虑的自由度，如表1，2所示。车辆动力学模型如图2-4所示。

图2-4中的参数说明：Mc 为车体质量;Mt 为构架质量;Mw 为轮对质量;Iwx为轮对绕X轴转动惯量;Iwy为轮对绕Y轴转动惯量;Iwz为轮对绕Z轴转动惯量;Itx为构架绕X轴转动惯量;Ity为构架绕Y轴转动惯量;Itz为构架绕Z轴转动惯量;Icx为车体绕X轴转动惯量;Icy为车体绕Y轴转动惯量;Icz为车体绕Z轴转动惯量;Ksx为转向架一侧二系悬挂纵向刚度（N/m）;Ksy为转向架一侧二系悬挂横向刚度（N/m）;Ksz为转向架一侧二系悬挂垂向刚度（N/m）;Csx为转向架一侧二系悬挂纵向阻尼（N·s/m）;Csy为转向架一侧二系悬挂横向阻尼（N·s/m）;Csz为转向架一侧二系悬挂垂向阻尼（N·s/m）;Kpx为每轴箱一系悬挂纵向刚度（N/m）;Kpy为每轴箱一系悬挂横向刚度（N/m）;Kpz为每轴箱侧一系悬挂垂向刚度（N/m）;Cpx为每轴箱一系悬挂纵向阻尼（N·s/m）;Cpy为每轴箱一系悬挂横向阻尼（N·s/m）;Cpz为每轴箱一系悬挂垂向阻尼（N·s/m）;Kc为抗侧滚刚度（N/m）;Hcb为车体质心与摇枕质心的距离;Hbt为摇枕质心与构架质心的距离;Htw为构架质心与轮对质心的距离;lc 为车辆定距之半;lt 为车辆固定轴距之半;ds 为二系悬挂横向距离之半;dw 为一系悬挂横向距离之半;X 为纵向位移（坐标）;Y 为横向位移（坐标）;Z 为垂向位移（坐标）;

车辆系统的横向和垂向详细动力学运动方程参考翟婉明[10]《车辆-轨道耦合动力学》建立，并以此为基础，开展基于逆结构滤波法的轮轨力识别。

3.2 基于SIMPACK的车辆动力学模型及轮轨力识别过程  考虑到试验的成本以及所获取试验数据的局限性，论文利用铁路上常用的SIMPACK动力学软件建立详细的车辆动力学模型，为了使SIMPACK仿真尽可能地与实际车辆试验的结果接近，在SIMPACK中对车辆进行了非常细致的动力学建模，考虑了轮轨接触几何关系的非线性、轮轨间蠕滑率与蠕滑力之间的非线性、车辆悬挂系统元件和环节的非线性等。基于该模型的SIMPACK仿真结果已与试验结果进行了对比验证，从而保证了SIMPACK仿真模型结果可在一定程度上替代线路试验。

在SIMPACK中获取特殊部位的响应（如轴箱位置的垂向、横向、纵向加速度等），将这些响应作为反演数学模型的输入，代入反演数学模型中，反求车辆轮轨横向载荷、轮轨垂向载荷、脱轨系数。再将这些结果与SIMPACK动力学的仿真结果（即：测量（理论）真实运行载荷）进行误差分析，并通过多次的正则化参数迭代，对识别的轮轨力进行修正，最终得到误差较小的轮轨力结果，从而达到验证反演数学模型实用性的目的。

具体的SIMPACK模型如图5所示。图6给出了基于逆结构滤波法进行车辆轮轨力识别的过程。

3.3 车辆轮轨力识别

以某实测轨道不平顺作为动力学模型的输入，在SIMPACK中进行仿真，仿真速度200 km/h。将仿真得到的轴箱垂向加速度作为识别模型的输入，利用MATLAB程序对轮轨载荷进行反演。将SIMPACK仿真的轮轨垂向载荷与逆结构滤波法识别的載荷进行对比。图7为L曲线法求得的正则化参数曲线。车辆一位端（前进方向）第一个轮对的轮轨垂向载荷和横向载荷分别如图8，9所示。

将识别结果与SIMPACK模型仿真结果进行对比，通过图8可以看出，识别的轮轨垂向载荷与仿真结果趋势一致，其相关系数为0.82，这说明反演数学模型能够较好地对车辆轮轨垂向载荷进行预测。同样地，通过图9可以发现，反演的轮轨横向载荷与仿真结果趋势基本一致，其相关系数分别为0.75，通过垂向反演结果与横向反演结果的比较，横向反演结果相对较差，这是由于轮轨横向接触具有很强的非线性造成的，但是反演横向载荷的整体趋势还是与仿真结果一致的。

为了体现逆结构滤波法在轨道车辆运行安全性方面的作用，更进一步地对轮对的脱轨系数进行了对比，图10为识别模型的脱轨系数与SIMPACK模型仿真的脱轨系数对比。

通过对车体一位端（前进方向）第一个轮对脱轨系数的比较，可以看出两种方法得到的脱轨系数趋势非常一致，这说明反演数学模型能够较好地对车辆的脱轨系数进行预测，进而能够起到实时监测列车运行安全性的作用。

3.4 车辆轮轨力识别的试验验证

在滚动振动试验台上，利用24通道的DDS32数据采集系统分别对车体垂向加速度、构架的垂向加速度以及4个轴箱垂向加速度和位移进行了采集。试验速度为280 km/h，输入的激励为武-广线实测轨道谱。

由于试验条件的限制，滚动振动试验台的试验无法对车辆的垂向、横向接触力进行直接测量，因此主要是利用一组测得的垂向加速度响应和垂向位移响应对车辆轴箱的加速度响应进行识别，并与测得的结果进行对比，从响应识别的角度对理论模型进行验证。

识别得到的第4个轴箱加速度与测量加速度对比如图11所示，其相关系数达到0.9756，为极强相关，说明基于逆结构滤波法对车辆响应的识别具有很高的识别精度。

4 结 论

论文提出了一种基于逆结构滤波法的动态载荷时域识别方法，并将这种方法运用在轨道车辆轮轨作用载荷的识别当中，通过对轴箱位置加速度的测量，实现了对轮轨力的识别。通过对理论方法的推导和运用，主要得到以下结论：

（1）基于离散时间和动力学状态空间方程的逆结构滤波时域载荷识别方法，可实现对非最小相、非并置结构的载荷预测，解决了非并置逆系统的不稳定性带来的载荷识别困难。

（2）以轨道车辆的轮轨力为识别对象，识别结果与具有完全相同动力学参数的SIMPACK仿真模型结果对比，表明逆结构滤波的载荷识别方法对轨道车辆的轮轨接触载荷的识别具有比较高的精度，运用本方法可以初步实现列车轮轨力的预测的运行安全性的评估。

由于试验条件的限制，理论模型仅通过识别的轴箱加速度与实测的加速度进行了对比，下一步将通过实测的轮轨力对比证明模型的准确性;另外，模型仅实现了线性范围内轮轨接触载荷的识别，由于轮轨接触具有一定的非线性因素，下一步将进一步完善识别数学模型，以得到更准确的载荷识别结果。

参考文献：

[1] 马富银， 吴九汇， 吴伟蔚. 修正载荷识别远场误差的虚拟远场激励方法[J]. 机械工程学报， 2016，52（1）：116-122.

MA Fuyin， WU Jiuhui， WU Weiwei. Improving the far-field errors for load identification based on virtual far-field exciting method[J]. Journal of Mechanical Engineering， 2016，52（1）：116-122.

[2] Xingsheng Sun， Jie Liu， Xu Han， et al. A new improved regularization method for dynamic load identification[J]. Inverse Problems in Science and Engineering， 2014，22（7）： 1062-1076.