执行器失效的线性系统输入输出有限时间稳定
2019-10-21吴保卫
甘 艺,吴保卫
(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)
0 引 言
在实际的控制系统中, 由于一些环境因素的影响, 控制元件发生故障是不可避免的, 如控制器失效, 执行器失效等。 控制元件失效会导致整个系统不稳定甚至性能恶化。 因此, 在控制元件失效的情况下,研究整个闭环系统的稳定性引起了广泛关注[1-3]。稳定性是系统的重要性能之一,指数稳定和 Lyapunov 稳定反映了在无限时间间隔内系统逐渐趋于零的行为, 而有限时间稳定 (FTS) 和输入输出有限时间稳定 (IO-FTS) 则反映了在有限或者较短时间间隔内的系统行为。实际应用中, 有时只需要系统在有限时间区间内的暂态性能,研究系统的输入输出有限时间稳定就非常必要[4-10]。 文献 [4] 介绍了线性系统的输入输出有限时间稳定的概念;文献 [5-6]分别研究了奇异时变系统和脉冲系统的输入输出有限时间稳定; 文献 [7-9] 研究了分数阶切换系统的输入输出有限时间稳定;文献 [10] 对具有时变和扰动延迟的正切换系统的输入输出有限时间稳定进行了研究。
切换系统[11-12]是由若干连续时间子系统或离散时间子系统及作用在其中的切换规则构成的混杂系统。 即使一部分或者所有的子系统都不稳定, 通过设计合适的切换规则, 可使得整个系统保持稳定。 因此, 切换系统分析与设计在化工过程[13]、 电力系统[14]、 网络控制系统[15]及近空间飞行器控制系统[16]等得到了广泛应用。 文献 [17] 研究了在平均驻留时间下切换系统的输入输出状态稳定特性; 文献 [18] 在事件触发基础上研究了具有异步切换的网络线性切换系统的有限时间稳定; 文献 [19] 研究了脉冲切换系统的有限时间稳定; 文献 [20] 研究了基于事件触发的不确定时滞切换系统的有限时间稳定; 文献 [21] 在事件触发下对切换奇异系统的输入输出有限时间稳定进行了研究。 但是目前还没有基于执行器失效的线性系统的输入输出有限时间稳定的结果; 鉴于此, 本文讨论在执行器失效的情况下线性系统的输入输出有限时间稳定。 首先, 给出了基于执行器失效的系统不可用率的概念。 然后, 通过系统不可用率并且利用平均驻留时间和 Lyapunov 方法,得到输入输出有限时间稳定的可解条件。 相较于文献[1-2], 本文主要考虑系统在有限时间内的暂态性能, 这些条件比文献[4]中给出的条件保守且适用范围更广。 文献[4]只讨论了最基本的线性系统的输入输出有限时间稳定。 此外, 文献[4]中的系统可以作为特例包含于本文所考虑的系统中。 文中,Rn表示n维欧式向量空间,Rn×m表示所有的n×m维的实矩阵; 对于矩阵P,P>0 表示P是正定矩阵,PT是矩阵P的转置,P-1是矩阵P的逆。
1 问题陈述和预备知识
考虑线性系统
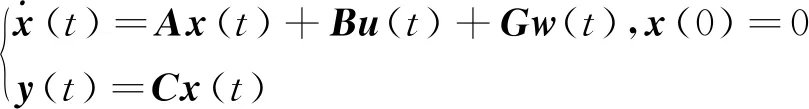
(1)
式中:x(t)∈Rn,u(t)∈Rp,y(t)∈Rq是系统状态, 控制输入和测量输出;A,B,C,G是适当维数的实矩阵;w(t)∈Rm是连续的外部干扰, 并且满足

(2)
式中:T表示有限时间;S表示正定矩阵;d表示一个正常数。

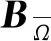
假设在一段时间内, 执行器在ω内失效并且需要一段时间恢复。因此, 系统(1)的状态可以写成如下分段微分方程:
(3)
对于系统(1)设计状态反馈控制器u(t)=Kσ(t)x(t)=Lσ(t)Qσ(t)x(t), 将u(t)代入系统(1)得到对应的闭环系统
(4)
因此,系统(4)可以简化为下面的切换系统
(5)

定义1[11]对于任意的切换信号σ(t)和t2≥t1>0,令Nσ(t)(t1,t2)是时间间隔 (t1,t2)内σ(t)的切换次数。若存在正数N0和τa使得
(6)
式中:τa称为平均驻留时间;N0称为抖振界。 为方便起见, 文中选取N0=0。
定义3[7]系统 (1) 关于(R,P,T)输入输出有限时间稳定, 若对于给定的切换信号σ(t),有
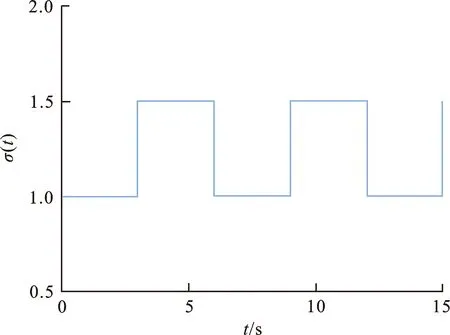
yT(t)Py(t) (7) 式中:R是一类定义在[0,T]上的输入信号;P>0,T>0,c>0。 针对闭环系统(4),讨论系统输入输出有限时间稳定的充分条件。 定理1对于给定的 (R,P,T),∀t∈[0,T],若存在非奇异矩阵Qi>0 (i=1, 2),S>0及实数α>0,β>0,μ>0, 使得下列条件成立: (8) (9) Q1≤μQ2 (10) Q2≤μexp((α+β)T)Q1 (11) (12) 并且切换信号满足 (H1) 不稳定率 (H2) 平均驻留时间 则闭环系统(4)是输入输出有限时间稳定的。 证明当t∈[t2k,t2k+1)时,构造如下形式的Lyapunov函数: V1(t)=xT(t)Q1x(t) (13) 对V1(t)关于t求导,得 (14) 式中 ξ(t)=[xT(t)wT(t)]T (15) (16) (17) 因此 (18) 从t2k到t积分可得 V1(t)≤exp(-α(t-t2k))V(t2k)+ (19) 同理,当t∈[t2k+1,t2k+2) 时, 构造Lyapunov函数: V2(t)=xT(t)Q2x(t) (20) 对V2(t)关于t求导得 (21) 式中 (22) (23) 因此 (24) 从t2k+1到t积分可得 (25) 不失一般性, 假设执行器在 [t2j,t2j+1) 工作, 在 [t2j+1,t2j+2) 失效, 其中j=1,2,…。定义如下形式的Lyapunov函数: V(t)=Vσ(t)(t),σ(t)=1,2 其中,Vσ(t)(t)=xT(t)Qσ(t)x(t)。假设V1(t) 在[t2j,t2j+1)是被激活的,V2(t)在[t2j+1,t2j+2) 是被激活的,j=1,2,…。那么,∀t>0,有 (26) 由式(9),(10)和(25),当t∈[t2k,t2k+1)时,有 (27) 式中 同理,当t∈[t2k+1,t2k+2)时,有 (28) 所以,对于t∈[t2k,t2k+2),有 (29) 在零初始条件下, 结合(H1),(H2), 式(28)等价于 (30) 由于平均驻留时间满足(H2),式(30)等价于 V(t)=xT(t)Qσ(t)x(t) (31) 再由式(11)可得 yT(t)Pσ(t)y(t)=xT(t)CTPσ(t)Cx(t)≤ xT(t)Qσ(t)x(t) (32) 因此,闭环系统(4)是输入输出有限时间稳定的。定理1得证。 通过数值算例验证所提出的控制器设计方法和输入输出有限时间稳定的有效性。 例1考虑线性系统(1),参数如下: 由于执行器失效,系统(1)可以化为闭环系统(4),其中, 为进一步证明本文设计方法的有效性,分别给出执行器不失效及失效下yT(t)Py(t)的仿真结果,如图1~2所示。同时给出切换信号的仿真结果,如图3所示。 图 1 执行器不失效yT(t)Py(t)的状态轨迹图Fig.1 The trajectory of yT(t)Py(t) without actuator failures 图 2 执行器失效yT(t)Py(t)的状态轨迹图Fig.2 The trajectory of yT(t)Py(t) with actuator failures 图 3 切换信号σ(t)Fig.3 The switching signal σ(t) 例2考虑具有外部扰动的机械旋转切削过程的可靠控制问题[22],选择如下系数矩阵: 由于执行器失效, 系统可以化为闭环系统, 其中, 执行器不失效和执行器失效下yT(t)Py(t)的仿真结果如图4~5所示。切换信号的仿真结果如图6所示。 图 4 执行器不失效yT(t)Py(t)的状态轨迹图Fig.4 The trajectory of yT(t)Py(t) without actuator failures 图 5 执行器失效yT(t)Py(t)的状态轨迹图Fig.5 The trajectory of yT(t)Py(t) with actuator failures 图 6 切换信号σ(t)Fig.6 The switching signal σ(t) 讨论了在执行器失效的情况下线性系统的输入输出有限时间稳定问题。 基于切换的方法, 通过设计状态反馈控制器,保证了在执行器失效的情况下系统的输入输出有限时间稳定性, 同时也得到了状态输出反馈控制器的系数矩阵。后续将围绕时滞奇异系统和不确定奇异系统在执行器失效下的输入输出有限时间稳定展开讨论。2 主要结论

3 数值算例

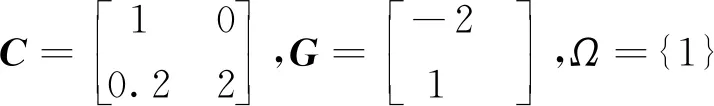
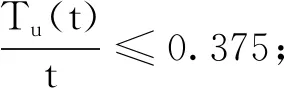


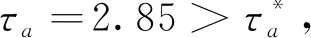

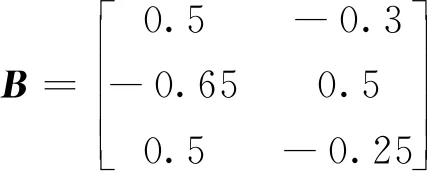




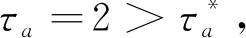

4 结 语
