一组关于Fibonacci数列及Lucas数列的恒等式
2019-10-21陈国慧
陈国慧
(海南师范大学 数学与统计学院, 海南 海口 571158)
0 引 言
二阶线性递推数列和式的计算问题在数学的理论学习及科研应用中占有十分重要的位置,引发了不少数学家的重视和兴趣,并取得了很多有意义的研究成果[1-4]。其中,Fibonacci数列和Lucas数列在一些著名数论问题的研究中有着重要的应用,有关其各类性质的研究也是近年的热点问题[5-6]。Duncan[7]和Kuipers[8]研究了关于Fibonacci数的均匀分布及其应用;Zhang等[9-10]研究了Fibonacci多项式的性质,并证明了一系列包含Fibonacci多项式,Fibonacci数及Lucas数的恒等式。Ma等[11]利用xn所定义的Chebyshev 多项式的表达式给出了Fibonacci数和Lucas数的相关恒等式。Wang等[12]探讨了Fibonacci多项式及Lucas多形式的幂和,获得了不少有趣的等式,并用所得结果对Melham所提出猜想[13]的验证做了进一步推进。其他关于Fibonacci的研究结果参见文献[14-16]。Chen[17],LYU[18-19],Wang[20]及Song[21]等关于Chebyshev多项式及其应用也给出了众多结果。

这就是著名的Fibonacci数列及Lucas数列。

Xn=Ln(x)=αn(x)+βn(x)
分别为Fibonacci多项式及Lucas多项式。
本文主要讨论对和式
(1)
的计算问题, 其中k∈N+,n∈N,求和号表示对所有满足方程a1+a2+…+ak=n的非负整数组 (a1,a2,…,ak)求和。
关于式(1)的求和问题,尚未见到研究,主要原因可能在于这类数列的生成函数中没有阶乘,因而只考虑不带阶乘的其他形式。事实上如果A=B=1, 那么这类数列的生成函数形式非常简单,即
然而,随着Xn取值的变化,式(1)包含一系列不同形式的数列或多项式。从而,可以获得许多数列或多项式的新的恒等式。因此,式(1)的计算问题是有意义的。
1 主要结果
利用初等方法以及指数函数的幂级数展开的唯一性研究了式(1)的计算问题,并给出具体的计算公式。为方便阐述,假定在Xn表达式中取A=B=1,则有如下的结果:
定理1设n∈N+,对任意正奇整数k, 有恒等式
定理2设n∈N+,对任意偶数2h, 有恒等式

可以推出关于Lucas数的恒等式:
推论1设n∈N+,对任意正奇整数k及m∈N+, 有恒等式
推论2设n∈N+,对任意正偶数k及m∈N+, 有恒等式
推论3设n∈N+,对任意正奇整数k及m∈N+, 有恒等式
推论4设n∈N+,对任意正偶数k=2h及m∈N+, 有恒等式
特别当k=3,m=1时,注意到L1=1及T1(x)=2x, 有如下推论:
推论5∀n∈N+,有恒等式
推论6∀n∈N+,有恒等式
当h=2,m=1时,注意到L1=1及T1(x)=2x, 得到下述推论:
推论7∀n∈N+,有恒等式
推论8∀n∈N+,有恒等式
2 定理的证明
2.1定理1的证明
由二项式定理可知,当k为奇数时,有
(2)
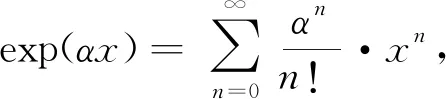
(3)
另一方面,注意到恒等式
则有
(4)
应用式(3)及式(4)并比较幂级数的系数可得
于是定理1得证。
2.2 定理2的证明
如果k是偶数,不妨设k=2h, 那么由二项式定理有恒等式
(5)
应用式(5)以及定理1的证明方法,易推出恒等式
于是定理2得证。
