一类Baouendi-Grushin方程解的对称性

钱红丽,黄小涛

(南京航空航天大学 理学院,江苏 南京 211106)

1 引言及主要结论

二阶椭圆偏微分方程解的存在唯一性、正则性和对称性等性质是偏微分理论研究的主要内容。关于解的对称性和单调性,现已有的研究成果很多。不仅方程所在的各种区域被研究,比如有界区域、外部区域、环形区域和全空间Rn等。各类方程也被充分研究,比如Laplace方程、p-Laplace方程、各类退化椭圆方程、位势积分方程以及分数阶偏微分方程等。主要研究方法包括移动平面法、移动球面法、Hardy-Littlewood-Sobolev不等式、Leray-Shauder定理、不动点定理、变分法和重排等。

经过近几十年的发展,二阶线性椭圆方程的基础理论已经比较完善[1-2]。关于完全非线性偏微分方程解的存在性、正则性等理论,经过Caffarelli[3]等的研究,已经成一定体系。但是，关于退化椭圆方程的理论研究,由于退化类型的多样化,目前还没有统一的研究方法和结论。Dibenedetto[4]和Hörmander[5]等研究了退化椭圆方程弱解的正则性等相关性质。近年来,众多学者研究了一类特殊的退化椭圆Baouendi-Grushin方程

ΔGu(z)=f(z),z∈RN

(1)

令z=(x,y)∈Rn×Rm=RN,γ≥0,Baouendi-Grushin型梯度G[6]定义为

则Laplace型Baouendi-Grushin算子可写为

(2)

式中Δx和Δy分别表示Rn和Rm上的Laplace算子。故Baouendi-Grushin方程可写为

Δxu+|x|2γΔyu=f(x,y)

(3)

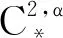
-(Δxu+|x|2γΔyu)=uq

(4)

解的对称性,但是对于更一般的Baouendi-Grushin方程

-ΔGu+m1u=λ|u|q-1u(λ>0,m1>0)

(5)

由于项m1u的存在,移动球面法在此并不适用。 据作者所知,目前还没有方程(5)的对称性结论。

偏微分方程解的存在性和对称性问题可追溯到上世纪50年代。Alexandroff[11]首先研究了二阶偏微分方程解的对称性问题;1971年,Serrin[12]利用移动平面法,研究Laplace方程在有界区域上的对称性及方程解u的特定对称形式;Gidas等[13], Caffarelli等[14]众多学者运用多种形式的极大值原理对移动平面法进行了发展和完善。

本文通过研究一类带约束的极小泛函和重排的方法研究方程(5)解的对称性问题。Berestycki等[15]首先利用此方法来研究Schrödinger型Laplace方程

-Δu+m1u=λ|u|q-1u

得到了方程解的存在性、对称性以及某些特殊情况下解的具体形式等相关结论。事实上，此方程可以看做本文研究的方程(5)当γ=0的情形。

2013年,Dipierro等[16]研究了分数阶Laplace方程，利用约束极小化方法和重排理论,证明了弱解的存在性和对称性。最近,文献[17]研究了分数阶p-Laplace方程

证明了方程存在弱解u∈Ws,p(Rn)满足径向对称性与单调性。

本文利用重排和极小化约束方法研究方程(5)。在此，需定义一类Sobolev空间

具体将在2.1节介绍。为讨论方程(5)正解的存在性和对称性问题,首先将问题转化为如下约束最小化泛函,此方法的主要思想可文献参考[15]。

A(v)=1}

(6)

其中

g(u)=λ|u|q-m1|u|

本文将证明下述结论:

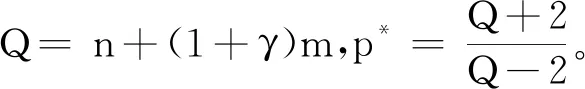
2 预备知识

首先给出一些已知结论和预备知识。文中记Q=n+(1+γ)m,N=n+m。

2.1 内在度量和Sobolev空间

∀z=(x,y)∈Rn×Rm，关于方程(5),定义Carnot-Caratheodory距离[9]为

在空间S1,2(RN)中，若赋予内积

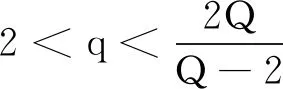
S1,2(Ω)→L2(Ω)

引理1[15]若P,Q:R→R为两个连续函数,满足

设un:RN→R为可测函数序列,则

并且在RN中,当n→+∞时,有

P(un(z))→v(z)

于是对任意Borel集，有

2.2 Schwarz重排

本节回顾Schwarz重排的一些基本性质。如果Ω是RN中的一个开集,并且u:Ω→R为度量函数,定义

μu(t)=|z∈RN:|u(z)|>t|

u*(s)=sup{t≥0:μu(t)≥s}

则u*(z)=u*(ωN|z|N)是u的Schwarz重排,满足径向对称性且关于|z|递减。具体可以参考文献[15，20]。

Schwarz重排具有以下基本性质:

引理2(1) 设v,w为RN中的可积函数,令g:RN→R为单调不减的非负函数,则

(2) 若f,g∈L2(RN),则

‖f*-g*‖L2(RN)≤‖f-g‖L2(RN)

3 定理的证明

首先给出方程(5)常见的拉格朗日函数,即

(7)

为寻找方程(5)的解,可以将问题转化为讨论约束最小化问题(6)。假设u是问题(6)的一个解,则存在拉格朗日乘子θ,使得

-ΔGu=θg(u),z∈RN

(8)

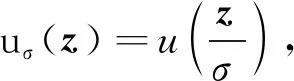
证明问题(6)存在径向对称的正解，由此可推导得到方程(5)解的对称性。定理1的证明分为以下几步。

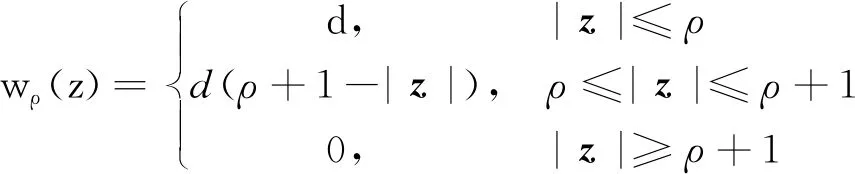
(9)

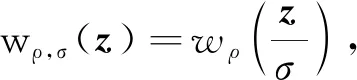
A(v)=1}=I>0

A(v)=1}=I>0

‖uk‖Lp*(RN)≤C‖Guk‖L2(RN)≤C

下面定义

g1(t)=λ|t|q,g2(t)=m1|t|,

将不等式两边从0到u积分,得

结合条件A(uk)=1,有

则|u(z)|

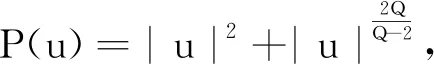
(10)

4 结 语

研究证明了一类退化椭圆型Baouendi-Grushin方程解的对称性问题。由于此退化椭圆方程尚无极值原理,所以无法利用移动平面给出方程解的对称性。利用Schwarz重排研究方程所对应的带约束极小化泛函，是一种切实可行的证明对称性的方法。 通过Sobolev嵌入定理及解的先验估计,证明了方程对应的带约束条件的极小化泛函问题的正解满足Schwarz重排的性质,从而利用Schwarz重排的对称性得到了Baouendi-Grushin方程解的存在性和对称性。