步行荷载的两阶段遗传算法识别

王鹏程， 陈 隽，2， 王浩祺

(1.同济大学 土木工程学院，上海 200092； 2.土木工程防灾国家重点实验室，上海 200092； 3.东京大学 桥梁与结构实验室，东京 113-8656)

随着结构工程的发展，高强度轻质材料在新建建筑中得到了广泛的使用，这使得越来越多的大跨楼盖、人行桥、体育看台等低频、轻质、小阻尼结构出现了明显的人致结构振动问题：人致激励引起的结构的振动过大会引起结构上人群的不适甚至恐慌，严重时甚至会影响工程结构的安全性[1]。

可靠的步行荷载模型是人致结构振动分析的前提。自20世纪70年代以来，很多学者通过固定测力板、测力鞋垫以及动作捕捉等实验方法，实测行人的步行荷载时程，提出了许多步行荷载的数学模型。Galbraith等[2]利用测力板数据，指出荷载曲线具有脚跟着地和脚尖离地的双峰值特性；Ellingwood等[3]采用行走过程中左右脚落足曲线相同的假设，构造出单人步行荷载傅里叶时程曲线；Bachmann等[4]由实测数据得出了步行荷载的竖向前5阶动载因子。Zivanovic等[5]在大量单人步行荷载实测数据的基础上，把步频、步长、荷载幅值视作正态分布，综合主谐波及次谐波的峰值左右附近一定宽度的频谱信息，拟合得出每阶主谐波及次谐波的名义幅值表达式，建立了步行荷载的随机模型;陈隽等[6]将三维动作捕捉技术与测力板相结合，将单步荷载实测值拓展为连续步行荷载，进而建立步行荷载的数学模型。

上述研究成果加强了人们对步行荷载特性的理解，并广泛用于步行荷载下工程结构的振动分析。然而，随着研究和应用的深入，基于刚性地面上实测数据的传统荷载建模的方式也表现出一些问题：受实验空间、测试者对测力板的“对准心理”、设备性能的限制等，无法全面反映测试者的真实步态；对于存在人结相互作用(Human-Structure-Interaction, HSI)的场合,刚性地面所得的荷载模型与实际荷载差异如何等。荷载建模的最终目的是准确计算结构响应。因此，针对上述问题并受车辆移动荷载识别方法的启发，在前期由结构响应反演步行荷载时程的探索研究基础上[7]，本文研究利用遗传算法由结构响应识别步行荷载模型参数，并分别利用步行荷载的数学模型和实测记录分别对方法的准确性及适用性进行了检验。

1 步行荷载的识别方法

1.1 单人步行荷载模型

步行荷载是人致结构振动问题中最重要的荷载形式。步行荷载是空间移动的连续性接触荷载，可引起人行桥等长线性结构的竖向和水平振动。考虑左右脚荷载一致的情况，即步行过程可以看作成以一单步为基础的周期性过程，则竖向的连续步行荷载可以表达为傅里叶级数的形式[8]

(1)

式中:Fv(t)为竖向力；G为人的静止重力；αvi为竖向第i阶傅里叶系数，又称动载因子(Dynamic Loading Factor,DLF)；fp为行人的步行频率；φvi为竖向第i阶谐波相位角；n为模型阶数。

模型阶数的选择应平衡荷载时程的准确表达以及未知参数的个数。参考已有研究成果，阶数取为n=5。

除了作用力外，步行频率也是步行荷载的一个重要指标。步行频率即单位时间内的单步数，例如1.5 Hz表示1分钟内走90步，步行荷载的频率范围大致在1.0～2.5 Hz[9]。

1.2 步行荷载下的结构响应

以一跨度为L的简支梁为例，考虑其多阶振型的影响，用广义单自由度体系方法计算步行荷载作用下的结构位移响应。其简化模型如图1所示。

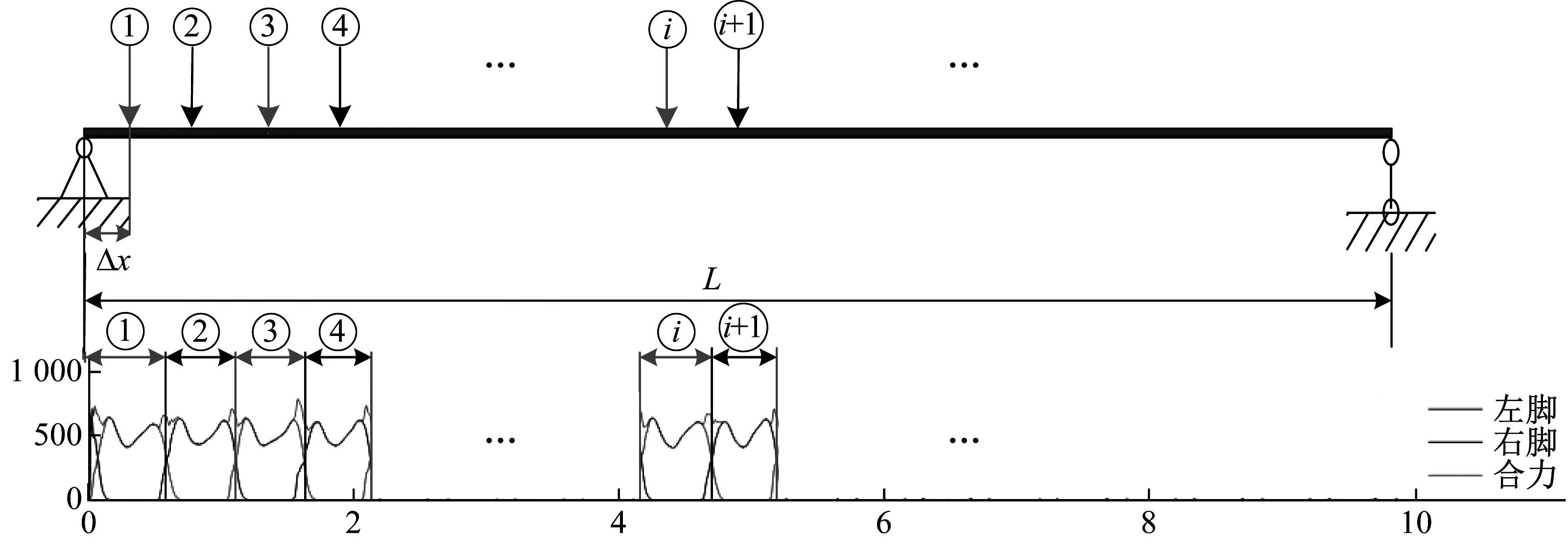
图1 步行荷载作用在简支梁桥上的简化模型

简支梁第i阶振型的广义动力学方程为

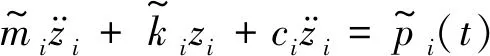
(2)

假设其第i阶振型函数为

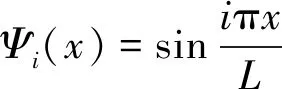
(3)

考虑左右脚位移的影响，确定步行荷载产生的广义力为

(4)

A(t)=(nt+1)×v/fp+Δx

(5)

式中:Fv(t)为竖向的连续步行荷载时程曲线，nt为t时间内最大的单步数，nt=[t×fp]；v为步行速度；Δx为起步点至桥支座的水平距离。

在跨中x=L/2处，其总挠度为[10]

(6)

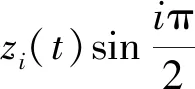
已有研究和工程经验表明，振型越高，对结构响应贡献越小。而叠加的参振振型过多，会影响计算效率。为简化计算，本文所计算的结构响应是结构前4阶跨中位移响应的叠加。

1.3 荷载参数的遗传算法识别

需识别的荷载参数包括傅里叶级数的前五阶动载因子及其相位、步行频率fp等11个参数，行人的步行速度v和结构的位移反应时程u作为已知量。识别分为两个阶段进行：第一阶段确定动载因子和步行频率；第二阶段确定相位。每阶段的识别均采用遗传算法实现。

遗传算法(GA)是一类借鉴生物进化过程的全局优化搜索算法，模拟了自然选择和遗传中发生繁殖、交配和突变现象，从任一初始种群出发，通过随机选择、交叉和变异操作，最终生成符合优化目标的新个体。因其简单通用、鲁棒性强、适于并行计算及应用范围广等特点，广泛用于各类识别问题。

根据以上特点，参考相关GA算例的运算流程[11]，步行荷载识别的具体实现过程可分解为如下六个步骤：

步骤1 编码：即将11个参数转换为二进制形式。假设每个参数二进制位数为20，将参数转化后的二进制数依次排列。两阶段分别形成20×6=120、20×5=100个字符长度的字符串，对应的参数取值范围如表1所示。

表1 待识别参数的取值范围

步骤2 初始种群的生成：随机产生一定数目的个体产生种群，即生成一定数目的字符串(参数组合)。本文中，种群大小皆设置为200。

步骤3 适应度评估：适应度表明个体的优劣性。不同的问题有着不同的适应性函数定义。适应度函数的大小与目标函数有关。两个阶段的目标函数分别为式(7)和式(8)所示。由于目标函数取最小值为最优解，故在本文中适应度函数为目标函数的倒数。

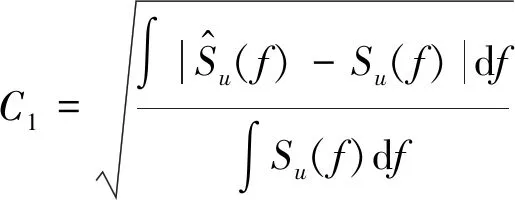
(7)

(8)

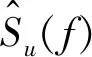
步骤4 选择：选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。常用的选择方法有轮盘赌选择法和随机遍历抽样法，本文采用随机遍历抽样法。

步骤5 交叉：交叉操作是遗传算法中最主要的遗传操作。通过交叉，遗传算法的搜索能力得以飞跃提高。本文采用单点交叉法，交叉概率为90%。

步骤6 变异：变异的基本内容是群体中的个体串的某些基因值的依概率随机变动。通常发生变异的概率很低,取值很小，本文为1%。

地桃花(Urena lobata L.)为锦葵科(Malvaceae)梵天花属(Urena L.)植物[10]，是一种多年生亚灌木状的直立草本，具有祛风利湿、活血消肿、清热解毒的功效。我国长江以南地区均有地桃花分布。目前，对其化学成分分析和药用价值等研究较多[11-14]。在野外调查中发现，地桃花和紫茎泽兰可以共生，并表现出一定的竞争优势，但地桃花提取物除草活性方面的研究鲜见报道。为全面了解地桃花提取物的除草活性，本研究在室内测定了地桃花提取物对10种植物幼苗生长的抑制作用，为这一植物源除草剂资源的开发利用提供依据。

算法采用谢菲尔德大学开发的GA工具箱实现[12]，以上步骤皆可通过工具箱的内置函数来调整参数，其参数配置汇总到表2中。

表2 遗传算法参数配置

2 步行荷载模型的参数识别

2.1 结构模型的基本信息

考虑如图2所示简支梁桥，梁桥的长度L=20 m，线密度为ρ=60 kg/m，EI=3.6×107N·m2，前4阶阻尼比均为ζ=0.02，前4阶基频分别为3.04 Hz、12.17 Hz、27.38 Hz和48.67 Hz。假设单人在该梁上行走，行人的体重为700 N,行走步距为0.75 m，步行频率为2.0 Hz,步行速度为1.25 m/s。假定行走的第一步踩在距左端支座的0.5 m处。桥响应的测量点为跨中0.5L处。

(a) 连续步行荷载时程

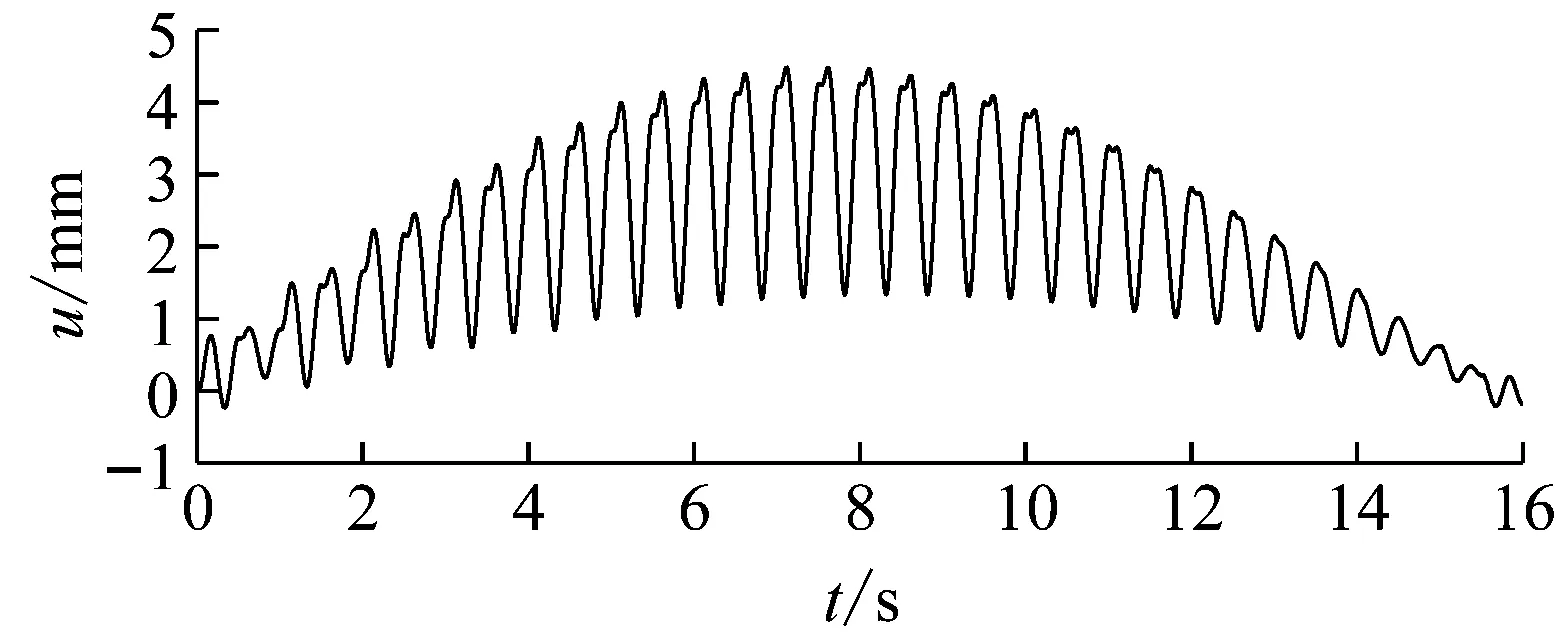
(b) 跨中位移响应时程

对于步行荷载的施加，算例采用陈隽等[13]提出的单人连续步行荷载傅里叶级数模型，其动载因子和相位的数值如表3所示。

荷载模型参数的识别方法及识别过程已经在前一节详细描述。

2.2 识别结果

为评价两阶段识别方法在识别精度和效率上的优劣，同时进行了一次识别全部参数的GA计算，称为一次识别法。为了检验算法的稳定性，避免出现局部收敛现象，将遗传算法重复运行三次，最优的参数集是基于目标函数最小值的原则选定的。表4中显示了系数的识别结果对比；表5是对两种算法运算效率的对比；图3、图4则由荷载时程、傅立叶谱及结构响应时程等方面进行了对比。

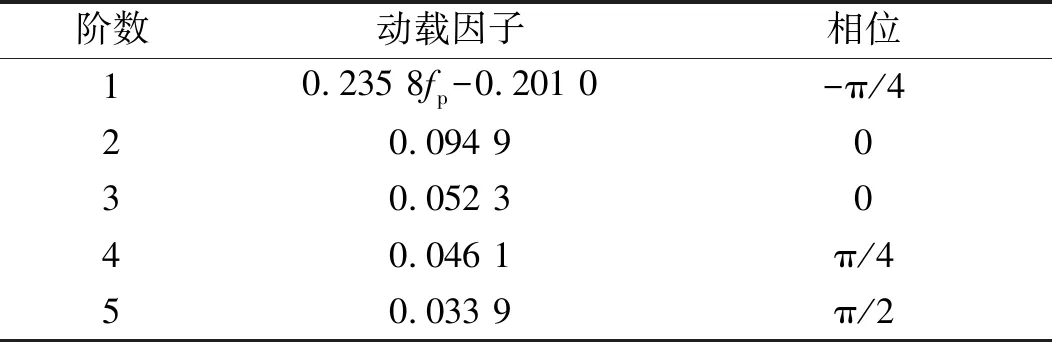
表3 傅里叶级数模型的动载因子和相位

表4 识别结果对比

表5 算法效率对比

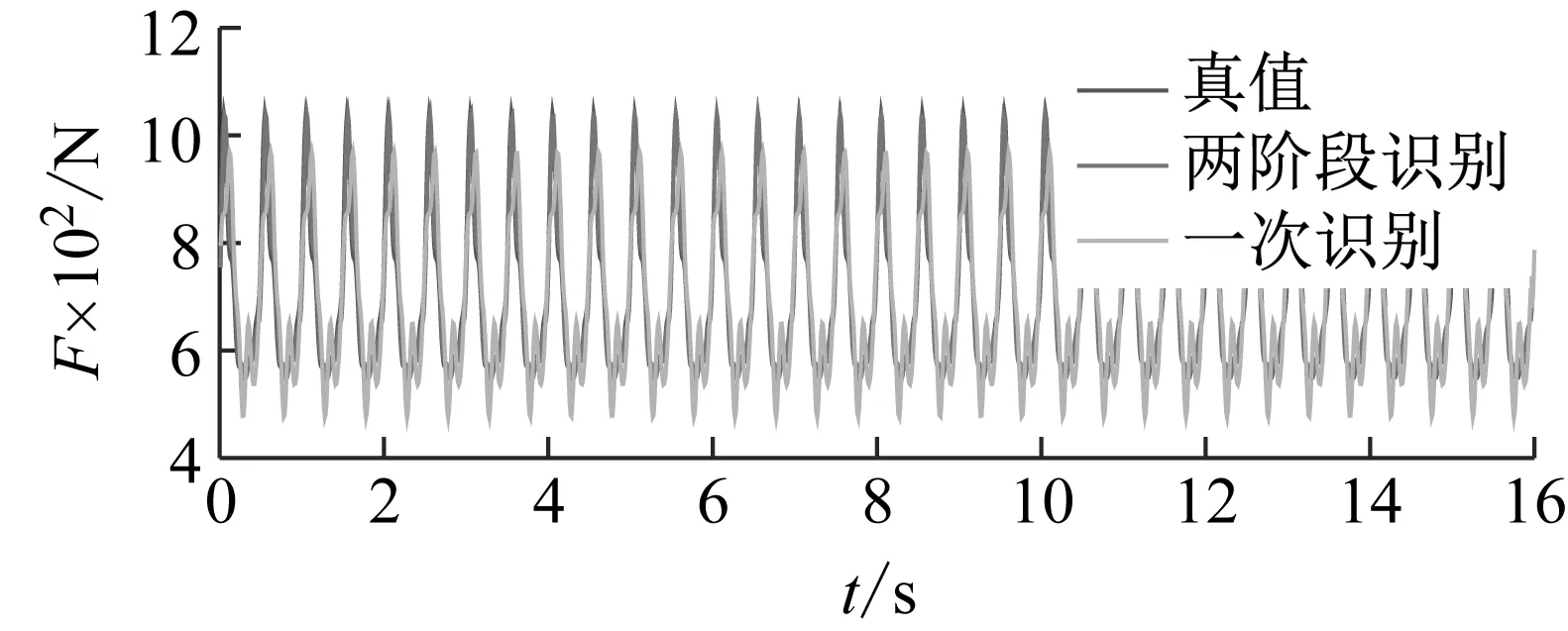
(a) 连续步行荷载时程

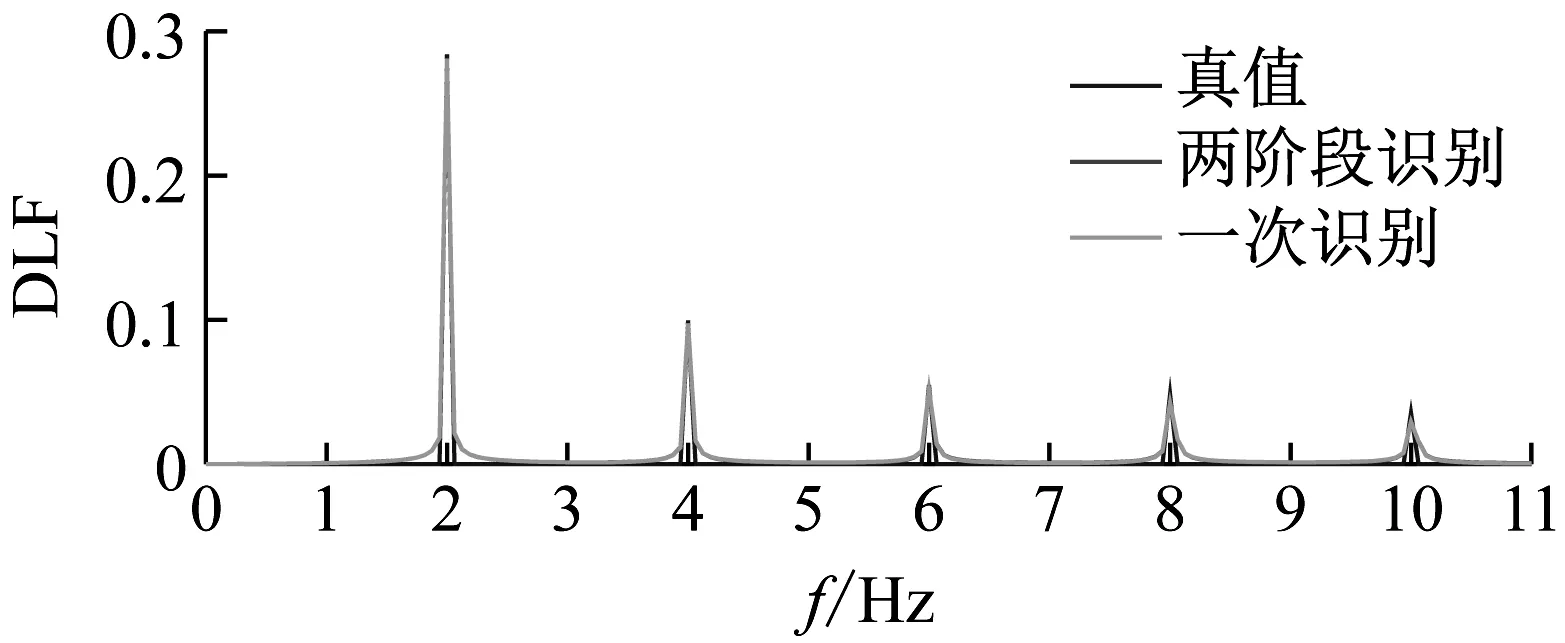
(b) 傅里叶幅值谱

从表4中可以看出，两种方法对于动载因子和步频的识别结果一致，识别误差均在允许范围之内，三条曲线在傅里叶幅值谱中的对比近乎一致，但相位识别精度一般。

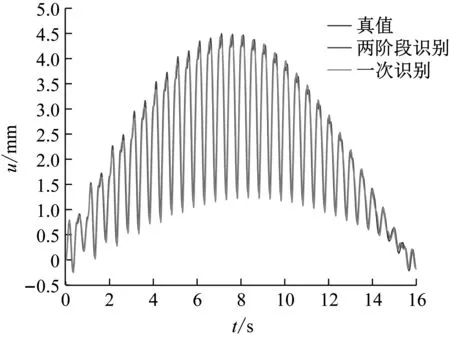
图4 位移响应时程对比

从图3和图4中可以看出，两种方法相位识别结果的不同造成了荷载曲线明显的差异。其中，两阶段方法的结果在荷载时程曲线及结构位移响应方面与真值更为接近。从表5的对比可以得出，两阶段方法的计算效率较一次识别法提高50%以上。在进行重复多次识别后发现，两种方法的动载因子及步频识别结果皆表现稳定；对于相位的识别结果，两阶段方法表现稳定，但一次识别法相对离散(表6)。其原因可能是一次识别法的参数过多，导致其编码长度过长，使算法的计算效率降低，增加了局部收敛的概率。综合以上因素，推荐采用两阶段识别方法进行步行荷载参数的识别。

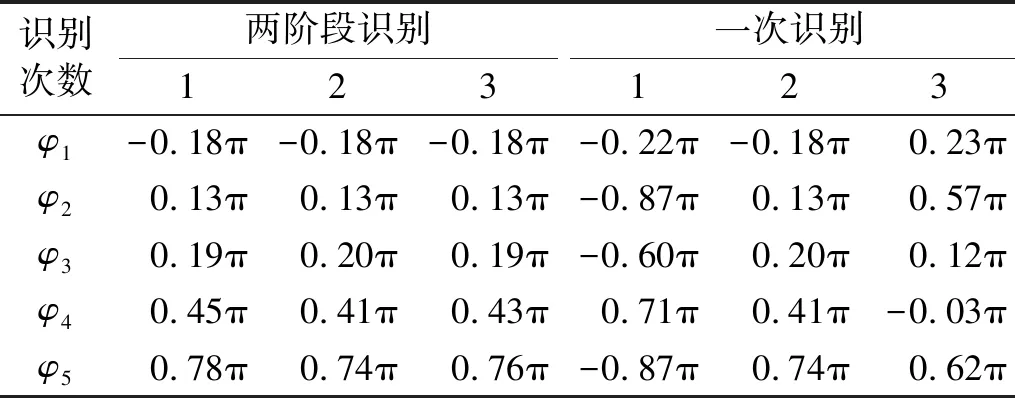
表6 多次相位识别结果对比

3 实测荷载的识别

3.1 实测步行荷载数据来源

本节采用的9条不同步频的步行荷载时程数据皆来自于测力跑步机获得的测量结果。测试者为女性，身高160 cm，体重558 N。采样时间间隔为0.005 s。对实验数据进行统计，得到如表7所示的实验信息。

在实验中，测量过程难免会受到白噪声的影响。为抑制和防止白噪声的干扰，需要对步行荷载的时程数据进行滤波处理。采用butter滤波器，滤波阶数为5阶，截止频率为Wn=2×20/200。处理后的荷载时程曲线如图5所示。

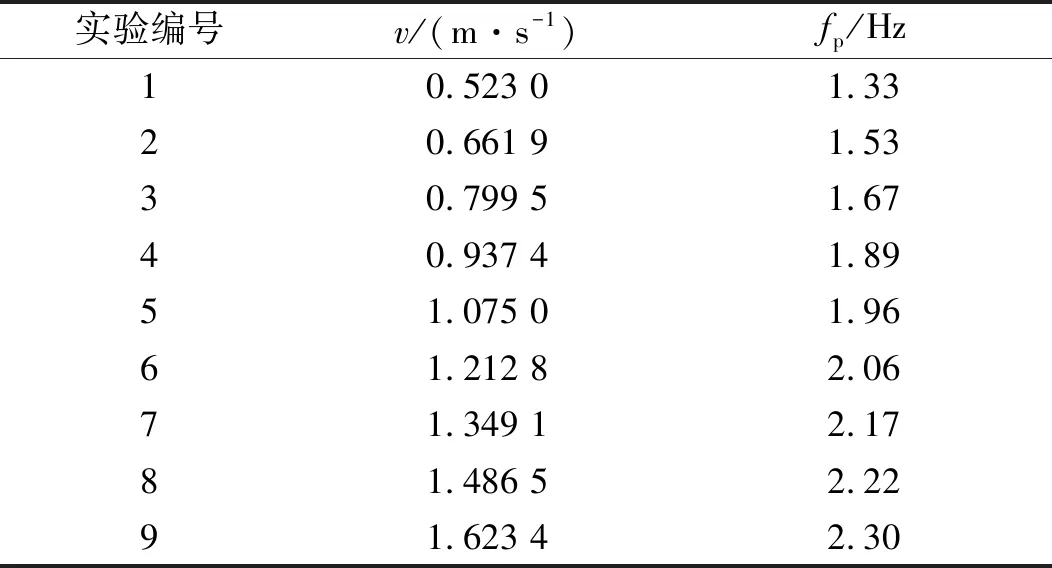
表7 实验数据基本信息

图5 滤波处理后的实测步行荷载时程曲线

实验方法、实测荷载参数的识别方法及识别过程与上节荷载模型相同，在这里就不再赘述。

3.2 识别结果

对9条步行荷载时程数据全部进行参数识别，其识别结果与测量曲线拟合结果对比如表8、表9和图6、图7所示。

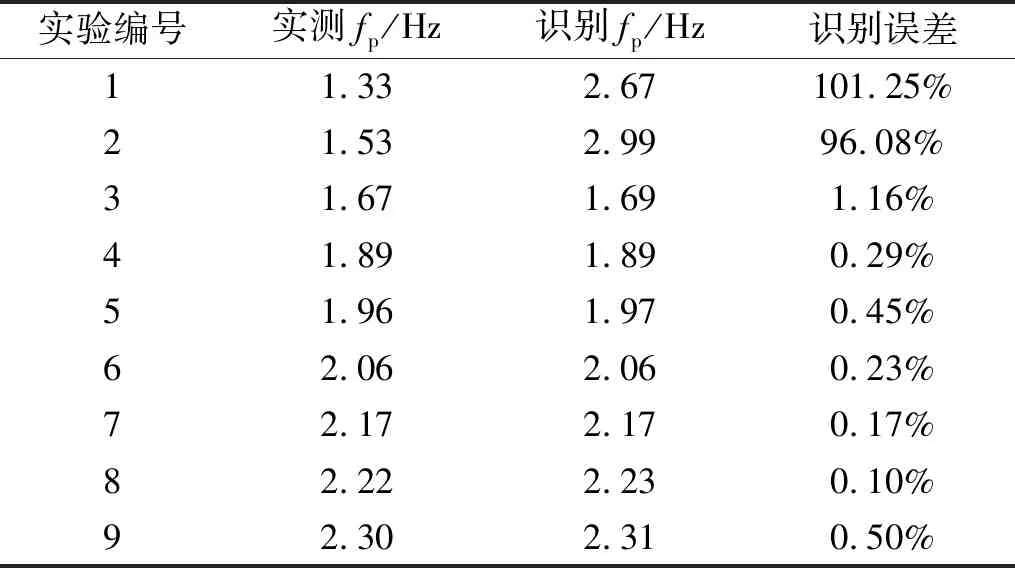
表8 步频对比

由以上结果可以得出，除实验编号1、2外，其他步行荷载的识别精度均在误差允许范围之内。考虑到人正常行走的频率范围是1.5～2.0 Hz，两阶段识别方法具有适用性。对于步频较低的情况，由于非正常步态造成荷载曲线较强的非周期性(图5曲线1、2)，导致算法的识别效果不理想。具体参数看，占步行荷载能量主导地位的前3阶的动载因子识别效果均较好。以上结果显示，两阶段识别方法可用于实际步行荷载的参数识别。

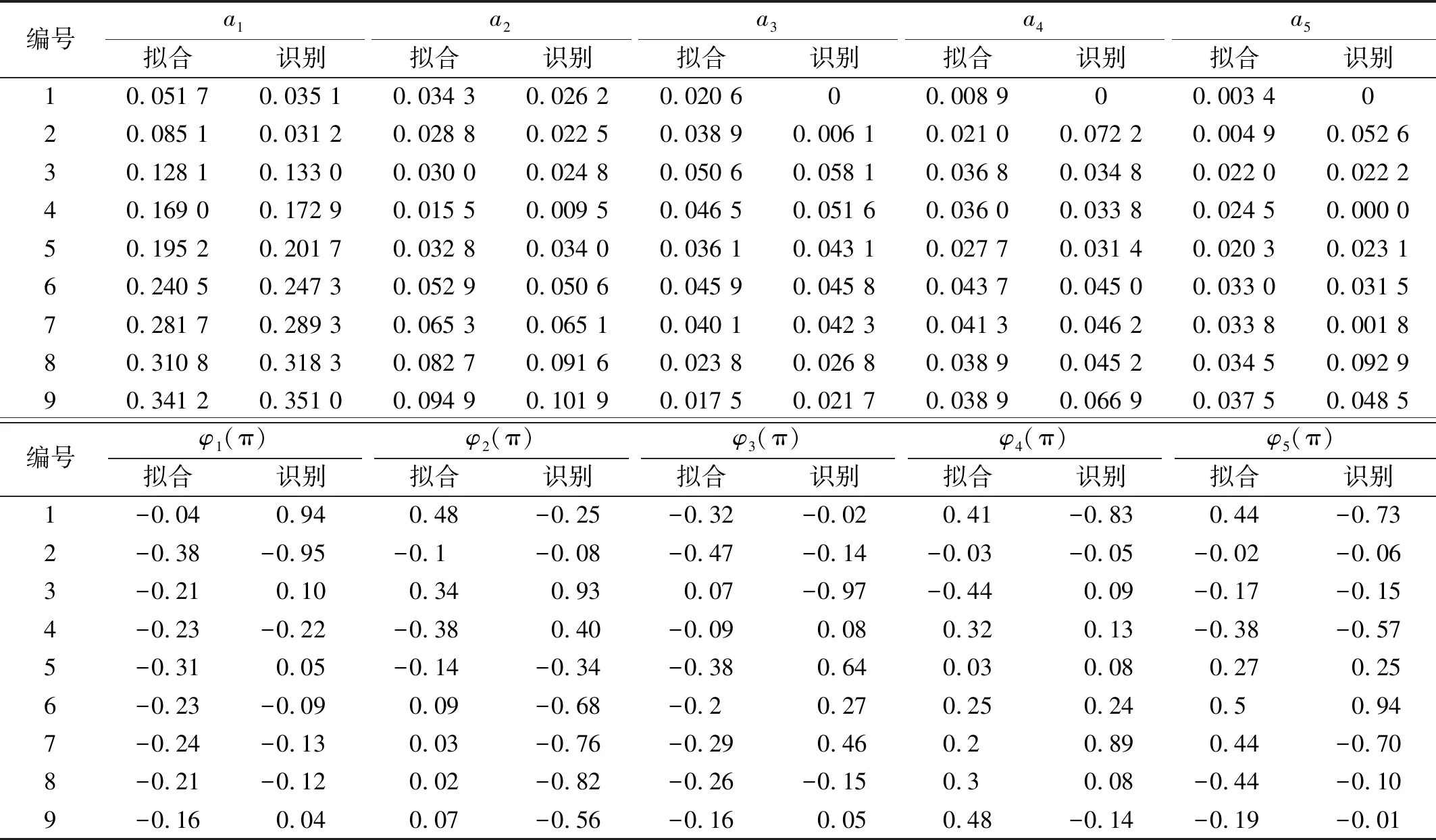
表9 动载因子和相位对比

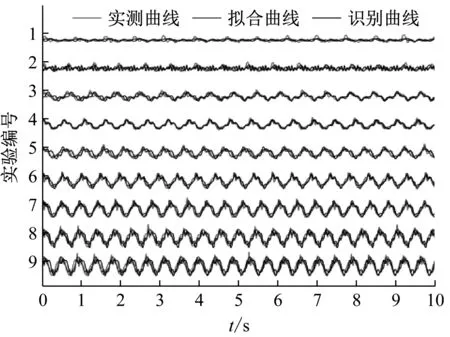
图6 模拟曲线与实测曲线荷载时程对比

Fig.6 Comparison of load time history between simulated curve and measured curve

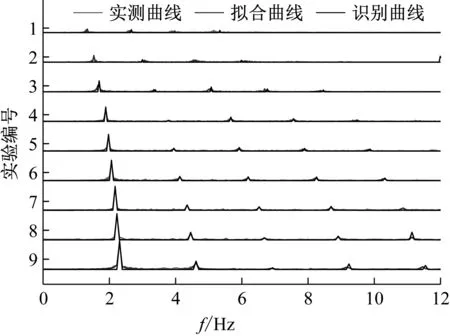
图7 模拟曲线与实测曲线傅立叶谱对比

4 结 论

从利用结构响应去研究步行荷载特性的角度出发，本文提出了采用两阶段遗传算法识别步行荷载模型参数的方法。第一阶段采用结构位移反应谱一致作为目标函数，识别动载因子、步行频率等荷载能量的总体要素；第二阶段采用结构位移时程一致作为目标函数，识别荷载相位角等局部要素。对步行荷载模型以及实测荷载的具体应用表明，两阶段识别方法可行，对初始参数不敏感，在正常步频范围内可以较为准确地获得荷载前5阶的相关参数。两阶段法相较一次识别方式，计算效率提升，并可有效避免局部收敛的问题。

本文将GA这一已经比较成熟的识别方法用于步行荷载的识别，验证了单人荷载建模的可行性。由于建立在给定荷载模型的基础上，方法没有直接考虑HSI。对于可能存在HSI效应的结构，本文方法可给出“响应等效”意义上的等效荷载，通过与刚性地面上荷载模型参数的比较，可进一步研究HSI的影响。此外，本文结果表明，可由结构响应获得人群荷载作用下的等效单人荷载，从而为研究人群荷载模型提供了反问题建模的新思路。