一种改进的迭代无迹卡尔曼滤波算法
2019-10-21陈波
陈 波
(新乡学院机电工程学院 河南 新乡 453003)
0 引 言
系统状态变量的精确估计对故障检测和控制应用有重要的作用。然而,非线性系统是不容易估计的,需要得到描述该运动的全概率密度函数。这种解决方案一般会受到多状态、不对称和不连续性等因素的影响。由于对全概率密度函数的形式没有限制,在一般情况下,它不能用有限的参数来表示。因此,任何实际的估计必须使用某些类型的近似值。目前许多不同类型的近似值已经得到应用,可是大多数的应用要么计算量难以处理,要么需要对难以实践的过程和观察模型做特殊的设想。主要由于这些原因,卡尔曼滤波(Kalman Filter,KF)一直是最广泛使用的估计算法。
张文等[1]分析了扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF),说明对于强非线性系统,UKF比EKF具有更强的优越性。张玉峰等[2]提出了一种基于平方根滤波的非线性卡尔曼滤波方法——自适应平方根无迹卡尔曼滤波方法,改进了传统的Sage-Husa自适应滤波算法,结合平方根无迹卡尔曼滤波算法进行非线性滤波。但其要确保系统状态和噪声方差阵的对称性和非负定性,增加了算法的计算量。李敏等[3]提出了一种改进的强跟踪平方根UKF算法,通过引入多重自适应衰减因子调节协方差矩阵,提高了滤波器的估计精度,但其估计精度的提高有限。张园等[4]提出s修正无迹卡尔曼滤波(SUKF)方法,虽然跟踪精度大幅提高了,但其增加了跟踪的计算量。黄平等[5]提出了一种基于量测一步预测信息的在线自调整的UKF算法,根据单步滤波的预测信息选取滤波时刻的最优滤波参数,进而实现算法的在线调整。基于该算法的UKF对于真实状态的跟踪效果优于固定参数的UKF。但其存在参数的取值范围增加有限,步长减小幅度有限等缺点,会导致计算量的急剧增加、算法的运行时间明显变长。Sarkka等[6]对非线性系统采用省略二阶以上高阶项得到线性化模型,只能在滤波误差及一步预测误差较小时才能适用,是一种次优滤波,跟踪精度的误差较大。文献[7]采用非线性函数传播估计系统状态的均值和协方差,但过程繁琐,需要频繁调节自由参数才能得到较好的跟踪效果。
KF在非线性系统中最常见的应用是扩展KF(Extended KF,EKF)的形式,EKF简单地使所有的非线性变换成线性化,并用雅可比矩阵代替KF方程中的线性变换。此外,如果测量和过程噪声协方差矩阵的先验信息是可用的,扩展卡尔曼滤波能进行非常方便快捷的实时处理,而且相当容易实现,通常由泰勒展开式进行线性化。由于忽略了高阶项,EKF的线性化会导致出现相应的状态估计错误,为了减少这种错误,通常采用二阶EKF。然而,这种方法在大测量数据问题的计算上有一定难度,减少这种误差的另一方法是线性化测量状态空间中的参考轨迹。这种方法被称为迭代扩展卡尔曼滤波(Iterated EKF,IEKF),该方法适合非线性仅存在于测量方程的情况[8]。虽然EKF保持了KF的优点和计算上效率递归更新的形式,但是它存在一些严重的局限性:(1) 如果误差可以用线性函数很好地近似模拟,线性变换就是唯一可靠的;否则该线性近似的效果会非常差。在最好的情况下,这破坏了滤波器的性能;在最坏的情况下,这会导致EKF的估计值全都偏离。然而,要确定这种假设的有效性是极其困难的,因为这取决于变换本身、当前状态的估计以及协方差的幅度。(2) EKF只有在各随机向量近似高斯分布的情况下才会有较好的近似,还不能满足复杂的密度、期望协方差表示。然而,这并非总是如此,一些系统包含不连续的其他的包含奇点,而在其他系统中,状态本身是固有离散的。(3) 在一些应用中,解析发现雅可比矩阵非常困难,需要使用雅可比矩阵的数值近似。但是,由于涉及到近似值而不是真实值,会导致出现其他类型的问题。初始状态估计的选择、滤波器参数的调整是标准EKF成功收敛的关键。(4) 在EKF中,卡尔曼增益矩阵取决于数据,滤波器的稳定性不再被假定。此外,滤波器特性的分析非常困难,扩展卡尔曼滤波不保证无偏估计。计算好的误差协方差矩阵,并不一定代表真实误差协方差,这些结果的分析也是很难处理的,采用无迹变换代替EKF从而得到无迹卡尔曼滤波(UKF)。
目前无迹变换已经在EKF框架中使用[9-10],与任意估计的非线性函数或变换相比,它使用直觉更容易估计的概率分布函数。状态分布是通过高斯密度估计的,它由一组确定性选择的采样点来表示。一些作者已经提出了通过一组确定性选择的采样点,使用后验密度的高斯分布来表示非线性滤波的思想[11-12]。非线性滤波器的整个等级(包括UKF)被称为线性回归卡尔曼滤波器,因为它们都是基于统计的线性化,而不是分析线性化(如EKF)。统计线性化是通过回归点的线性回归进行的,这些样本点完全地记录了真实的均值和高斯密度的协方差。当非线性系统使用时,它们准确记录了任何非线性的二阶(泰勒级数展开)的真正均值和协方差[13]。
UKF产生的性能在线性系统上等同于卡尔曼滤波器,而且不用EKF所需的线性化步骤就成功推广到非线性系统。在严格非线性系统下,该UKF持续达到的精度水平比EKF更高。而且UKF和EKF的计算复杂性是在相同的指令下完成的。
本文提出了一种改进的迭代无迹卡尔曼滤波(Improved Iterated Uncented Kalman Filter,IUKF)算法。在系统方程严重非线性的时候,它比UKF和IEKF算法具有更好的性能。该方法使用了一步预测步骤和过滤的更新步骤的线性统计分析。
1 卡尔曼滤波算法
UKF是无偏转换到递归状态估计的简单扩展。无偏转换是用于计算对经历了非线性变换的随机变量进行统计的方法,UKF使用直觉来简化概率分布函数,而不是近似任意的非线性函数或变换。按照这种直觉,产生一组点,称为σ点,其样本均值和样本协方差为x(k|k),第k次迭代的状态估计和P(k|k)状态协方差矩阵。依次对这些点中的每一个应用非线性函数以产生变换的样本,并且从转化的样本计算预测的平均值和协方差。
这在表面上类似于蒙特卡罗方法,但是样本没有随机生成。相反,样本被确定性地选择,使得它们捕获关于分布的特定信息。一般来说,这种直觉可以应用于捕获关于多类型多种类的分布信息。在这里,我们考虑捕获假设高斯分布的均值和协方差的特殊情况。
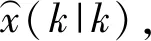
(1)
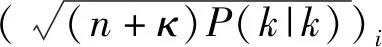
2 迭代无损卡尔曼滤波
由式(1)选择的样本集与x(k)的分布具有相同的样本均值、协方差和更高的奇数中心矩。矩阵平方根和k影响σ点的第四和更高阶样本矩。
考虑以下非线性滤波问题:
x(k+1)=fk(x(k),w(k))
z(k)=hk+1(x(k))+v(k)
(2)
式中:x(k)是系统在时间步长k的向量状态,w(k)是由干扰和建模误差引起的向量噪声过程,z(k) 是观测向量,v(k) 是加法测量噪音,假设噪声向量w(k)和v(k)为零均值:
E[w(i)wT(j)]=δijCv(i)
E[v(i)vT(j)]=δijCv(i)
E[v(i)wT(j)]=0∀i,j

(3)
然后执行如下的预测步骤:
(4)
预测协方差矩阵为:
(5)
使用标准向量和矩阵运算计算平均向量和协方差矩阵,这意味着算法适用于任何选择的过程模型。该算法实现方便,不需要评估EKF中需要的雅可比矩阵,比通过分析线性化确定的预测更准确。
更新步骤:通过观察测量z(k)获得的知识细化密度函数。使用贝叶斯定理对无记忆感觉系统的条件密度产生:
p(x(k)|Z(k))=p(x(k)|Z(k-1),Z(k))=
(6)
式中:Z(k)是收到的从Z(1)到Z(k)的一组观察值,c是归一化常数:
c=∮x(k)∈Xp(Z(k)|x(k),p(x(k)|Z(k-1)))dx(k)
近似的前提是认为预测状态和测量噪声都是正态分布的。这样,后验概率密度p(x(k)|Z(k))是两个高斯分布的结果,也是一个高斯分布,因此,MMSE估计符合MAP估计。目前的任务是找到最大的后验概率密度,通过排除不相关的常量和因子并最大化其对数后,可以归结为最小化以下函数:
(7)
(8)
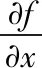
(9)
可以从式(7)中得到F(x)的清晰的雅可比矩阵和Hessian矩阵:
(10)

式(10)和式(9)的差产生如下迭代形式:
(11)
(12)
3 仿真结果与分析
下面将提出的新算法应用于通过线性动态系统方程跟踪假定目标的状态估计问题,其测量方程中存在一些非线性,并和UKF、IEKF两种算法的性能进行对比。主要比较新提出的滤波器和UKF、IEKF两种算法在处理状态动态方程和测量方程存在非线性时的性能。考虑以下状态估计问题:
x1(k+1)=-kx2(k)+w1(k)
x2(k+1)=-exp[10-2x2(k)]+w2(k)
z(k)=x1(k)x2(k)+v(k)
(13)
设置采样时间T=0.03 s,其中z(k)是接收到的k时刻的观测数据,w1(k)、w2(k)、v(k)是独立的零均值加性高斯噪声过程,v(k)的方差为100,且具有:
假设噪声向量w(k)和v(k)为零均值独立噪声。从线性状态方程中可以得出x1和x2可以分别解释为目标的位置和目标的速度。用均方根误差(Root Mean Square Error,RMSE)表示平均值,作为衡量跟踪性能的标准,并进行80次蒙特卡罗试验。RMSE能较好地表示系统的估计精度,其表达式为:

新的改进的迭代无迹卡尔曼滤波的优越性如图1和图2所示。与改进的迭代无迹卡尔曼滤波算法相比,IEKF与UKF的性能表现很差,结果的差异非常显著。
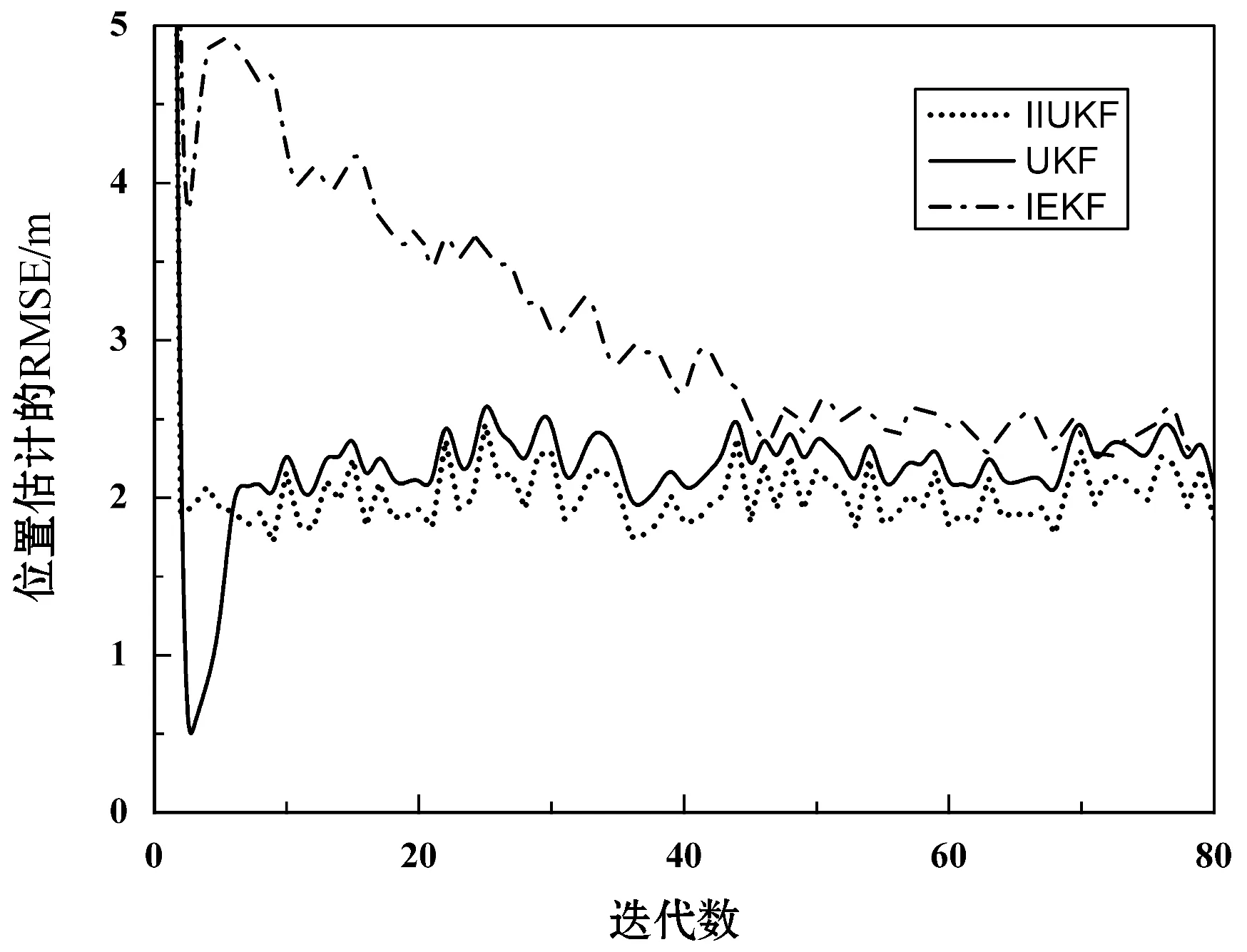
图1 位置估计的RMSE比较
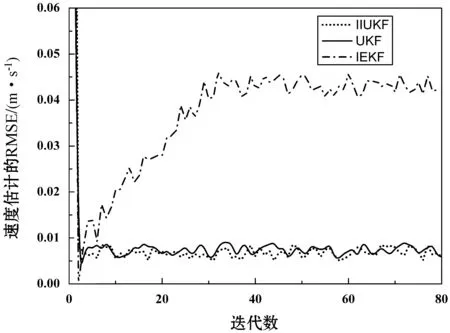
图2 速度估计的RSME比较
由图1、图2可以得出,运动状态的非线性越严重,通过IEKF和UKF得到的状态估计的错误越大。而IIUKF算法在状态方程中存在严重非线性时能表现出更好的性能,而且它还具有较好的稳态误差的能力。
4 结 语
本文引入了一种改进的无迹卡尔曼滤波算法,在运动状态方程合测量方程出现较严重的非线性时,由该算法生成的滤波器比无迹卡尔曼滤波算法(UKF)、迭代扩展卡尔曼滤波(IEKF)有更高的准确率,并通过实验证明了它的有效性。新滤波器比较容易实现且具有较高的准确估计性,比另外两种算法在非线性方面得到更多的应用。
