混沌自适应水波算法在包装配送问题中的应用

彭 维

(重庆城市管理职业学院工商管理学院 重庆 401331)

0 引 言

包装配送问题是典型的组合优化问题[1]，通常可以描述为：从一个配送中心出发，安排若干车辆为客户配送包装，要求在满足交货时间、车辆载重、客户需求量等条件下，合理安排配送线路，使配送的路程、时间或者费用达到最优。近年来，随着电子商务深入发展，包装需求量和配送量井喷式增长，包装配送问题愈发受到重视，其求解算法也逐渐成为了学者们的研究热点。

分析大量文献可知，包装配送问题的求解算法可以分为精确算法和启发式算法，其中启发式算法占比高达85%左右。这主要是由于包装配送问题属于NP-hard难题，可行解数量会随着问题规模的增大而发生“组合爆炸”，计算开销也随之呈指数式增长[2-3]。精确算法在求解该类问题时，求解效率低、运行速度慢，往往无法取得令人满意的结果。相比之下，启发式算法具有快速寻优能力，可以在较短时间内求得大规模问题的较好解，因此成为了包装配送问题的主要求解算法。目前，应用于包装配送问题的主要启发式算法包括：遗传算法[4]、萤火虫算法[5]、禁忌搜索算法和其他算法[6]。

虽然已有大量优秀算法，但追求更高效的算法一直都是包装配送及其他组合优化问题的重要研究方向[7]。对此，本文引入一种新型启发式算法—水波算法(WWA)，并将其应用于包装配送问题中。WWA算法由郑宇军教授于2014年首次提出，具有参数较少、实现简单、计算开销小等优势[8]。在标准WWA算法基础上，本文对算法个体编码方式进行重新设计，并引入混沌机制和碎波系数自适应调整机制，提出了基于包装配送问题的CAWWA算法。实验表明，CAWWA算法能够很好地适用于包装配送问题的求解。

1 包装配送问题的数学模型

假设配送中心安排K辆车为L个客户配送包装，车辆最大载重量为Q，客户需求量为qi(i=1,2,…,L)，用i=0表示配送中心，cij表示客户i到j的配送成本(如距离、费用等)，定义决策变量为：

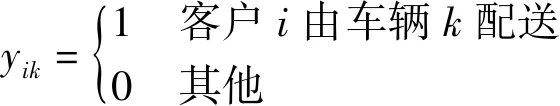
则包装配送问题的数学模型可表示为[9]：

(1)

(2)

(3)

(4)

(5)

(6)

xijk=0或1 ∀i,j,k

(7)

yik=0或1 ∀i,k

(8)

其中:式(2)表示车辆最大载重约束；式(3)-式(5)表示每个客户都有且仅有一辆车配送；式(6)表示消除子回路；式(7)-式(8)表示变量取值范围。

2 标准水波算法

2.1 基本原理

WWA算法是模拟浅水波运动模型求解问题的过程而设计的一种新型启发式算法[10]。算法将问题求解空间看作为海床，每个可能解看作一个波高为h和波长为λ的水波。水波的适应度值与水波到海床的垂直距离成反比，即水波距海床越远，适应度值越小，内含能量也越小，且波长λ越长，波高h越低，这使得优质水波可以在最优解附近进行局部搜索，而劣质水波则能够跳出局部最优进行大范围搜索，进而求得问题最优解。WWA算法包括传播、折射和碎波3个算子。不同深度水域的波形如图1所示。

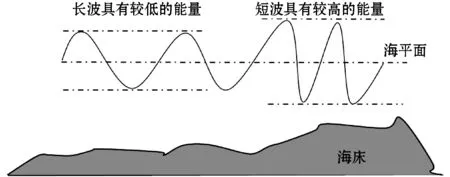
图1 不同深度水域的波形

2.2 传播算子

假设问题维度为D，水波每一维位置为x(d)(1≤d≤D)，每次迭代中水波通过传播公式对自身位置进行更新。

x′(d)=x(d)+rand(-1,1)·λ·L(d)

(9)

式中:rand(-1,1)表示[-1,1]之间的均匀随机数；L(d)表示第d维搜索空间的长度。位置更新后，如果适应度函数值f(x′)>f(x)，则用x′代替x，水波波高h重置为最大值hmax；反之，保留x，水波波高h伴随能量的损耗而衰减。水波位置更新后，水波波长也发生改变，公式如下：

λ=λ·α-(f(x)-fmin+ε)/(fmax-fmin+ε)

(10)

式中：α表示最大波长减少率；ε表示为保证分母不为0而设置的极小正数；fmax、fmin分别表示本次迭代中最优水波和最差水波对应的适应度值。分析式(10)可知，波长与适应度值成反比。适应度值越大，水波波长越短，传播范围越窄；反之，水波波长越长，传播范围越大。

2.3 折射算子

水波传播过程中，有的水波会在浅水域聚集，最终在深水域发散反射。具体来说，当水波波高h变为0时，水波将进行反射，对应位置根据下式进行更新：

(11)

式中：x*(d)表示当前种群的最优水波，N(μ,δ2)表示均值为μ、标准差为δ的高斯随机数。折射后的波长为：

(12)

2.4 碎波算子

随着能量的不断增加，水波波峰变得越来越陡峭，最终破碎成大量独立的小波浪。WWA算法只对最优水波进行碎波操作，公式如下：

x′(d)=x*(d)+N(0,1)·β·L(d)

(13)

式中:β为碎波系数。碎波操作后，如果f(x′)>f(x*)，则用x′代替x*；否则，不更新。

3 混沌自适应水波算法

3.1 个体表达式构造

步骤1：生成随机矩阵。随机生成一个L×L(L表示客户数量)的客户矩阵M，每个元素mij(i、j为横坐标和纵坐标)的值介于0～1之间。

步骤2：生成概率矩阵。对矩阵M每一行进行归一化处理，得到概率矩阵M1。比如，假设M第一行为[0.20.30.80.9]，对应四个元素相加之和为0.2+0.3+0.8+0.9=2.2，各元素分别除以2.2，可得归一化处理结果为[0.090.140.360.41]，将其作为M1的第一行。同理，可生成M1其他数据。可知，M1中每一行元素之和均为1，且每个元素表示该客户在客户序列中某个位置的概率。比如，假设M1的第一行为[0.090.140.360.41]，则表示第一个客户排在第一位的概率为0.09，排在第二位的概率为0.14，排在第三位的概率为0.36，排在第四位的概率为0.41。

3.2 个体表达式解析

步骤1生成0-1矩阵。将概率矩阵M1元素与波长λ进行比较，若小于λ，则相应位置为1，反之为0，得到0-1矩阵M2，如图2所示(假设λ=0.2)。进行矩阵调整，确保M2每行每列都只有一个1。调整原则为：如果第i列只有一个1，则保留该1，如图2的第2列；如果第i列不止一个1，假设所有1后面的列都还有1出现，则优先保留第一个1，假设有的1后面的列全是0，则优先保留该1，其他1变为0，如图2中的第1列和第3列。

步骤2生成配送路径。根据M2生成客户序列，并按照车辆载重约束生成配送路径。图2中客户序列为x=3-1-4-2。假设客户1到客户4的包装需求量分别为50、20、40和20，车辆最大载重量为70。则可得两条配送子路径，分别为x1=0-3-1-0(0表示配送中心)，x2=0-4-2-0。每条子路径的配送成本(距离、费用等)之和即为该方案的配送成本。

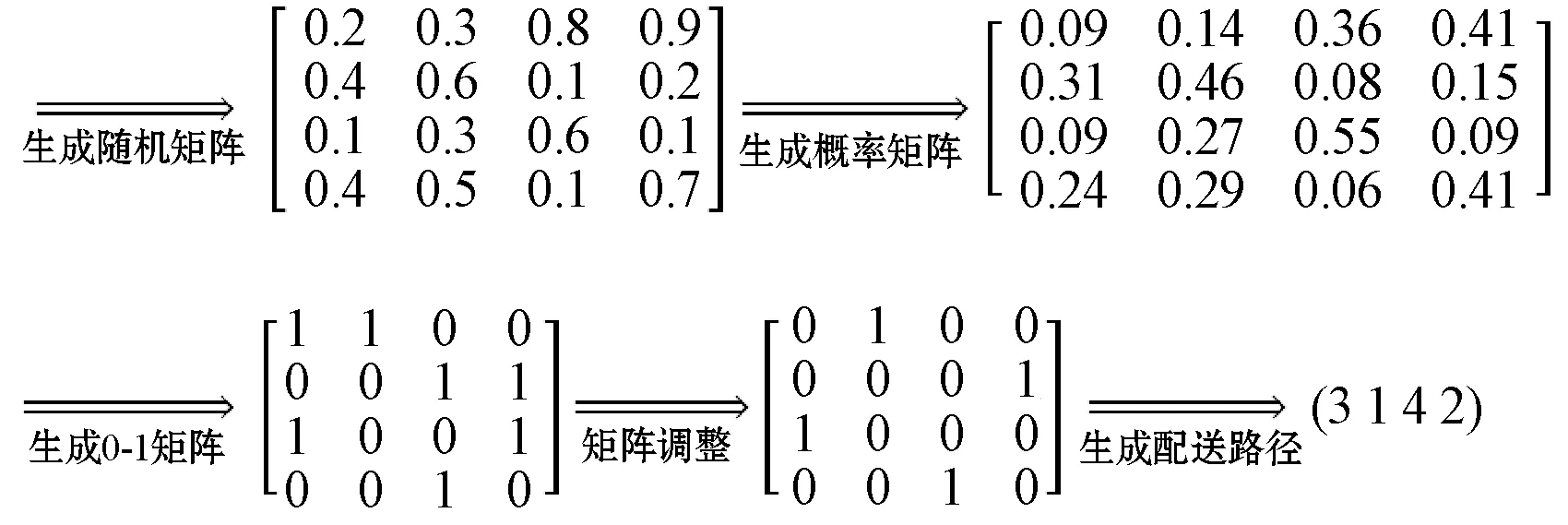
图2 个体表达式构成及解析

3.3 混沌初始化

启发式算法对初始种群具有严重依赖性，如果初始种群个体在最优解邻域内，那么算法能够快速收敛到较好解甚至最优解。如果初始种群个体离最优解较远，则算法收敛速度较慢，且求解精度会大幅降低。混沌是一种广泛存在于社会和自然界中的非周期性运动，具有随机性、遍历性和规律性等特征，能够在一定范围内不重复地遍历所有状态[11-12]。对此，本文采用混沌机制来克服启发式算法初始种群分布不理想的缺点，以提高初始种群质量。本文采用混沌Logistic映射生成初始随机矩阵，公式如下：

Mn+1=μMn(1-Mn)

(14)

n=0,1,2,… 0≤μ≤4

(15)

3.4 碎波系数自适应调整

在WWA算法中，碎波算子主要用于对最优水波附近的空间进行搜索，而碎波系数β是控制搜索范围的一个重要参数。β越大，搜索范围越广，反之则搜索范围越小。传统WWA算法采用固定的碎波系数，明显无法满足算法前期和后期的不同搜索需求，无法达到全局搜索和局部搜索的平衡，不利于算法求解质量的提高。对此，本文提出了基于对数递减的碎波系数自适应调整机制。在算法前期，碎波系数较大，算法可以大范围地进行全局搜索，从而得到更优的水波。而在算法后期，碎波系数较小，算法能够更加精准地进行局部搜索，进而提高算法求解精度。公式如下：

β=βmax-γ(βmax-βmin)×logiterMaxiter

(16)

式中:βmax、βmin分别表示最大最小碎波系数；γ表示对数调整因子；iter表示算法当前迭代次数，iterMax表示最大迭代次数。

3.5 CAWWA算法求解包装配送问题

步骤1设置算法参数，包括初始种群规模Num、初始水波波高hmax、波长λ、波长减少率α、最大碎波系数βmax、最小碎波系数βmin、对数调整因子γ和算法最大迭代次数iterMax，令当前迭代次数iter=0。

步骤2根据第3.3节生成Num个初始随机矩阵。

步骤3判断iter是否大于或等于iterMax。若是，算法停止，输出最优水波x*及f(x*)；反之，算法进入步骤5。

步骤4按照第3.1节对个体矩阵进行归一化处理，并根据第3.2节解析个体并计算适应度值，记录最优水波x*及适应度值f(x*)。

步骤5利用式(9)对每个水波x进行传播，得到新的水波x′，利用式(10)更新波长λ。如果f(x′)>f(x)，则用x′代替x，重置波高为hmax；反之，保留x，令波高h=h-1。

步骤6判断水波波高h是否等于0。若是，则利用式(11)-式(12)进行折射操作。

步骤7利用式(13)对最优水波x*进行碎波操作，得到新的水波。如果f(x′)>f(x*)，则用x′代替x*；反之，保留x*。

步骤8令iter=iter+1，返回步骤3。

4 仿真实验

为验证算法有效性，本文在8×quad core 2.3 MHz CPU、64 GB内存、Window10系统环境下，利用CAWWA算法对包装配送实例进行仿真测试。其中，配送中心位置为(30 km,30 km)，30个客户需求量及位置信息如表1所示，车辆最大载重为8 t。

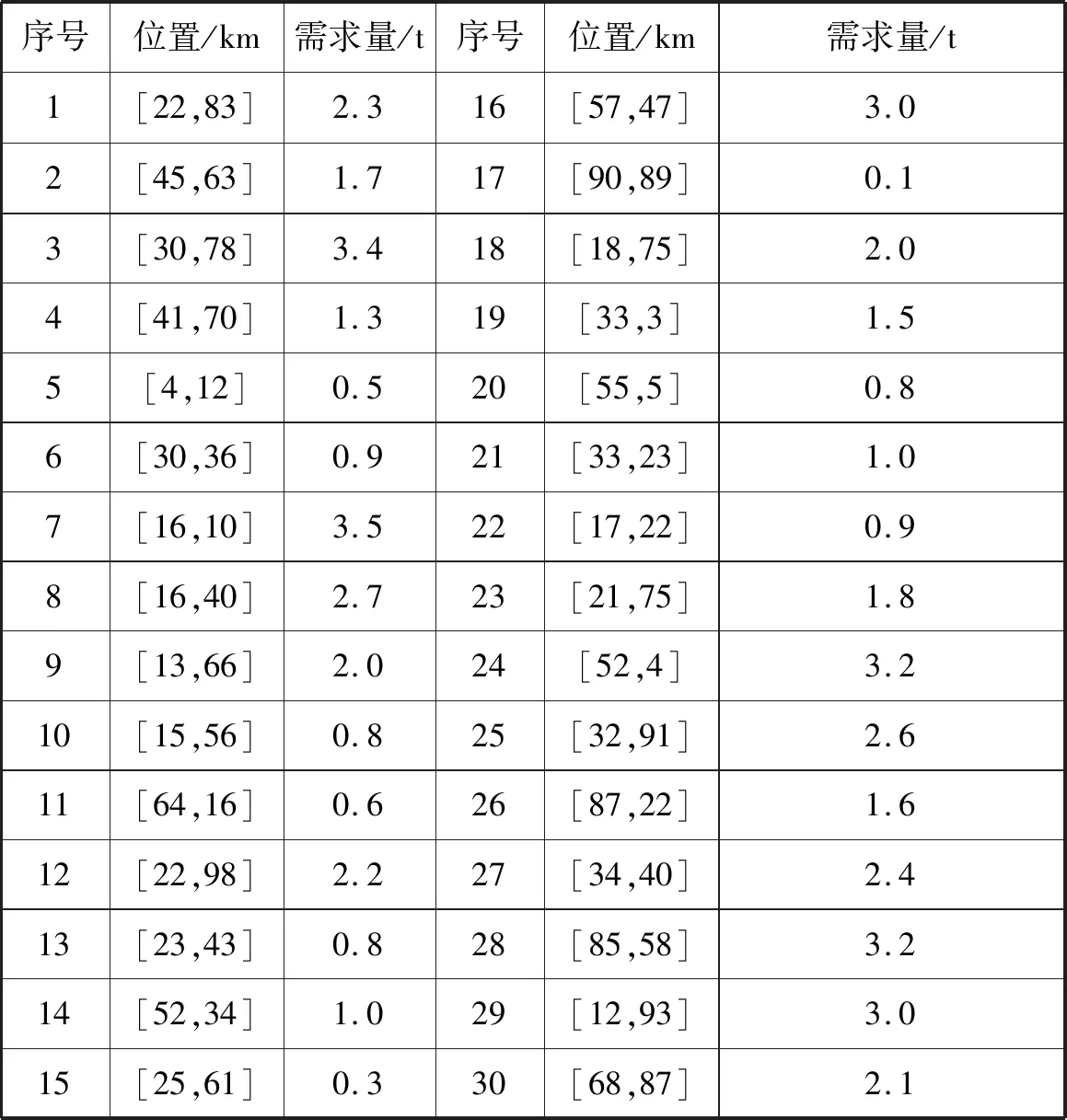
表1 客户信息

如表2所示，完成此次配送任务所需车辆数为8，最优配送距离为809.59 km。由此可知，CAWWA算法能够有效应用于包装配送问题的求解。为进一步验证算法的求解性能，分别利用CAWWA算法、GA算法[13]、ACO算法[14]和TS算法[15]对配送问题的国际通用算例进行50次求解，统计求得最好解(BS)、平均运行时间(AT)等指标如表3所示。各算例最优配送路径如表4所示。

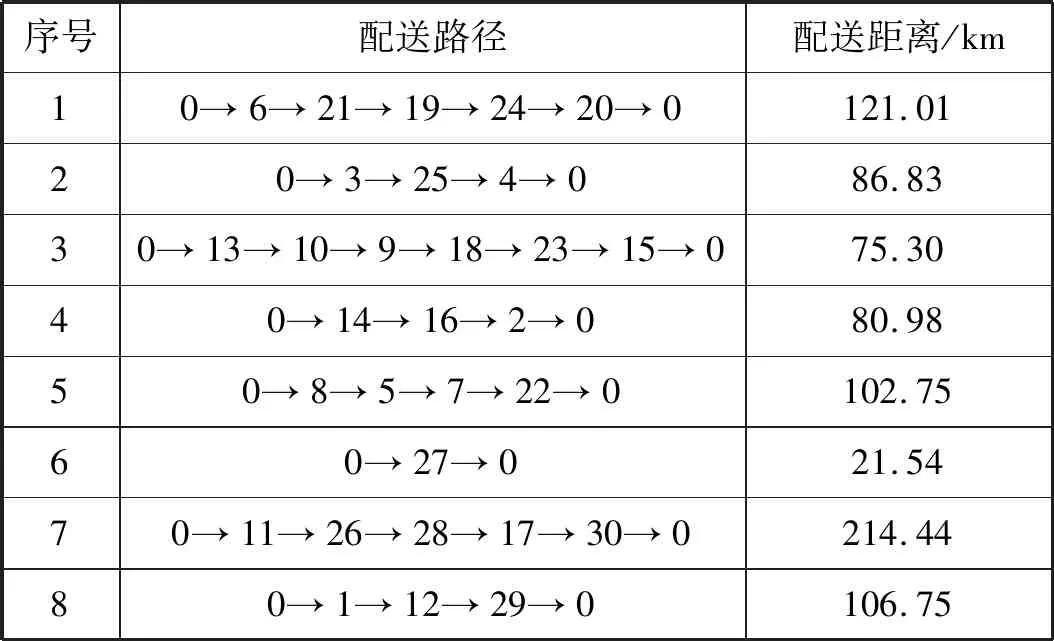
表2 最优配送方案

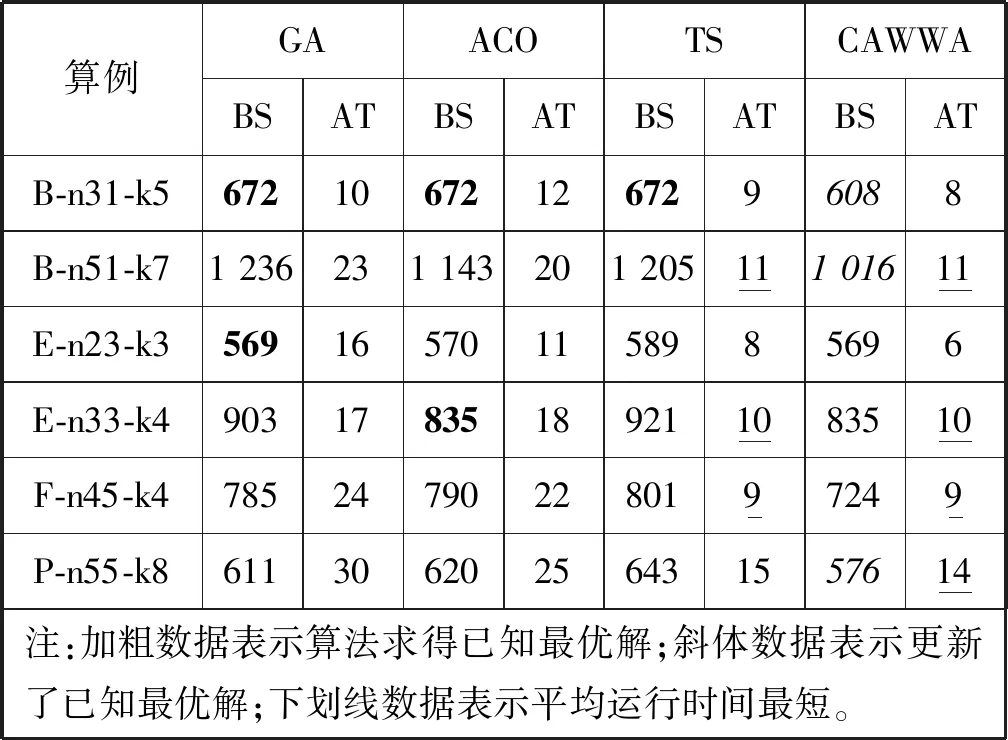
表3 GA算法、ACO算法、TS算法和CAWWA算法仿真结果对比

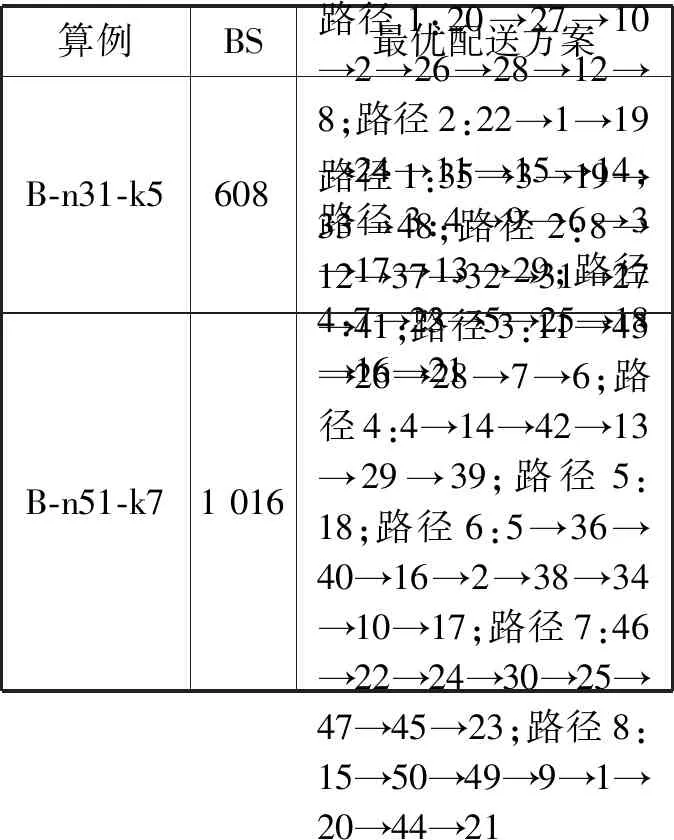
表4 最优配送方案

续表4

由表3可知， TS算法只能求得B-n31-k5算例的已知最优解，GA算法和ACO算法分别还能求得E-n23-k3、E-n33-k4算例的已知最优解，CAWWA算法不但能求得所有算例已知最优解，还更新了B-n31-k5、B-n51-k7和P-n55-k8的已知最优解。由此可见，CAWWA算法全局寻优能力最强，GA算法和ACO算法次之，而TS算法最弱。同时，CAWWA算法求解各算例的平均运行时间最短，说明该算法运行速度最快、搜索效率最高。这主要得益于混沌机制提高了算法初始种群质量，自适应碎波系数增强了算法前期全局搜索能力，并提高了算法后期的搜索精度，进而优化了算法综合求解性能。

综上分析，CAWWA算法能够很好地适应包装配送问题的求解，且求解性能优于GA算法、ACO算法和TS算法。

5 结 语

本文主要对求解包装配送问题的CAWWA算法进行了研究。首先，设计了基于包装配送问题的个体编码方式；然后，引入混沌机制生成初始种群，并提出了自适应调整的碎波系数，扩大算法前期搜索范围，提高后期搜索精度。仿真结果表明，CAWWA算法求解性能优于GA算法、TS算法和ACO算法，能够适应于包装配送问题的求解。