基于EKF+EKS的BCG动态高斯模型滤波研究

王子民 甘智宇 刘振丙

1(桂林电子科技大学计算机与信息安全学院 广西 桂林 541000)2(桂林电子科技大学电子工程与自动化学院 广西 桂林 541000)3(广西自动检测技术与仪器重点实验室 广西 桂林 541000)4(广西信息科学实验中心 广西 桂林 541004)

0 引 言

BCG信号是心脏在周期性地泵血过程中产生的微弱且复杂的作用力[1]。基于牛顿第三定律，在心脏规律的收缩和舒张过程中，血液流经动静脉又回到心脏的过程会对人体产生反作用力。当血液因心房和心室的收缩流出时对人体产生作用力;当经过血管不同位置，尤其是流经大血管的弯曲处时由于冲击力作用对身体产生反作用力；血液流动时血管的弹性运动产生的作用力。以上三种作用力的合力引起了心冲击运动[1-2]，心冲击图信号源于心脏机械收缩以及大血管中的血液被突然加速而对身体产生的反作用力，因此BCG信号可以反映心脏的机械活动[3-4]，图1所示为BCG信号波形。

心脏病已经成为了国民健康的最大威胁，BCG信号可为心脏疾病提供有效的检测、诊断和治疗信息[5]。BCG信号单周期内有相同的6个特征点，但每个周期形态有差异，同一人在不同健康状态或者不同环境条件采集的BCG信号有差异。随着研究的深入，科研和医务人员均需要克服采集环境和个体差异影响的正常健康个体BCG信号，McSharry[6]提出的心电图(Electrocardiogram，ECG)信号动态高斯模型和Almasi[7]提出的心音(Phonocardiogram，PCG)信号的动态高斯模型，由于BCG信号、ECG信号和PCG信号均属于生物医学的微弱信号，因此可以设计一个合成BCG信号的动态高斯模型。

基于微弱信号的动态模型必然关注两个方面：滤波算法和系统的动态模型。BCG的动态高斯模型合成的信号属于非线性周期信号，因此必须采用自适应的非线性的滤波方法。通过比较经典滤波方法、小波去噪和扩展卡尔曼滤波(Extended Kalman filter，EKF)对BCG信号进行滤波，因为BCG信号太微弱，单一的滤波方法不能满足滤波要求。由于Reza Sameni[8]已将扩展卡尔曼滤波和扩展卡尔曼平滑运用至ECG信号的降噪，基于EKF和扩展卡尔曼平滑(Extended Kalman smoother，EKS)的特性。本文提出一种联合扩展卡尔曼滤波和扩展卡尔曼平滑滤波方法对BCG信号进行复合滤波。由于EKF滤波是需要微弱信号真实值的，但信号的真实值通常不能确定，需要动态模型的值来作为BCG信号真实值的估计值，因此可将动态高斯模型模合成信号的数值作为滤波过程中真实值的估计值。

1 相关工作

1.1 ECG信号动态高斯模型

2003年McSharry提出一种基于高斯函数的ECG信号动态高斯模型[6]，该模型可以合成健康个体的ECG信号，ECG信号的任何一点都可以用笛卡尔坐标(x,y,z)表示，函数方程组如下所示：

(1)

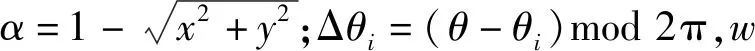
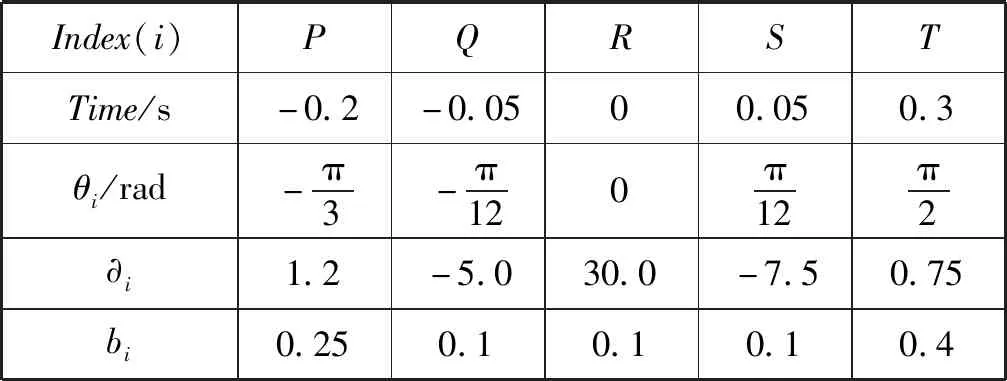
表1 ECG模型参数

1.2 PCG信号动态高斯模型

2011年Almasi提出一种PCG信号的动态模型[7]，能合成正常健康个体的PCG信号。PCG信号的动态模型是基于高斯核函数的动态模型，与ECG信号不同的是，PCG信号模型的高斯核函数表现形式采用极坐标的形式。心动周期包括心脏收缩期和舒张期，心音信号可以分为4个阶段，S1、S2、S3和S4。S3和S4必须通过特殊手段才能测听到，相对而言S1和S2比较容易测听到，因此PCG信号的动态模型，通常只研究心音信号的前两个阶段S1和S2。PCG信号的高斯函数动态模型极坐标形式方程组如下：

(2)

式中：θ=atan2(y,x)代表信号的相位值，取值范围-π≤θ≤π，w代表角加速度，αi、μi和σi对应于方程组高斯核函数的幅度、宽度和相位等参数，fi代表频率，φi代表相位的迁移。与ECG信号动态高斯模型相同，只要模型参数确定后，PCG信号的动态高斯模型合成的PCG信号的波形和周期也就确定。PCG信号模型参数如表2所示。

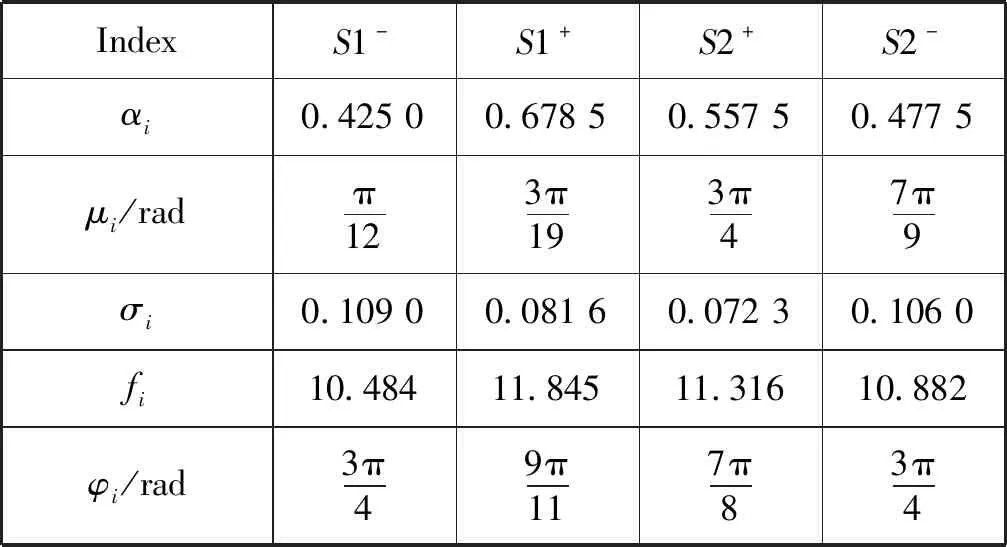
表2 PCG模型的参数

通过选择不同的模型参数来合成不同形态和不同周期的PCG波形，为评估处理医学信号PCG的方法提供基准。本文关于BCG信号动态高斯模型的灵感来源于ECG信号和PCG信号的动态高斯模型，由于BCG信号、ECG信号和PCG信号有许多相似的地方，都属于生物医学微弱信号，具有信号频率低、幅值低和噪声强等特点。因此可将ECG信号和PCG信号动态高斯模型的思想运用到BCG信号。

1.3 扩展卡尔曼滤波和扩展卡尔曼平滑

卡尔曼滤波不能直接用于非线性滤波，本小节主要阐述EKF的滤波框架[9]。EKF通常适用于离散的非线性系统，一个离散的系统可以表述如下:

(3)

(4)

其中:Ak、Fk、Ck、Gk定义如下：

(5)

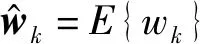
扩展卡尔曼滤波包括两个阶段，预测和更新。预测是根据过去的状态判断当前状态的值，更新阶段指的是当前状态的测试信息，用于重新精确修改之前的状态值，之前的状态值结果会反馈当前状态的值。

预测方程为：

(6)

创新方程为：

(7)

更新方程为：

(8)

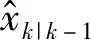
扩展卡尔曼平滑起源于卡尔曼平滑，EKS也是卡尔曼平滑通过泰勒级数一阶展开忽略高次项的扩展方法，EKS相对扩展卡尔曼滤波前向滤波是反向平滑滤波，因篇幅有限，此处不再叙述，有兴趣的读者可以阅读文献[10-12]。

2 方 法

2.1 BCG信号的采集

BCG信号的采集使用压电薄膜(PVDF)传感器[9]，安装在凳子上，属于无创伤测试方案，对用户测试造成的心理压力比较小。PVDF属于模拟电压传感器，属于线性传感器，压电薄膜所受到的压力与输出电压呈正相关[14-15]。电荷放大电路主要是将电压信号放大，通过低通滤波后放大信号。电压跟随器的主要作用是隔离前后一级的低通滤波放大电路[13-15]。BCG信号的前端模拟处理电路的硬件框图如图2所示。

图2 BCG信号采集和模拟电路处理

2.2 BCG信号动态高斯模型

BCG波形包含F波、G波、H波、I波、J波、K波、L波和M波，每一个波代表相邻区域的一个极大值或者极小值。F波和G波在IJK波群之前，G波位置紧随F波之后，均属于不明显的波形，F波和G波反映了心脏收缩早期活动。心脏收缩开始期是H波，I波和J波属于心脏收缩期的主要特征，J波位于I波之后，且J波具有BCG波形的最大幅值，K波是心脏收缩期结束的标志。L波位置在K波之后，M波位置在L波之后，N波属于BCG波形的最后阶段。L波和M波属于心脏舒张早期，N波属于心脏舒张中期和末期。由于N波波形特征不明显，F波和G波也如此，通常忽视掉这三个波形。BCG波形特征也就主要体现在H波、I波、J波、k波、L波和M波[4]。基于上述原理，本文的BCG信号动态高斯模型主要包含上述6个波的完整特征。ECG信号与BCG信号的波形相似度比较高[16]，BCG波形和ECG波形均是频率低、幅值低和噪声强等特点，且都是通过信号的波峰和波谷表示信号特征，因此可用下式表示[6-7]：

式中：θ表示信号的相位，b表示信号的宽度，α表示信号的幅值，高斯核函数的就是将BCG信号的特征点H波、I波、J波、K波、L波、M波的每一个特征点用幅值、宽度和相位来表示。z0表示为呼吸作用，z0(t)=Asin(2πf2t)表示随着呼吸频率而产生的BCG信号的基线A=0.15 mV[6]。

2.3 联合扩展卡尔曼滤波与扩展卡尔曼平滑的复合滤波

本论文对BCG信号采用的降噪滤波方法有4种，经典滤波方法指传统的数字滤波高通、低通和带通滤波器有较好的滤波效果[8,17-18]。经典的BCG信号数字滤波方式是采用高通滤波滤除呼吸信号，低通滤波滤掉因为环境因素、肢体活动带来的干扰，最后是工频滤波去除50 Hz的工频干扰信号[20]。小波滤波采用的是DB5小波进行6尺度对BCG信号进行分解。卡尔曼滤波通常只适用于线性系统[17-18]，用于非线性的信号滤波表现不佳。

由于BCG信号属于非线性的准周期信号。若想将卡尔曼滤波用于BCG信号处理，则必须将卡尔曼滤波的线性关系转化为非线性的关系，因此可采用扩展卡尔曼滤波方法。最常用的方法是卡尔曼滤波通过泰勒级数一阶展开忽略高次项的扩展方法。在此基础上形成扩展卡尔曼滤波[16-17]。卡尔曼平滑滤波也通常适用于线性系统的滤波。EKS也是卡尔曼平滑通过泰勒级数一阶展开忽略高次项的扩展方法。EKF主要有两大缺陷，其一是未考虑信号的分布误差，其二是认为独立的线性系统产生状态误差[21]。当微弱信号经过EKF滤波后，可再经过EKS滤波，而EKS反向平滑滤波可缩小信号的分布误差和非线性系统产生的状态误差。

本文采用一种基于联合扩展卡尔曼滤波与扩展卡尔曼平滑的方法对BCG信号进行复合滤波。扩展卡尔曼滤波是正向迭代滤波，扩展卡尔曼平滑是反向平滑滤波[7,20]。BCG信号先经过扩展卡尔曼正向滤波，滤除掉主要的噪声干扰，而后BCG信号再次通过扩展卡尔曼平滑滤波，对BCG信号反向平滑滤波，模糊其他因素的干扰。EKF+EKS复合滤波核心思想是将两种滤波方法组合起来，BCG信号先进行扩展卡尔曼滤波后，再进行扩展卡尔曼平滑滤波，滤波效果显著提高。联合扩展卡尔曼滤波与扩展卡尔曼平滑的复合滤波原理[22]如图3所示。

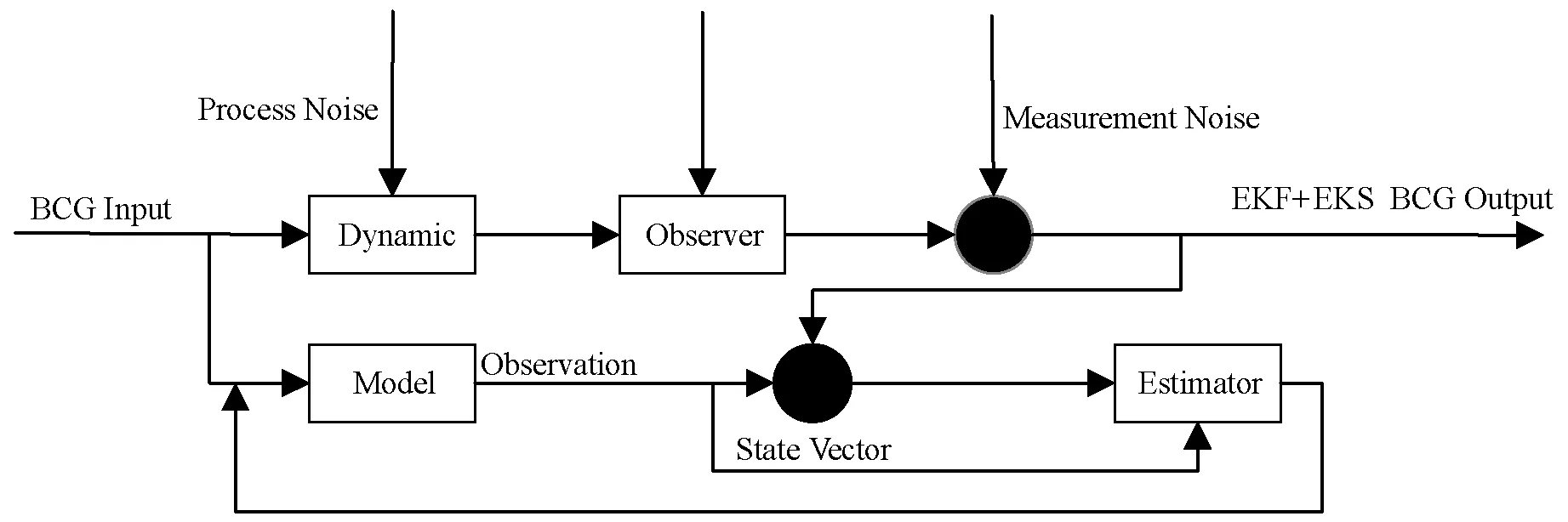
图3 EKF+EKS在BCG信号的处理

3 实验结果与讨论

3.1 BCG信号的经典滤波处理

压电薄膜传感器采集BCG信号的原始数据后，采用MATLAB数字滤波器进行信号经典滤波处理。经典滤波处理采用切比雪夫II型滤波器，切比雪夫II型3阶低通滤波器，阻带纹波30 dB，截止频率0.05 Hz，切比雪夫II型3阶高通滤波器，阻带纹纹波30 dB，截止频0.002 Hz，最后是采用数字陷波器去除50 Hz的工频干扰。图4所示为BCG采集的原始信号，图5为经典滤波处理后的BCG信号。

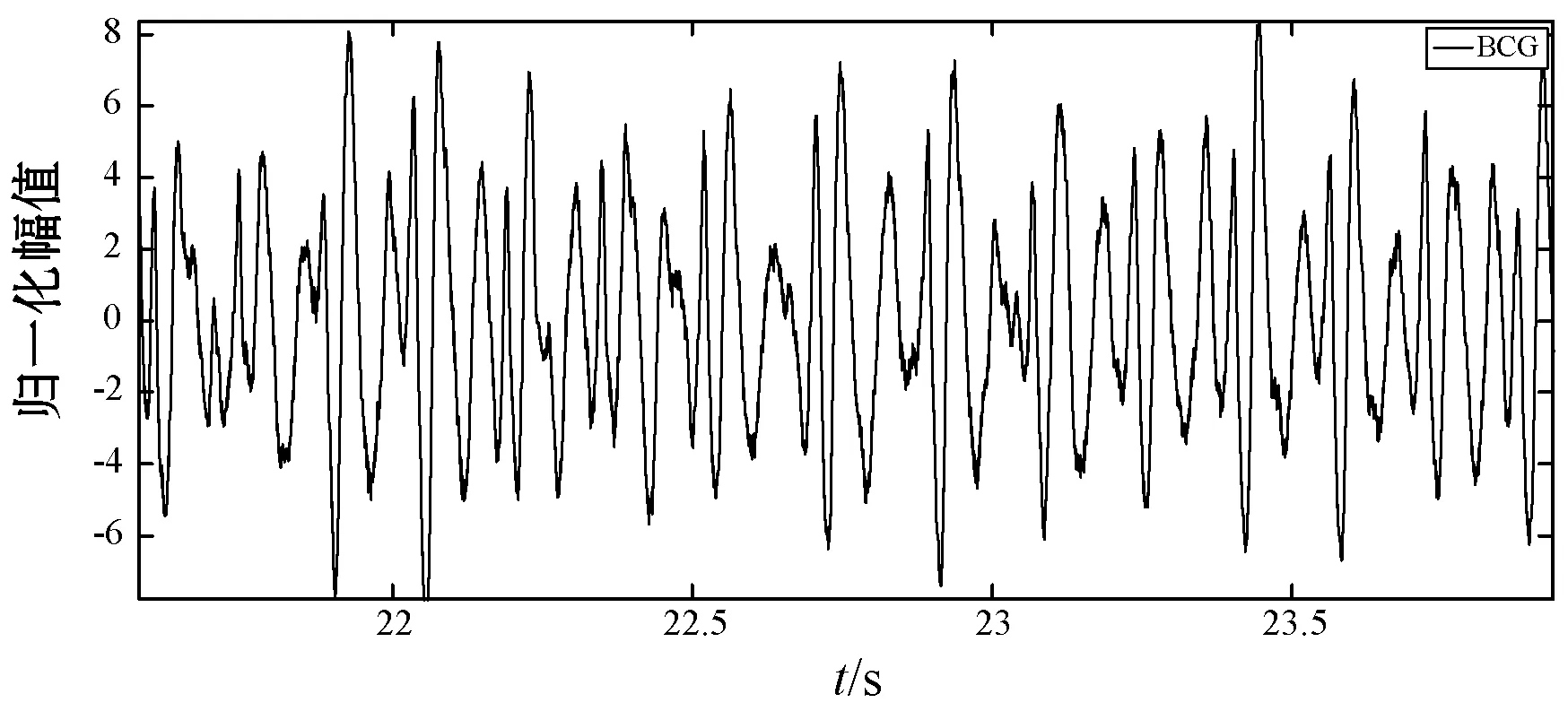
图4 BCG的原始信号

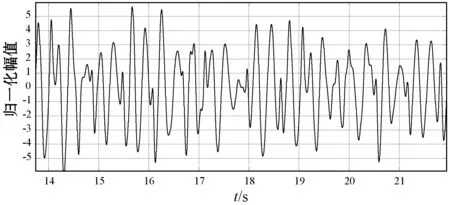
图5 经典滤波器处理后输出的BCG信号

3.2 动态高斯模型合成的BCG信号

本文提出的BCG动态高斯模型在笛卡尔坐标系生成一个单周期BCG信号的三维图像，如图6所示。在一个三维空间中，围绕着单位圆的轨迹显示BCG信号的准周期性质。轨迹的每一次循环表示一个心动周期的BCG信号。在x、y和z方向上的数值变化代表BCG波形的幅值变化。根据式(9)所描述的BCG动态高斯模型，利用BCG信号进曲线拟合与参数估计[23]，可以得到BCG波形中极大值和极小值点的动态高斯模型参数αi、bi和θi。表3所示为BCG信号的一组动态高斯模型参数值。

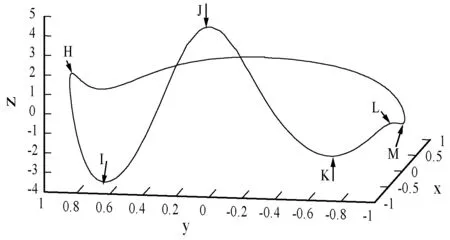
图6 单周期BCG信号三维展示

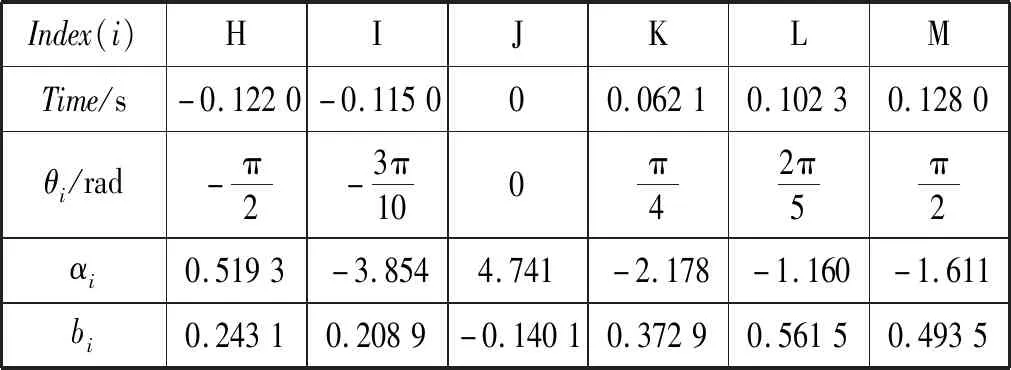
Index(i)HIJKLMTime/s-0.1220-0.115000.06210.10230.1280θi/rad-π2-3π100π42π5π2αi0.5193-3.8544.741-2.178-1.160-1.611bi0.24310.2089-0.14010.37290.56150.4935

类比推理，根据不同的高斯模型参数，可以相应地生成不同形态的BCG信号。为方便研究多周期的BCG信号，图6的三维空间展示可转换到二维空间展示，并加以周期延拓，形成多周期的合成BCG信号。

图7为单周期BCG信号，该模型合成BCG信号保留了H波、I波、J波、K波、L波和M波等特征，其周期延拓结果如图8所示。基于BCG信号的动态高斯模型，可根据需求，设置不同的模型参数，进而生成不同周期和不同形态的健康个体BCG信号。

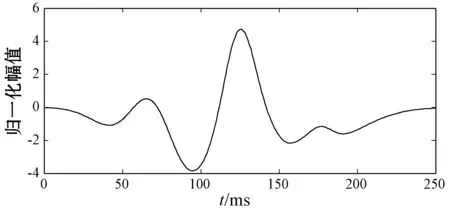
图7 动态高斯模型产生的单周期BCG信号

图8 模型产生的多周期BCG信号

3.3 模型生成的BCG信号与健康个体的信号比较

动态高斯模型合成的BCG信号属于无干扰、无噪声和幅值稳定的BCG信号。但通过包含压电薄膜的模拟电路采集的信号不能完全消除环境、设备和人为因素的干扰，因此动态高斯模型合成的BCG信号需人工添加一定比例的高斯白噪声，目的是为模拟健康个体产生的BCG信号动态高斯模型合成的BCG信号添加SNR=12 dB的噪声后的信号如图9所示。

图9 模型合成的BCG信号添加12 dB的高斯白噪声

虽然BCG信号属于非线性信号，但是每个周期的波形有规律性，BCG信号一个周期包含H波、I波、J波、K波、L波和M波等6个特征点，且特征点出现的先后顺序和幅值大小顺序保持不变。通过判断特征点的出现先后顺序、特征点的幅值大小顺序和信号走向趋势判断是否属于健康个体的BCG信号。由于模型的参数可以调节，可以产生不同形态不同周期的BCG信号。但无论何种形态的健康个体BCG信号的J波幅值最大和H波、I波、J波、K波、L波和M波出现先后不变。因此通过特征点的数量及其顺序和特征点幅值可判断动态高斯模型合成的BCG信号可替代健康个体产生的信号。图10为提取了该BCG信号的所有的特征点，并标识了所有周期BCG波形包含的6个特征，分别是H波、I波、J波、K波、L波、M波，且先后顺序和幅值大小一致。

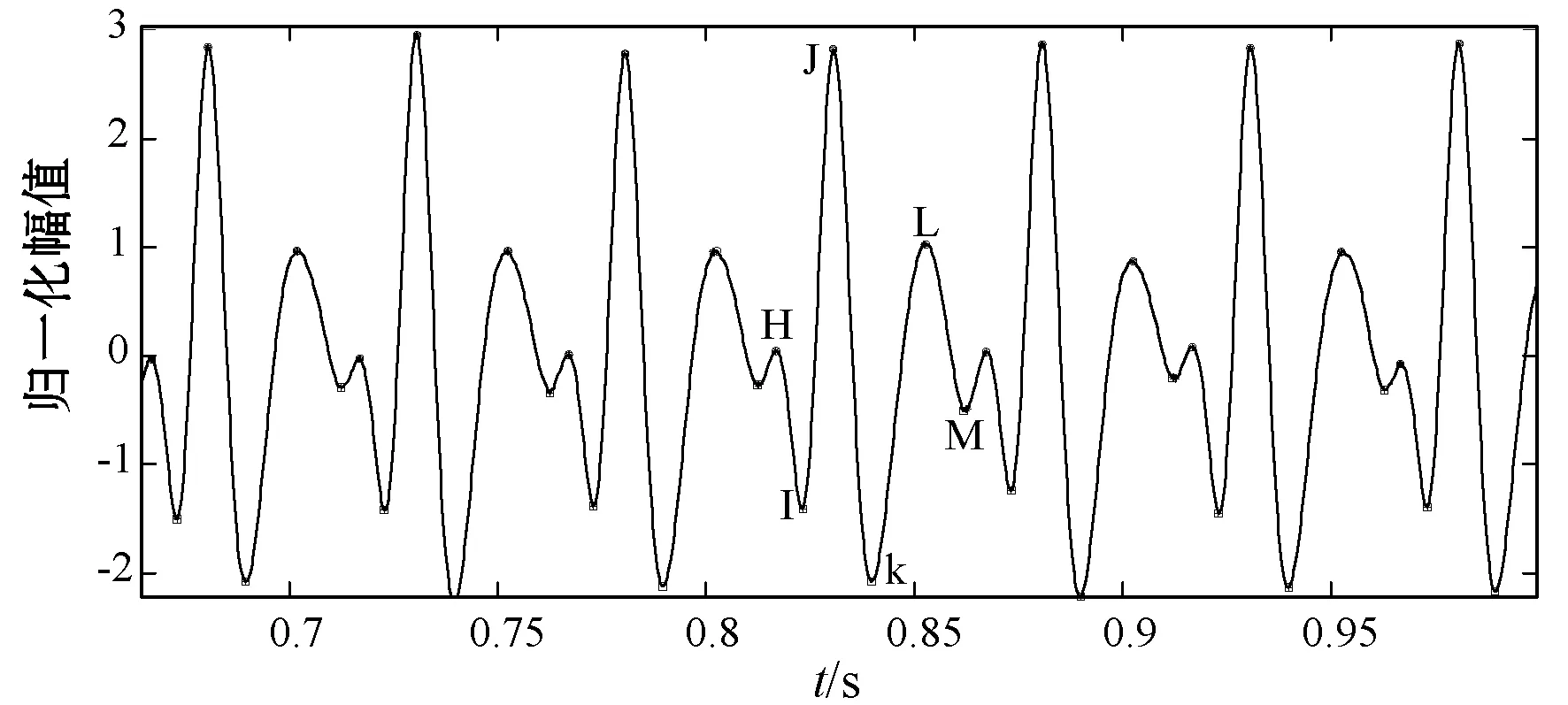
图10 模型合成的BCG信号特征点提取结果

健康个体采集的BCG信号如图11所示，与图9和图10比较后发现，模型合成的BCG信号保留了健康个体BCG信号的有效周期特征，动态高斯模型合成的BCG信号可替代健康个体产生的BCG信号[24]。

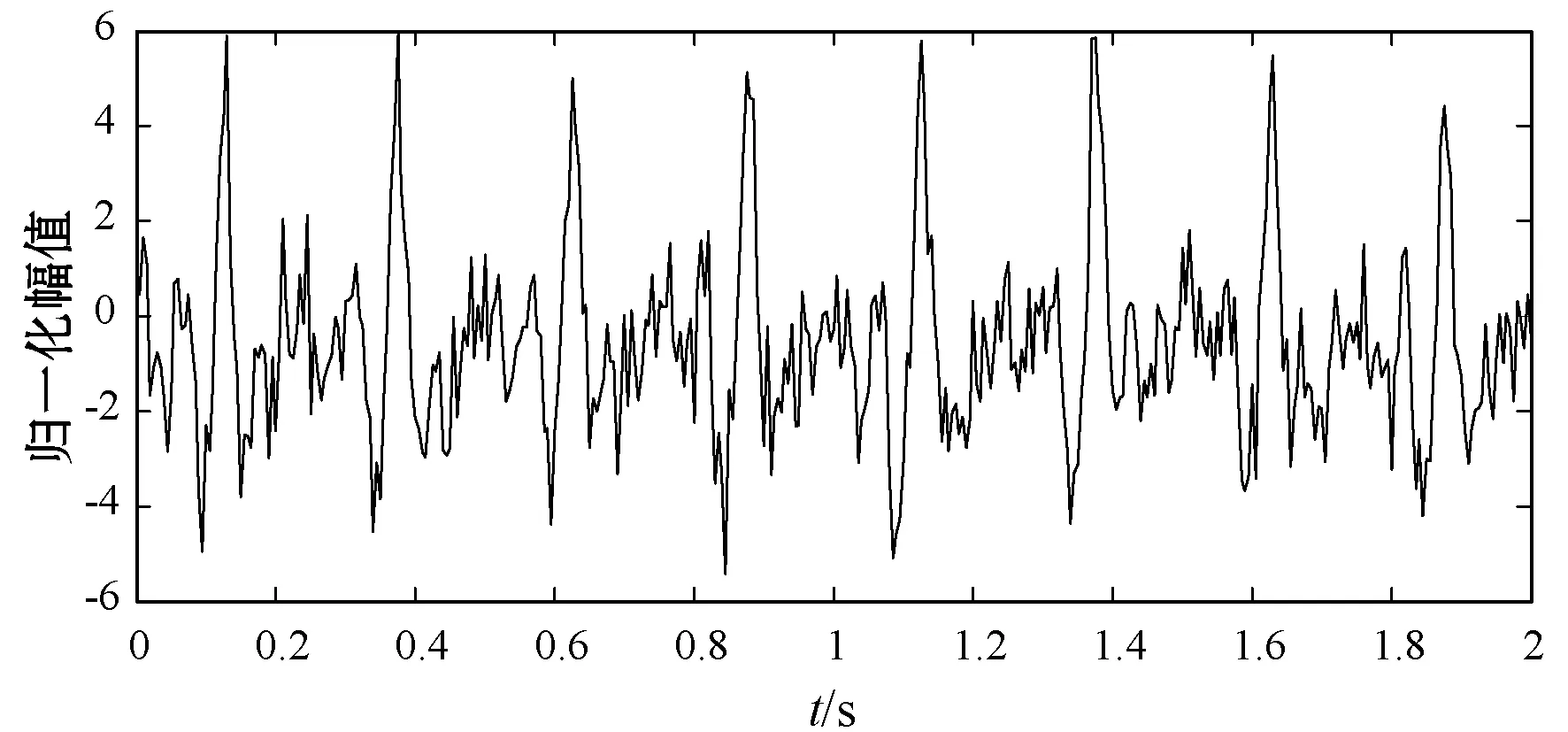
图11 健康个体采集的BCG信号

3.4 联合扩展卡尔曼滤波与扩展卡尔曼平滑复合滤波

本节的内容是对比不同滤波方法的降噪效果，信号的信噪比数值越大，说明信号的噪声越低，该方法的降噪效果越好。图12所示为向动态高斯模型合成的BCG信号中人工加入SNR=10 dB的高斯白噪声，图13所示为图12的信号经过经典滤波后的BCG信号，经典滤波由传统数字高通、低通和数字陷波器滤波组成。图13中BCG信号的信噪比为17 dB。图14所示为图12信号经过DB5小波进行6层分解处理后的结果，信噪比为16 dB。图15所示为图12信号经过EKF处理后的结果，信噪比为21 dB。图16所示为图12信号经过EKF+EKS处理后的结果，信噪比为22 dB。

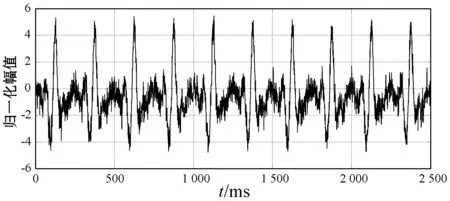
图12 向动态高斯模型合成的BCG信号中人工加入SNR=10 dB的高斯白噪声

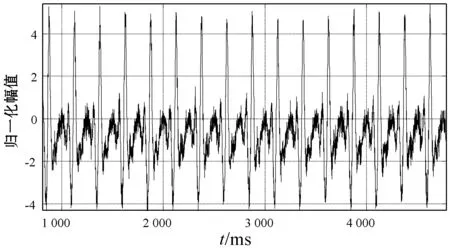
图13 经典滤波处理图12信号后的BCG信号

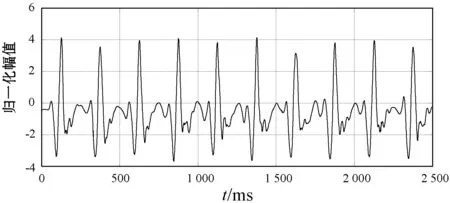
图14 经过小波DB5降噪处理图12信号后的BCG信号

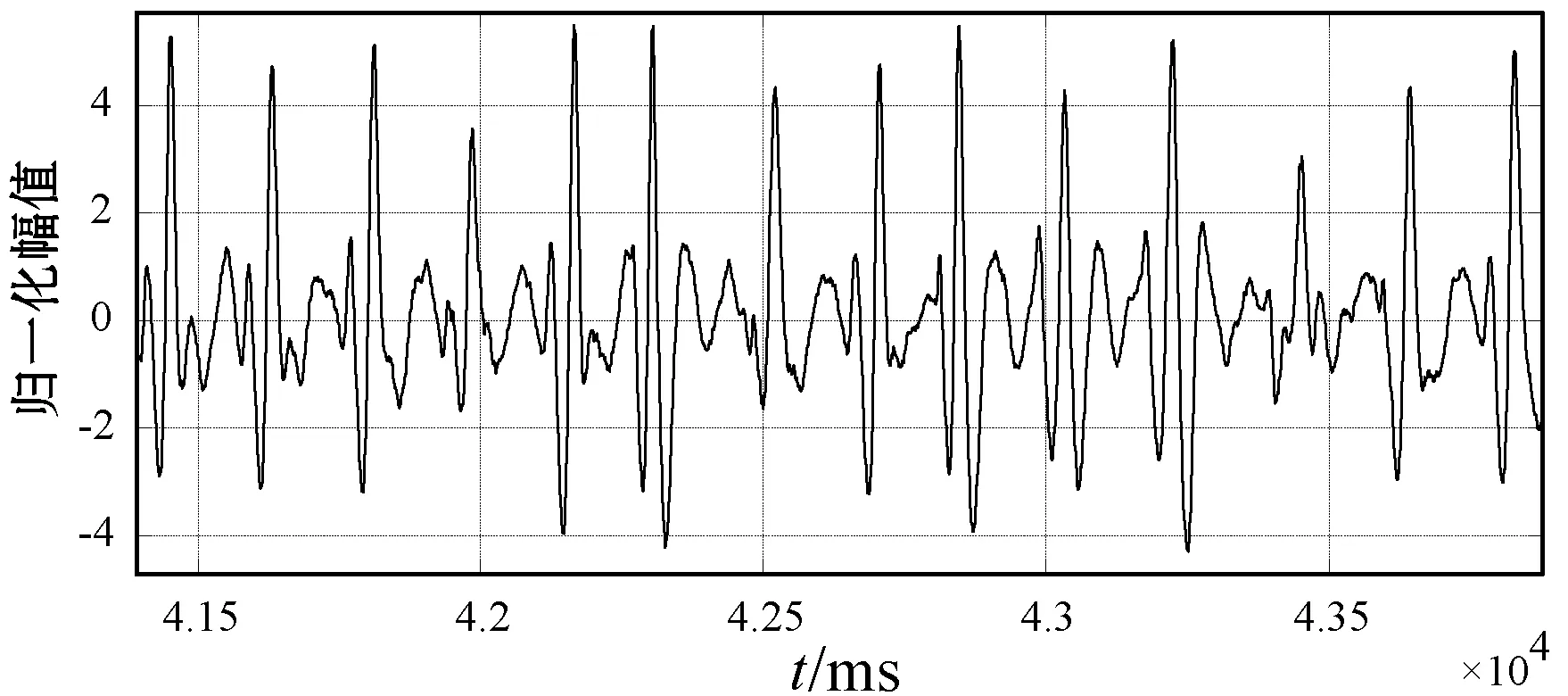
图15 经过EKF处理图12后的BCG信号

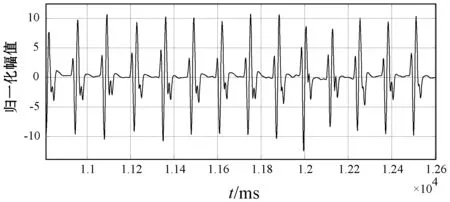
图16 经过EKF+EKS处理图12后的BCG信号

为了更好地比较不同方法的降噪的效果，我们对动态高斯模模型合成的BCG信号添加SNR数值范围为6～18 dB的等信噪比间隔的高斯白噪声，然后比较其滤波效果。

表4表明，具有相同信噪比的BCG信号通过代表4种不同方法的滤波器,分别是经典滤波器、DB5小波进行6尺度分解、EKF滤波和EKF+EKS复合滤波。通过滤波器后BCG信号的信噪比相比较,通过EKF+EKS的BCG信号的信噪比数值明显大于通过其他三种滤波器BCG信号的信噪比,证明针对BCG信号的滤波,基于EKS+EKF复合滤波效果比传统数字滤波降噪效果更好。

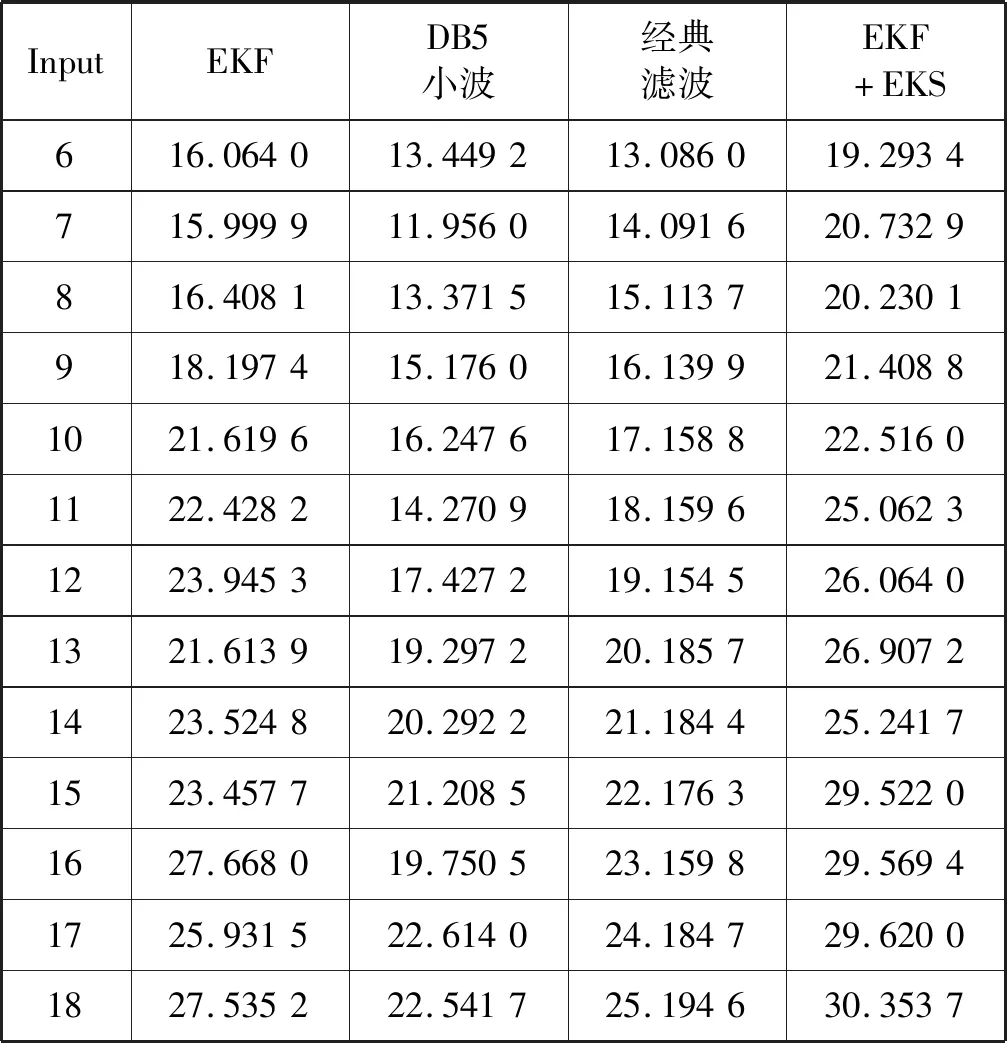
表4 不同滤波方法输出信号的信噪比 dB

4 结 语

通过理解动态ECG信号和PCG信号的动态高斯模型，本文实现了一种基于高斯核函数的BCG信号模型。通过设置不同的模型参数，可以生成不同形态和不同周期的BCG信号，包含H波、I波、J波、k波、L波和M波的特征。与健康个体产生的BCG信号比较后发现，动态高斯模型可替代健康个体合成的BCG信号。在动态高斯模型合成BCG信号的基础之上，运用了一种联合扩展卡尔曼滤波与扩展卡尔曼平滑的方法对BCG信号进行复合滤波，通过与经典滤波、扩展卡尔曼滤波和小波滤波后的信号信噪比值比较后发现，联合扩展卡尔曼滤波与扩展卡尔曼平滑复合滤波方法对BCG信号有更好的降噪效果。