通过对知识的变式生长来提高学习效率的研究

王荷凤

摘要：从一道例题或习题出发，对于书本的知识.氛，以学生为中心，以数学的发展为宗旨，立足知识和思维的生长点，保持已知条件不变，探索能否生长出更深刻的结论，或改变命题条件，生长组成新型的、逆向的、高一层次的命题;或改变图形位置与形状，改变题目的陈述，生长出一种“新情景”等，通过对变式题的研究、解决，形成完整的知识结构，培养学生举一反三，触类旁通的变通能力，促进知识的迁移。

关键词：变式生长;提高;学习效率

中图分类号：G623.5 文献标识码：A 文章编号：1672-1578（2019）01-0171-02

前言：教学过程中许多老师在不知不觉中应用了变式教学的方法或理念，但很少有老师对变式教学方法作深入的研究和剖析。变式生长教学法应用得最多的是在数学的教学中，典型的例子就是运用数学题目的一题多变，生长出新的知识，然后把书本上所学的各个分散的知识点串在了一起。具体来说，什么是变式生长教学法呢？就是老师通过有计划、有目标地对题目进行因果、已知未知、常量变量间的合理转换，以学生为中心，生长出新的知识，以数学的发展为宗旨，立足知识和思维的生长点，使得学生在解题过程中运用不同的知识点对题目进行求解。运用一题多变的方式，在潜移默化中将书本上所学的知识和方法有机结合在一起，进一步清晰了学生对有关概念、定理的理解和应用。引导学生在解题的过程中，通过自己的思考去发现数学中“变与不变”的本质，从变化的题目中找出不變的规律。变式生长教学法改变了传统教学中一味由老师传授的模式，变成了学生与老师在教学过程中互动的方式，或者学生要主动的，更有利于提高学生的解题效率和增强学习兴趣。

1.概念的变式生长引入

在数学的教学过程中，概念是根本，是学生解题的基础，让学生全面理解和掌握每一个概念是老师教学的关键。全面掌握概念的内涵和外延，对于学生解题来说能达到事半功倍的效果，更能激发学生的思考、总结能力，实现举一反三。传统的教学方法，老师们直接引入每一数学概念、定理，然后再逐点、逐条进行详细讲解，有时候遇上抽象点的概念，老师在台上讲得口干舌燥，学生也听得云里雾里。

而变式生长教学法则完全不一样，以学生为中心，以数学的发展为宗旨，立足概念的生长点，比如说：可以通过直观实物法生长法、类比生长法、情境生长法等进行概念的教学活动。

第一，直观实物生长法。例如：讲垂线时借助于教室里的黑板、墙角等学生们熟悉的直观物件，让学生一目了然理解两条线之间的垂直关系;也可以借助现代化的多媒体技术，把两条线的几种关系让学生生长出结论，让学生们建立起对两条线几种关系的直观感受。还可以和学生们一起互动通过搭建积木或物品的方式，让学生在思考、动手中学生长出两条线的垂直、平行等概念并理解运用这些关系，既学习的概念还紧紧抓住了学生的注意力，充分调动视觉、听觉、触觉等一起学习，更能提升学习兴趣。

第二，类比生长法。在教学活动中，遇到一些抽象的概念时我们可以用学生们较为熟悉的概念与抽象概念的比较来进行生长教学。从两个概念的相同或相似的地方人手，让学生渐渐认识抽象的概念。如：方程式与不等式、等腰三角形与全等三角等等。通过以旧引新的类比方式，让新的概念、新的定理更容易被学生认知、理解和运用。

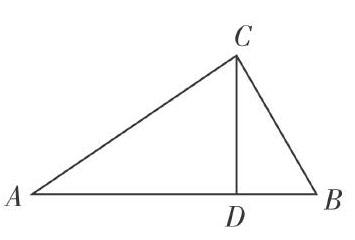
例：已知，ΔABC中，∠ACB=，CD⊥AB，D为垂足，求证：CD²=AD·CD。

上面这个例是书本的练习题，对相似性质的一个应用;然后我们可以对题目增加条件进行变式，以学生为中心，以数学的发展为宗旨，立足知识和思维的生长点，看学生是否对上题完全掌握;

变式1：已知，ΔABC中，∠ACB=，CD⊥AB，D为垂足，以CD为直径的圆交AC、BC于E、F，求证：CE：BC=CF：AC，

在原有的基础上，生长出一个圆，结论会如何？

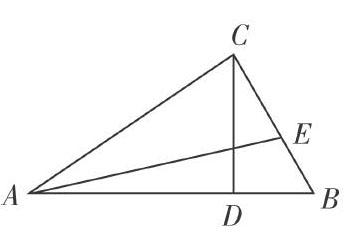
变式2：已知，ΔABC中，∠ACB=，CD⊥AB，D为垂足，AE平分∠BAC交BC于E，求证：CE：EB=CD：CB。

在原有的基础上，生长出一个角的平分线，结论会如何？生长出另一个角的平分线，结论又会如何？

变式3：已知，ΔABC中，∠ACB=，CD⊥AB，D为垂足，CF平分∠BCD，AE平分∠BAC交BC于E。

求证：（1）BF·CE=BE·DF。

（2）AE⊥CF。

（3）设AE与CD交于Q，则FQ//BC。

在解决繁多的数学题目中，我们有必要提倡以“一题多变”的方式教学，从“变”中总结解题方法，从“变”中发现解题规律，从“变”中发现“不变”，引导学生多思多想，养成在学中求异，学中求变的习惯，使学生学习一道题，学会一类题，加深对问题实质的理解和掌握，增强应变能力，构建知识的条理性和系统性，从而培养学生的探索精神和创造性才能。

第三，情境生长法。情境生长法就是以人为本的教学方法以，即：为学生的学习为中心，策划更多的动手的情境融会在教学过程中。这一教学方法尤其用在几何图形及知识的学习中效果最佳。课前让学生准备到一些纸片，教学过程中老师带着学生一起动手，把准备好的纸片折成需要的形状，然后再展开成平面图，学习对认识几何图形的对角线、边、垂线、角等相关概念就比传统的老师在黑板上画图要形象、生动得多，更利于学生们对抽象概念的掌握。同时，通过学生物业自己动手，为学生们也提供了一种解题的方法，通过观察、探索、分析和总结，让学生在乐趣中学习，更容易生长出新知识。

例：如下图所示：AB//CD//EF，那么∠BAC+∠ACE+∠CEF=？

A.1800 B.2700 C.3600 D.5400

围绕运用平行可以将此题作几种变式：（1）AB//EF，试探求：∠BAC，∠ACE，∠CEF之间的数量关系;（2）AB//EF，试探求：∠BAC，∠ACE，∠CEF之间的数量关系.（3）AB// EF，试探求：∠BAC，∠ACE，∠CEF之间的数量关系。

2.思维方式方法的变式生长

如何提高学生的解题效率呢？这个问题不仅是每一名老师关心的问题，更是学生们迫切想解决的问题。传统的教学模式下，老师教学生学，学了书本的知识大多数老师就会选择让学生做“成千上万”的题目，就想让学生把所有相关的题目类型都做到、都会做。这种方法在几年前或者说几十年前，学生的学习范围、知识面相对不多的情况下，不能不说是一个好办法。而如今我们已进入新时代，知识量爆炸增长，学生们要学习的新知识越来越多，而每个学生的时间和精力始终和以前一样都是有限的。现在的学生常郴会说一句话“题目是永远也做不完的”，显然要继续用“题海战术”来提高学生的解题效率，一方面是老师一个人在有限的时間内也不可能收集到所有类型的题目;另一方面，学生也无法做尽所有类型的题目。

例如：在解一元二次方程x²-3x-4=0时，同样的问题可以变式为：

变式1：你能结合二次函数图象求出x²-3x-4>0的x取值范围吗？

变式2：际能结合二次函数图象求出x²-3x-4<0的x取值范围吗？

变式生长教学法提倡以人为本的学习理念，不把学生当成“机器”，而是有思考、总结能力的“人”。变式生长教学理念强调的是把书本上所学的知识转变成学生的能力，实现高效解题的目标。通过一题多变的思路，一次性把一类型的问题解决，并相关的知识点联系在一起形成体系。变式生长教学理念中最关键的就是在教与学的过程中，充分发挥学生学习的主动性，强调思考总结与探索，生长出更多更好的知识。思考对于学习来说是一个必不可少的关键环节，尤其对于提高学生的解题效率来说，思考远远比做更多的题目重要。学生通过举一反三、一题多变、转换因果等方式对一道题进行深入的分析、思考可以获得解题的思路和方法，逐渐形成为自己解题的能力。万变不离其宗，只要学生把概念、定理这些知识变成了自身的能力，无论遇上什么样的题目，解题的效率自然就会很高。

结语：众多的教学表明，适应学生的认知、心理的教学方法才是最有效提高学生解题效率的教学方法。教学过程，在吃透概念的基础上一定要让学生积极思考、归纳和总结书本的知识点，以学生为中心，以数学的发展为宗旨，立足知识和思维的生长点，生长出更多的知识，才能提高学生的能力。

参考文献：

[1]文林.数学史概论（第三版）[M].北京：高等教育出版社，2011：41-44.

[2]存娣.用解析法求解“PhiloS Line”[J].西安工业学院学报，1992，2：78-82.

[3]黄坪（1998）.一题多解问题的解法特性与思维训练.数学通报，1998（7），pp.22-24.

[4]刘健（2003）.谈变式教学中习题引申应注意的几个问题.数学通报，2003（1），pp.30-31.