“同心协力”数学建模设计及研究

徐文轩 刘焱

摘 要：“同心协力”是一项团队协作能力拓展项目。该项目以团队各人员用绳牵拉同心鼓颠球，通过合格的颠球数量比拼。本文综合数学与物理学知识建立了二阶微分方程组的数学模型，来分析如何更多的颠球和即时调整，最终对模型的结果做出了误差分析

关键词：牛顿第二定律;二阶微分方程组;刚体转动定律;控制变量法

一、前言

“同心协力”活动是以团队协作能力为核心的拓展活动，该活动是以团队各人员用绳牵拉同心鼓颠球的过程，同心鼓的转动可以等效为刚体的转动，则可计算鼓的转动惯量，然后给八人均分站位，根据其给出的数据计算出倾角大小。再以球与鼓的接触点为坐标原点，分别以球、鼓为研究对象求出若干分钟后稳定状态下球下落（鼓上升）的时间、人拉绳所产生的合外力和最佳颠球高度。因此对鼓上力的大小，发力时机，颠球高度和所用的时间的细化计算尤为重要。

二、颠球高度、时间和鼓转动倾角的理论分析

2.1模型假设

①假设球与鼓接触时恰巧绳拉直②忽略自然风产生的外力和球与鼓接触时产生的摩擦力③球与鼓接触时发生弹性形变所产生间隔和时间忽略不计④不考虑能量损耗 ⑤若干分钟后球（>=40cm）保持平稳状态。

2.2问题一模型建立

利用牛顿第二定律建立一阶非线性微分方程模型，分别以球、鼓为研究对象求出若干分钟后稳定状态的球下落（鼓上升）的时间、人拉绳所产生的合外力和最佳颠球高度。

本文以竖直向下为正方向，建直角坐标系，已知球下落的时间与鼓上升的时间相同。以“球在空气中运动”的状态将常数取值，则取空气密度（20℃时）。垂直下落的球受到重力G、空气浮力和空气黏滞阻力三个力的作用，其中m M分别为球和鼓的质量，V为球的体积，为空气阻力系数，分别为球和鼓的最大横截面积，分别为球和鼓相对于空气的速度。但是在计算过程中，我们求得空气浮力约为N可忽略不计。

2.3 问题一模型计算

我们根据牛顿第二定律分别列出排球和鼓的微分方程：

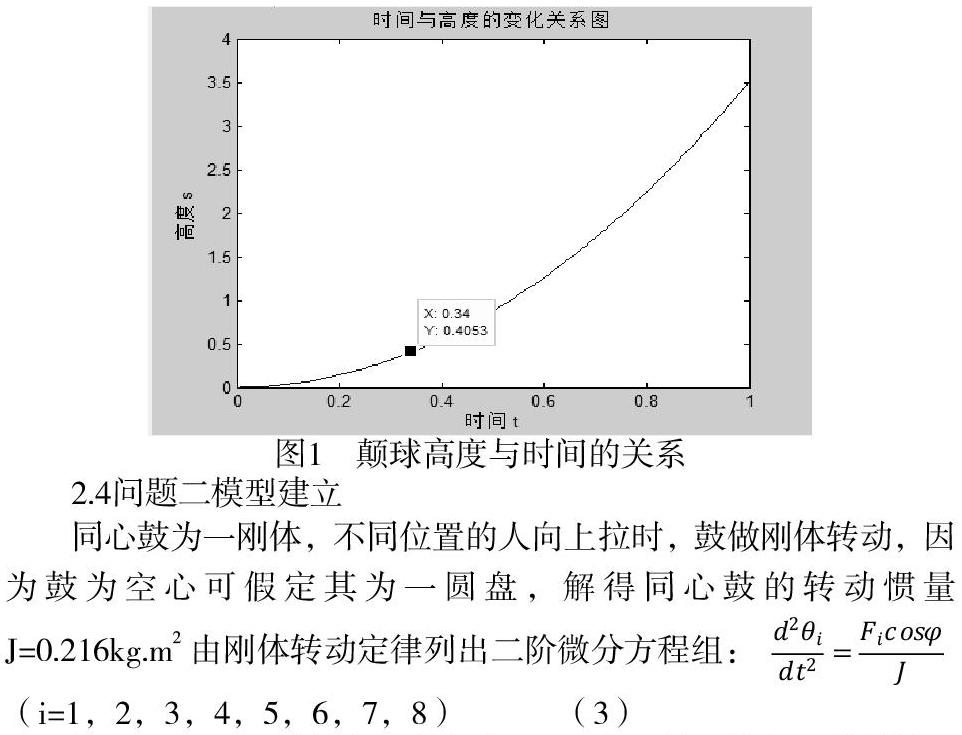
根据题 “可以精确控制用力方向、时机和力度”的要求，对鼓的合外力设为45N，求得鼓位移函数为：S1与S2。利用MATLAB画出图1

如图当s时符合“颠球高度0.4m以上”的要求。且“颠球次数尽可能多”则需要颠球一次所用时间越短，在相同时间内累计颠球次数就越多，所以取0.34s为一次颠球所用时间，则此时高度m。

2.4问题二模型建立

同心鼓为一刚体，不同位置的人向上拉时，鼓做刚体转动，因为鼓为空心可假定其为一圆盘，解得同心鼓的转动惯量J=0.216kg.m2由刚体转动定律列出二階微分方程组：（i=1，2，3，4，5，6，7，8） （3）

该方程组用于研究队员发力时机、力度和某一特定时刻的鼓面倾斜角度的关系，其中变化很小，近似当做恒定值。

根据上式求得九组鼓面倾角分别为：0.6939、0.484959、1.08711、0.86352、1.14108、0.937536、0.925118、1.013865、0.461058。

在计算过程中，我们求得空气浮力对模型影响很小，故该因素忽略不计

三、模型检验

以排球为研究对象，在理想状态下忽略空气阻力，排球做自由落体运动时所用时间为s，所以与实际相符。

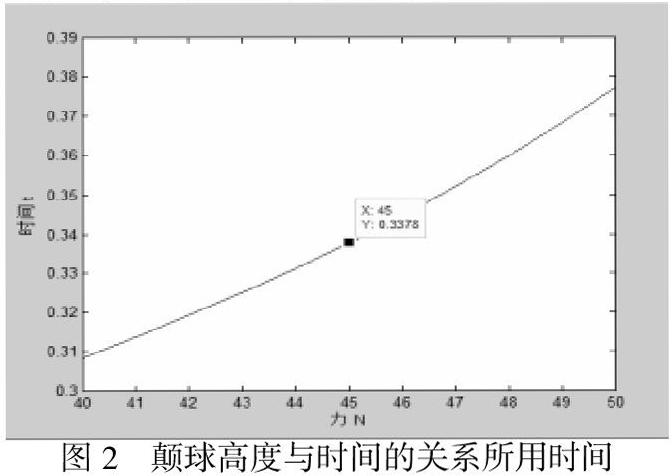
本文给合外力赋值，利用MATLAB画出与的变化关系如下图2，由图知F=45N时 0.3378≈0.343s。因此本文根据一阶非线性方程模型求得的t=0.34s是合理的。

四、总结

承接以上问题，抛去所需的理想状态，在现实情形中计算颠球时间和高度策略不再合适，因此根据人的发力时机、发力大小对模型的影响建立新的策略模型，使之更符合现实情形。而对于这方面的深入研究还需要进一步完善。

参考文献：

[1] 司守奎，孙兆亮，数学建模算法与应用，北京：国防工业出版社，2018.9。

[2] 鞠衍清，垂直下落球体运动的数值分析，大学物理，第27卷第11期。

作者简介：徐文轩，男，汉族，新疆省塔城市，1999，3，大学本科，机械设计制造及自动化专业;

刘焱，女，汉族，研究生，讲师，研究方向：数学建模。

（作者单位：山东协和学院）