基于GARCH-VAR模型的创业板指数收益率波动特征比较研究

赵鹏举 海洋 殷燕

摘要：本文使用GARCH-VAR模型分别在正态分布、t分布和GED分布的情况下研究比较创业板和主板的波动特征及市场风险，结果表明GARCH模型在t分布和GED分布能够更有效的反映收益率的尖峰厚尾特征，正态分布和GED分布下的在险价值度量相对可靠。综合起来考虑，使用GED分布来刻画创业板市场的收益率特征及在险价值效果最好。所有检验结果均表明创业板比主板具有更大的风险，同时也具有更高的回报率。

Abstract： This paper aims to measure and compare the market volatility and risks between Chinese growth enterprise market and main board market under three different distributions based on GARCH model. The results illustrate that， t-distribution and GED distribution are the most efficient patterns to depict the characteristics of volatility. The results also show that VaRs under normal and GED distributions are more reliable than t-distribution，moreover， all of the tests proved that the risk of the growth enterprise market is far more than that of the main board market， and at the same time has a higher rate of return.

关键词：GARCH模型;在险价值;创业板;价格波动

Key words： GARCH model;VaR;growth enterprise market;volatility

中图分类号：F830.91                                     文献标识码：A                                  文章编号：1006-4311（2019）25-0005-05

0  引言

科技型中小企业是我国实现创新型国家战略的一支重要力量，科技型中小企业的融资需求直接决定了科技型中小企业能否发展壮大。为满足科技型中小企业的融资需求，我国目前已经逐渐构筑起了多层次的金融市场，对科技型中小企业的支持力度也在逐年加大。其中创业板市场在其中起到了愈来愈重要的作用。

我国创业板市场成立年限较短，市场的广度和深度，市场流动性、市场稳定性等各方面指标都与发达国家有较大差距。同时，相较我国主板市场，我国创业板市场也存在着交易不够活跃，市场波动性高等一系列问题。这些问题严重影响了创业板市场吸引资金的能力，制约了科技型企业的发展，进而影响到我国创新型国家战略的实现。

市场波动率和市场风险是衡量市场稳定性的关键指标，对我国创业板市场的波动性进行研究有助于提升市场效率、增加市场对投资者的吸引力。本文以我国创业板市场为研究对象，选取科技型中小企业样本对我国创业板市场的资产收益波动性特征及风险特征进行了研究。比较了不同分布情况下创业板市场和主板市场的波动特征和市场风险，并提出了意见和对策。

1  文献综述

20世纪90年代，由于国际上大范围爆发金融危机，风险管理受到了前所未有的重视。在此之前，对于风险的度量一直依赖于Markowitz（1952）的均值-方差模型，用期望收益和期望方差之间的平衡来衡量投资的不确定性。Sharp（1964）通过对投资组合理论的衍生研究提出了建立在方差所衡量的系统风险和贝塔系数所衡量的非系统性风险上的CAPM模型。以上建立在方差之上的模型虽然给风险的测度提供了可以量化的指标，但是也具有一定的局限性。Arrow（1965）在研究风险厌恶函数时提到，方差作为风险度量工具来衡量不确定性是不恰当的，因为现实中投资者衡量风险时在效用函数中通常给低于头寸的投资结果给予更大的风险权重，反之权重较小，所以实际上的收益率一般是偏斜的，而方差所衡量的风险比重是一致的，不符合實际。因此Morgan（1995）提供的VaR（Value at Risk）方法克服了方差的局限性，用投资者的最大可能性损失来衡量风险的大小，结果更为直观可靠。我们将采用此方法衡量和对比创业板的市场风险。

VaR是金融产品在a%的置信度水平下的最大可能性损失。每日的在险价值其中N-1为累计正态分布函数的反函数，σ为收益率的标准差，μ是收益率的均值。为了更加便于和资产收益率进行直接对比，我们在下文计算VaR时，将上述公式转化为：此时该在险价值可以理解为：在a%的置信水平下所预测的最小可能性收益率。由于VaR方法依赖样本的分布函数，因此我们必须在使用此方法时必须首先确定股票收益率的分布函数。对资产收益的分布假设是研究金融市场和分析市场风险的前提和基础。多年来的一系列研究（Fama，1965;Cont和Bouchaud，2000;吴冲锋等，2000;赵鹏举，2009）表明，股票收益率的分布比正态分布的钟型分布尾部更厚，峰度更高。此外，股价的波动还具有聚集性，Engle（1982）提出了刻画股价波动聚集性的模型。Bollerslev （1986）在Engle提出的ARCH模型的基础上，在均值方程中加入了方差本身，从而可以用来更加方便精简的刻画高阶的ARCH现象，即GARCH模型族的起源。近年来，运用GARCH模型解决资产收益的波动问题得到了普遍的认可（Glosten，et al，1993;Herwartz，2017）。

前面所说的GARCH族模型都是用来衡量收益率的波动性特征的，也就是方差的特征。我们就在GARCH族模型均值方程和条件方差方程的基础上预测出时间序列的均值和方差，然后代入上述在险价值VaR的方程即可得每日的在险价值。

VaR方法假定，在市场正常波动的基础上计算金融市场所面临的最大风险，是在假定正态分布的市场环境中计算出来的，这意味着不考虑其他极端条件发生的概率，假定收益率服从正态分布。但系列研究表明正态分布假定并不符合现实。吴俊（2015）通过构建ARMA-GARCH族模型，对比发现GED（广义误差分布， Generalized error distribution）分布较t分布更好拟合拆放利差序列尖峰厚尾特征。本文计算GARCH模型时的分别将正态分布，t分布和GED分布的情况都加以考虑，计算出不同分布下的条件方差，然后在计算VaR时将修改后的适应新分布的分位点代入模型中去计算在不同分布下的在险价值。随后对不同的分布假定进行对比分析，寻找最优的分布假定。

2  实证分析

2.1 数据说明

本文数据来源于CSMAR数据库，选取深圳证券交易所2010年6月1日至2018年4月11日创业板股票收益指数日数据，共计1910个交易日数据，用R表示。收益率定义为连续复利收益率： ，计算后共计得到1909个对数日收益率数值。同时，为进行对比分析，我们选取相同日期的深成指作为主板收益率的代表，将中小板收益率和深成指收益率做相同的检验，深成指主板收益率用Rshen表示，定义为： 。

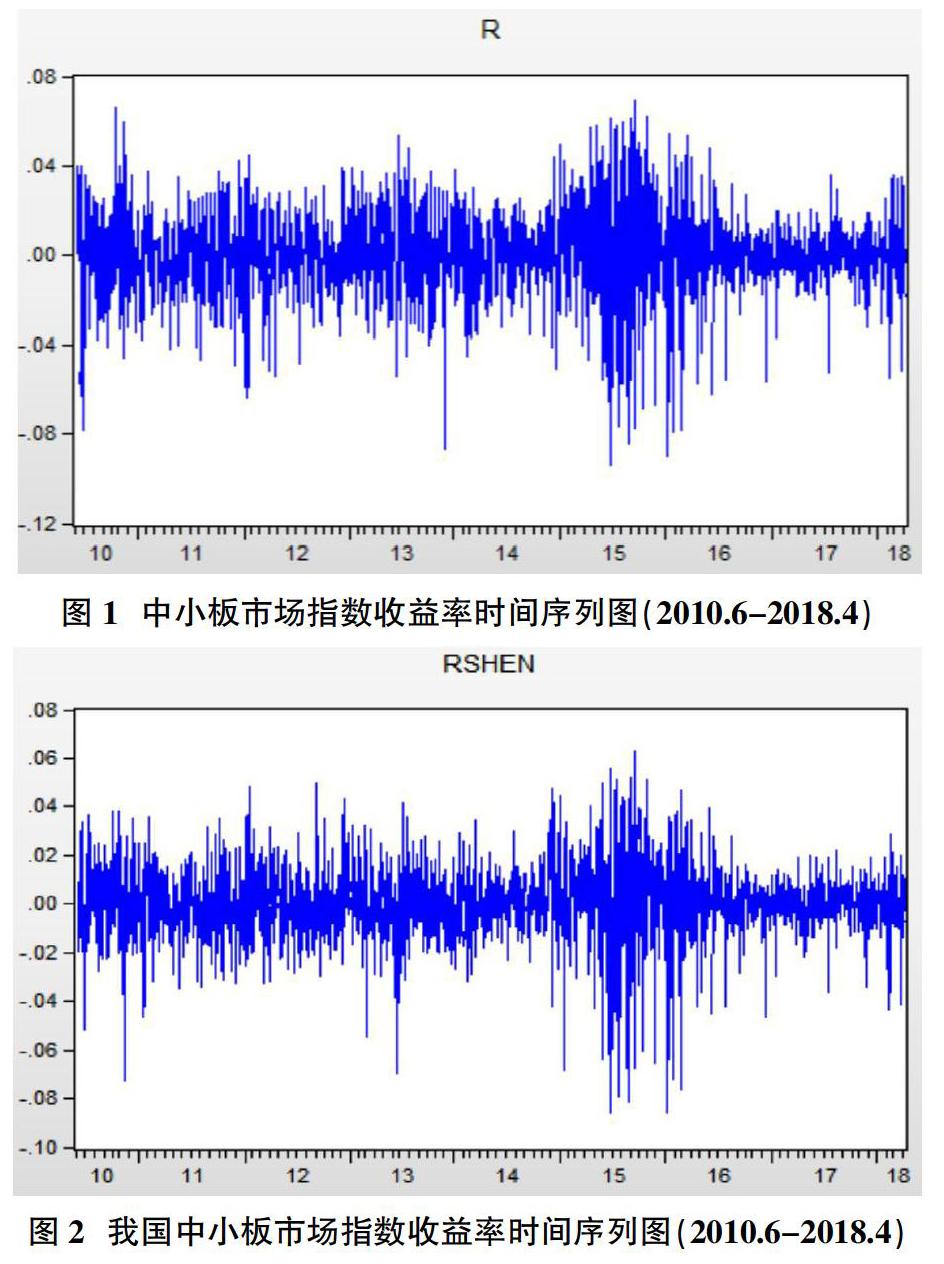
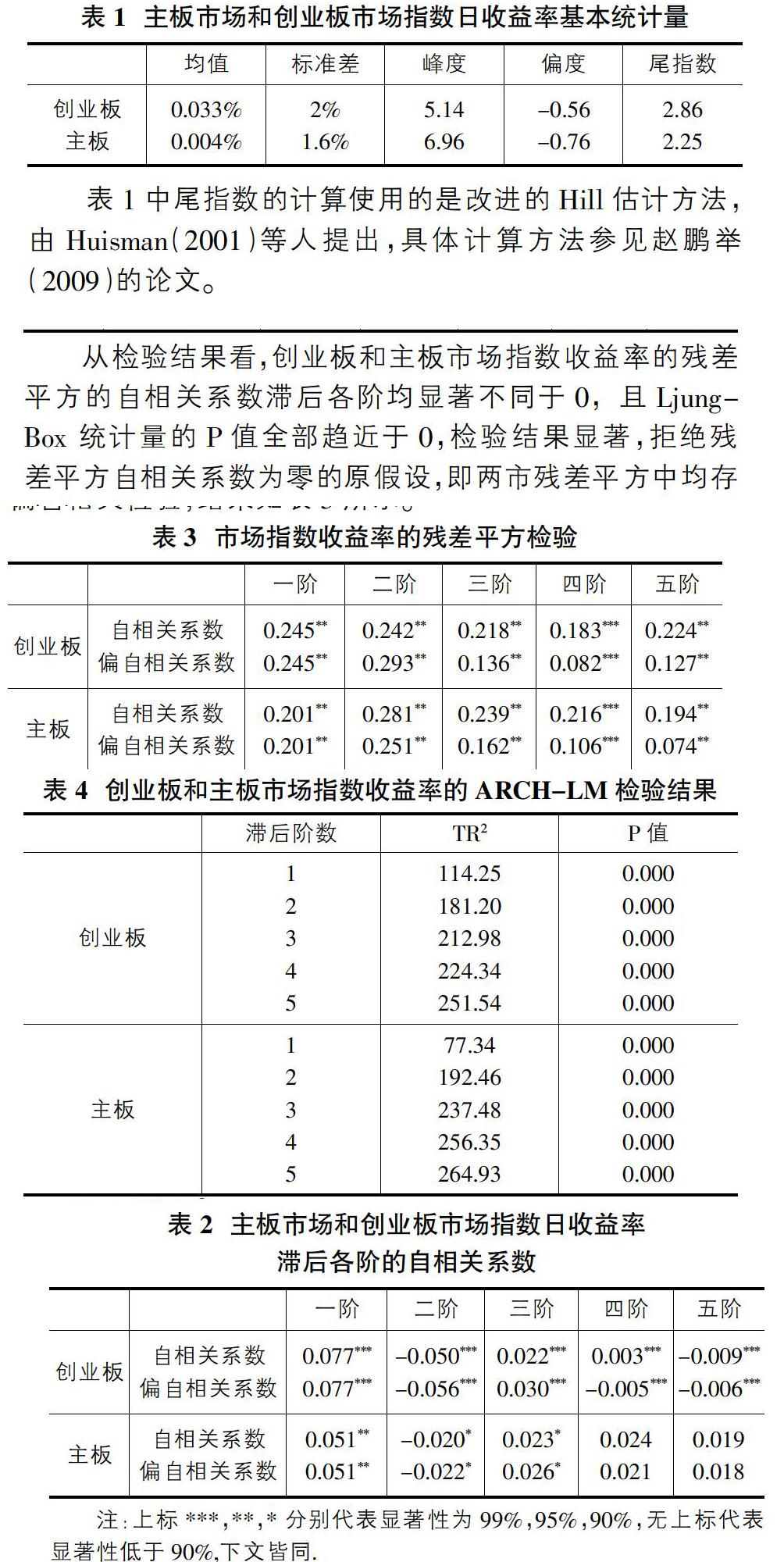
图1和图2分别描绘了中小板市场和主板的指数收益率波动状况。

从创业板市场和主板市场指数的收益率时间序列图中，可观察到二者均存在波动“集聚”现象，因而使用ARCH族模型刻画。除波动集聚现象外，两市指数收益率分布还表现出明显的尖峰厚尾现象，而且偏度为负。表1汇总了两市收益率的基本统计特征。

表1中尾指数的计算使用的是改进的Hill估计方法，由Huisman（2001）等人提出，具体计算方法参见赵鹏举（2009）的论文。

从表1中可以看出，主板市场收益率较低，同时风险较小，两市指数日收益率都具有明显的尖峰厚尾现象，Jarque-Bera统计量分别为461.9和1426.6，P值均接近0，拒绝服从正态分布的原假设。而创业板市场的厚尾现象更显著，表明创业板市场极端收益发生的概率更大。兩市收益率偏度均为负值，表明低收益率发生的概率较大，这一点主板市场表现的更为明显。

下面我们在GARCH族模型的基础上更符合收益率波动尖峰后尾特征的t分布以及GED分布下的两个板块指数日收益率的在险价值VaR。

2.2 数据模型

模型的基本思路是首先选取恰当的GARCH模型来刻画市场收益时间序列的均值和方差特征，随后用GARCH模型计算出指数收益率的条件方差，其后开方求出标准差，使用该标准差使用VaR模型对中小板市场和主板市场的市场风险进行对比分析。

2.2.1 数据平稳性检验

我们对创业板和主板的指数收益率时间序列分别进行单位根检验，ADF检验结果的t统计量分别为-40.4159和-41.4995，P值为0，结果显著，创业板市场和主板市场的指数收益率均为平稳序列。

2.2.2 收益率序列的自相关性检验

分别对主板和创业板收益率进行自相关性检验，结果如表2所示。

从表2中可以看出，创业板几乎各阶的滞后项超出误差边界，P值显示统计结果非常显著，均在99%的置信水平下存在自相关;主板在滞后一阶、二阶和三存在自相关，而第三至七阶自相关性不显著。因此，创业板和主板均能显著拒绝序列不存在自相关的原假设，序列存在自相关。

2.2.3 检验残差ARCH效应

为了初步断定残差序列是否存在ARCH效应，我们提取扰动项，并分别对创业板和主板收益率建立一个只包含常数和扰动项的简单方程， 和 ，利用简单OLS法进行回归，回归结果中常数项的t值分别为0.71和0.09，p值0.48和0.92，不能拒绝参数为0原假设。回归方程拟合为 和 。我们可以初步认为对数收益率符合随机游走。提取误差项，进行关于残差平方 和 的自相关和偏自相关检验，结果如表3所示。

从检验结果看，创业板和主板市场指数收益率的残差平方的自相关系数滞后各阶均显著不同于0，且Ljung-Box 统计量的P值全部趋近于0，检验结果显著，拒绝残差平方自相关系数为零的原假设，即两市残差平方中均存在自相关。

为了检验残差序列是否存在自相关的条件异方差，我们通过更正式的拉埃格朗日原理（LM）来检验ARCH效应。建立以残差滞后项为残差平方的函数的辅助方程：检验结果见表4。

从表中可以看出，直至残差滞后项5期，我们可以观测到两个序列的TR2值都很大，而且随着滞后项增多而逐渐增大，P值趋向于0，表明因变量被自变量解释的比例很大，且原假设出现概率极低，因此拒绝残差序列中不存在ARCH效应的原假设，两市指数收益率序列的残差序列均存在ARCH效应。

2.2.4 建立GARCH模型

由于上述检验证明序列R存在序列自相关，且通过回归残差自相关图判断采取AR模型较为适合。所以我们采取AR模型来描述均值方程。根据拟合结果的AR滞后项z统计量和p值来看，创业板序列的AR（3）、AR（4）、AR（5）以及常数项均不显著，所以将这四项从均值方程中剔除。主板序列除AR（1）之外的项均不显著，我们在均值方程中保留AR（1）其他部分剔除后进行下一轮拟合，结果如表5。

对两市的残差平方序列检验结果发现，残差平方中存在高阶的自相关的条件异方差。总结上述检验发现，AR（2），GARCH（1，1）模型能够较好的描述创业板收益率的波动性特征;AR（1），GARCH（1，1）模型能够较好的描述主板收益率的波动性特征。最终选定的模型如下：

创业板市场的GARCH模型：

主板市场的GARCH模型：

两市指数收益率的GARCH模型在不同的分布假定下分别进行拟合，其相关参数见表7。在上述检验结果的基础上，我们对模型拟合的优良性进行最小信息准则检验。不同分布下的GARCH模型拟合检验结果如表6所示。

从检验结果可以看出，三种分布假定下模型拟合的优良性质相差微乎其微，相对而言，无论是对于创业板还是主板来说，t分布和GED分布都比正态分布下的AIC和SC值要小，其中t分布下的值最小。说明t分布和GED分布相比正态分布更能准确刻画收益率的波动性特征。

3  基于多分布下GARCH-VaR的比较实证研究

在前文检验的基础上，我们分别使用三种分布假设（正态分布，t分布，GED分布）来对比讨论创业板及主板在GARCH模型下的在险价值。

3.1 三种分布下的波动性特征分析

在前文所述检验结果的基础上，对创业板和主板市场指数收益率的GARCH模型分别进行回归，结果如表7。

从上述检验结果可以看出，创业板方差方程中的所有ARCH项和GARCH项都是显著异于0的，且参数之和小于1，满足参数的约束条件。由于系数之和接近于1，表明条件方差的收敛速度较慢，所受到的冲击σ具有持久性。另外模型回归的对数似然值较高，模型具有可信度。

主板数据在三种分布下的GARCH模型方差方程中的所有ARCH项和GARCH项也都是显著异于0的，且参数之和小于1，但是小于创业板的参数之和，证明主板条件方差收敛速度比创业板快，一个方差所受到的到冲击不如创业板的持久。

3.2 三种分布下的在险价值比较

GARCH模型在三种分布假设下的95%置信水平和99%置信水平的创业板股市的在险价值VaR，基本统计量分别如表8。

相对于主板市场，在三种分布的两种置信度水平下，创业板的在险价值最大值和最小值都比创业板要高，均值和标准差也都更高，说明创业板的波动幅度比主板要大，创业板的最大可能性损失高于主板，投资风险比主板要大。

相对于正态分布假定，在t分布下，GARCH族模型所衡量创业板的收益率的在险价值覆盖范围均有所扩大，最大可能性损失的值域更加宽泛，均值和标准差都有所提升。这意味着在t分布下，我们所捕捉到的创业板的市場收益率波动比正态分布下预测到的波动剧烈，捕捉到的极端情况相对要多，估测到的风险较正态分布下的风险要大。

GED分布下捕捉到的收益率波动风险在三种分布中处于居中，比正态分布下估测到的风险高，但是低于t分布下估测的风险值。

3.3 三种分布下的失败频率对比分析

为了检测创业板每日的价格波动是否在期望风险范围内，验证三种分布情况下的GARCH模型所衡量的在险价值能否精确有效反映创业板投资风险，我们在GARCH模型的基础上对创业板日收益率、主板日收益率的在险价值分别在两个置信度水平下进行了计算并对比分析，结果如表9。

检验结果表明，在正态分布的95%和99%置信水平下，创业板的实际失败天数均高于期望失败天数，实际失败频率均高于设定的显著性水平。这一方面证明我们对于创业板投资风险的技术估计过于乐观，VaR值，也就是最大可能性损失值被低估了;另外实际失败频率高于期望失败频率，也证明了创业板的实际投资风险，比技术估计的要高。

对比两个市场发现，创业板收益率的波动风险在正态分布下被严重低估，市场不稳定，风险较大。而在95%置信水平下，主板相对稳定，VaR方法能够相对较好的估测主板的波动风险。总的来说，无论是创业板还是主板，在正态分布假设下的风险都是被低估的。低估股市风险可能是由于我们的正态假定，忽略了分布的尾部特征。

当改变了收益率的分布假设后，实际的失败频率明显降低，创业板和主板在t-分布下均高估了风险，主板的风险被高估的更严重一些。说明虽然t分布能够较好的模拟股票收益率序列的波动聚集性，且t分布下序列的尖峰后尾性能够更好的体现出来，但是对于衡量在险价值VaR，t分布下的GARCH族模型估测的最大可能性风险值过于谨慎，不是最合理的选择。

4  结论

本文使用GARCH-VAR模型分别在正态分布、t分布和GED分布的假定下比较分析了创业板和主板的波动特征及市场风险，总体结果如下：

①创业板市场波动性比主板要大，我们通过建立GARCH-VaR模型来衡量创业板和主板的在险价值，发现创业板面临的风险大于主板。

②通过在险价值的失败频率检测，发现创业板的实际失败频率比主板要高，在正态分布和GED分布下，创业板的在险价值VaR被明显的低估了，创业板市场的实质风险要高于技术分析得出的市场风险。

③t分布和GED分布下的模型拟合结果最好，且在t分布和GED分布下估测出的VaR值相比正态分布下估测的VaR值值域更加宽泛，覆盖范围更广，说明t-分布和GED分布相比正态分布更能捕捉到股市收益率分布的尖峰厚尾特征。

④虽然建立在t分布和GED分布之上的GARCH族模型更能捕捉股票收益率波动的尖峰厚尾特征，体现波动的集聚性，但是在t分布下，创业板和主板的市场风险都被高估了，其中主板更加明显一些，说明t分布下的最大市场风险度量过于保守。

⑤GED分布假定下的主板在险价值度量效果较好，实际失败频率明显降低。说明考虑尖峰厚尾分布对于在险价值度量影响较大，t分布下的技术分析容易过于谨慎，从而高估风险，GED分布对在险价值的影响没有t分布下的大，在较高的风险水平下，预测相对准确。

综合上述分析，t分布和GED分布更能描述创业板和主板的波动特征，GED分布假定下的GARCH模型对于衡量波动特征和度量在险价值是最为恰当有效的。

参考文献：

[1]Markowitz H.. Portfolio Selection [J].The Journal of Finance，1952（2）： 77-91.

[2]Sharp W.. Capital Asset Prices： A Theory of Market Equilibrium under conditions of risk [J].The Journal of Finance，1964（3）： 425-442.

[3]Sharp W.. A Simplified Model for Portfolio Analysis[J]. Management Science， 1963（2）： 277-293.

[4]Arrow， K.. The Theory of Risk Aversion， the Theory of Risk-bearing[M]. Chicago： Markham， 1971： 90-120.

[5]Fama E.. The Behavior of Stock Market Prices[J]. Journal of Business， 1975，38（1）： 34-105.

[6]Cont R， Bouchaud J.. Head Behavior and Aggregate Fluctuations in Financial Markets [J]. Macroeconomic Dynamics，2000，4（2）： 170-196.

[7]吳文峰，吴冲锋.股票价格波动模型探讨[J].系统工程理论与实践，2000，20（4）：63-69.

[8]赵鹏举.反馈交易与证券市场收益的尖峰厚尾特征[J].系统工程，2009，27（2）：7-13.

[9]Bollerslev T，Engle R.F， and Wooldridge J. M. A Capital Asset Pricing Model with Time Varying Covariances [J]. Journal of Political Economy， 1988，96： 116-131.

[10]Bollerslev T，Engle R.F.. Common Persistence in Conditional Variances[J]. Econometrica，1993，61（1）： 167-186.

[11]Bollerslev T.. Generalized Autoregressive Conditional Heteroskedasticity [J]. Journal of Econometrics， 1986，31： 307-327.

[12]Bollerslev T.. A Conditional Heteroskedastic Time Series Model for Speculative Prices and Rates of Return [J]， Review of Economics and Statistics， 1987，69： 542-547.

[13]Glosten L. R， Jaganna T.. On the Relation Between the Expected Value and the Volatility of the Nominal Excess Return on Stocks[J].Journal of Finance，1993，8（5）： 1779-1801.

[14]Herwartz H.. Stock Return Prediction Under GARCH-An Empirical Assessment [J]. International Journal of Forecasting，2017（33）： 569-580.

[15]吴俊.上海银行间同业拆放市场杠杆效应——基于GARCH族模型的比较研究[J].管理现代化，2015，2015（1）：4-6.

[16]Huisman R， koedijk KG， Kool C J M. Tail-index estimates in small samples[J]. Journal of Business and Economic Statistics， 2001， 19： 2008-216.