向量形式的角平分线及其应用

李淼

【摘要】向量是近代数学中重要和基本的数学概念之一，是沟通代数和几何的一种工具.本文用向量形式表示了角平分线的充要条件及角平分线的性质，并给出了应用.

【关键词】向量;角平分线;性质

性质1点P在∠ABC的平分线上的充要条件是：

BP=kBA+BC|BA|+|BC|或写作BP·BA|BA|-BC|BC|=0.

事实上，由菱形的性质容易得到.

性质2三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.如图1所示，△ABC中，AD平分∠BAC，则ABAC=DBCD.

图1

证法一设AD的单位垂直向量为e，则

ABAC=AB·eCA·e=（AD+DB）·e（CD+DA）·e=DB·eCD·e=DBCD.

证法二设BDDC=λ，则AD=DCBD·AB+BDBC·AC=DCDC+BD·AB+BDBD+DC·AC=11+BDDCAB+BDDC1+BDDC·AC=11+λAB+λ1+λ·AC.

又AD在∠BAC的平分线上，

所以AD=kAB|AB|+AC|AC|.

根据平面向量基本定理可得：

11+λ=k|AB|，λ1+λ=k|AC|，

两式相除可得|AB||AC|=λ，所以DBCD=ABAC.

性质3若AD是△ABC中∠A的平分线，由角平分线的性质DBCD=ABAC，得

AD=AB+|AB||AC|·AC1+|AB||AC|=|AC|AB+|AB|AC|AB|+|AC|.

证明AD=DC·ABDC+BD+BD·ACBD+DC=DC·AB+BD·ACBD+DC=AB+BDDC·ACBDDC+1=AB+|AB||AC|·AC|AB||AC|+1=|AC|·AB+|AB|AC|AB|+|AC|.

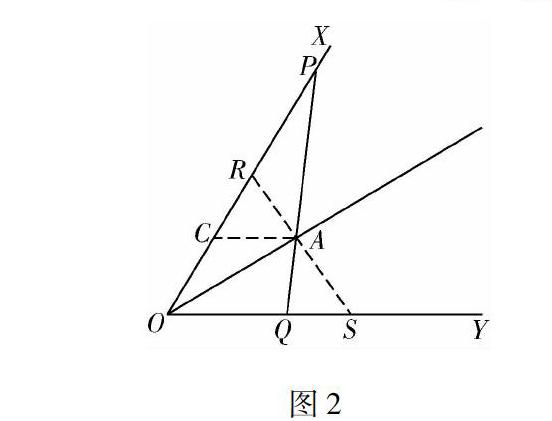
例1如图2所示，经过∠XOY的平分线上一点A，任作一直线与OX与OY分别交于P和Q，求证：1OP+1OQ为定值.

图2

证明过A作OA的垂线交OX和OY于R和S，则△ORS是等腰三角形，则：2OA=OR+OS=|OR||OP|·OP+|OS||OQ|·OQ，由于P，A，Q三点共线，因此|OR||OP|+|OS||OQ|=2，又因为|OR|=|OS|，所以1OP+1OQ=2OR.

例2在直角坐标系中，已知点A（0，1）和点B（-3，4），若点C在∠AOB的平分线上且|OC|=2，则OC=.

解析OC=λOA|OA|+OB|OB|

=λ（0，1）1+（-3，4）5=（0，λ）+-35λ，45λ

=-35λ，95λ，

|OC|2=925λ2+8125λ2=9025λ2=4，解得λ=103，

所以OC=-105，3105.

【參考文献】

[1]黄炳锋.一个向量结论在角平分线问题中的应用[J].福建中学数学，2008（5）：15-16.

[2]戴宏照，张培.向量几何意义的应用[J].中学生数学，2017（9）：9-10.

[3]谭亚英.角平分线的向量视角[J].数学学习与研究：教研版，2016（5）：140.

i-font-family：宋体'>