高速列车垂向随机振动及减振器阻尼参数优化

于曰伟， 周长城， 赵雷雷

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)

高速列车在运行过程中，轨道不平顺将直接经车轮传递到悬挂部件上，从而引起各部件的高频振动和低频振动，如果这种振动不经过合适的减振器衰减，则会降低机械部件的结构强度和使用寿命，甚至恶化列车的运行品质，这对运输的安全性、舒适性和经济性都是不利的[1]。为此，国内外学者针对高速列车减振器阻尼参数优化开展了诸多研究。然而，以往轨道车辆垂向悬挂系统模型中都采用弹簧和阻尼器并联的形式[2-4]，较少考虑减振器两端橡胶节点的弹性，但实际的轨道车辆垂向悬挂系统模型类似于推广的Ruzicka隔振模型，即减振器的两端都带有橡胶节点，其目的一方面是提高系统的隔振和降噪能力，另一方面是避免减振器两端相连部件其他方向的振动影响减振器的正常工作，以延长减振器的使用寿命[4-6]。

文献[7-8]首次通过建立高速客车垂向广义Ruzicka隔振模型，以车体位移均方值和车体加速度均方值为目标，对高速客车垂向悬挂参数进行了优化。然而，所建立的振动模型中未考虑轮对的振动位移，且优化目标函数中未考虑转向架构架的隔振效果，但实际在轨道不平顺激励下，轮对是运动的[9-10]，且减振器阻尼参数对转向架构架的振动响应是有影响的[1]。因此，本文进一步对高速列车垂向悬挂系统阻尼参数进行优化，并作为文献[7-8]的延伸和补充，分别建立不考虑和考虑轮对振动位移的高速列车垂向广义Ruzicka隔振模型，对其进行对比分析和验证；通过分析减振器阻尼参数对列车振动响应的影响，建立高速列车垂向减振器阻尼参数优化目标函数；在此基础上进行减振器阻尼参数优化，为高速列车垂向悬挂系统阻尼参数的选取提供理论依据。

1 高速列车垂向广义Ruzicka隔振模型

1.1 不考虑轮对振动位移

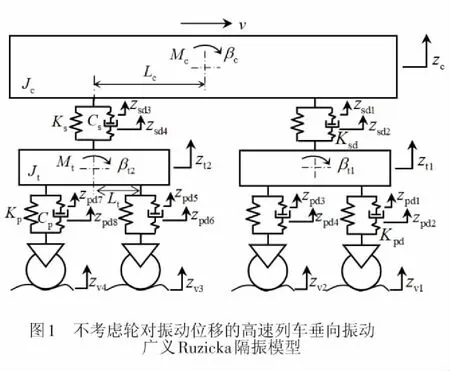
不考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型[7-8]，见图1。图中：Mc、Mt分别为车体质量之半和构架质量之半；Jc、Jt分别为车体和构架的点头转动惯量之半；Kp、Ks分别为一系和二系悬挂的一侧垂向刚度；Cp、Cs分别为一系和二系悬挂的一侧垂向阻尼；Kpd、Ksd分别为一系和二系垂向减振器的橡胶节点刚度；Lc、Lt分别为车辆定距之半和转向架轴距之半；zpd1～zpd8、zsd1～zsd4分别为一系和二系垂向减振器的两端垂向位移；v为车辆运行速度；zc、zt1、zt2分别为车体、前构架和后构架的垂向位移；βc、βt1、βt2分别为车体、前构架和后构架的点头角位移；zv1～zv4为轨道高低不平顺位移输入。

其中，zv2、zv3、zv4可用zv1表示为

( 1 )

式中：t为时间；τ为时间滞后，τ1=2Lt/v、τ2=2Lc/v、τ3=2(Lt+Lc)/v。

1.2 考虑轮对振动位移

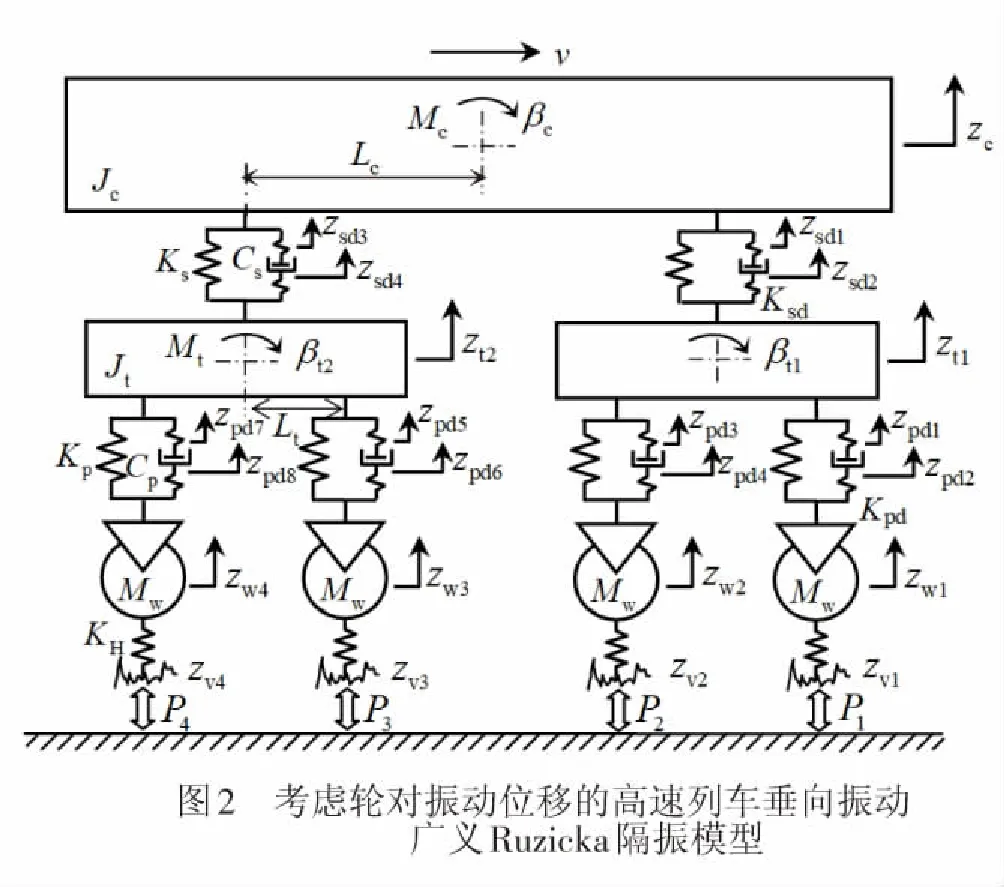
考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型[9-10]，见图2。图中，Mw为轮对质量之半；KH为轮轨等效线性接触刚度；zw1～zw4为轮对的垂向位移；P1～P4为轮轨作用力。

其中，轮轨等效线性接触刚度[10-11]

( 2 )

式中：P0为单侧轮轨静态作用力；G为轮轨接触常数，对于锥形踏面车轮G=4.57R-0.149×10-8m/N2/3，磨耗型踏面车轮G=3.86R-0.115×10-8m/N2/3，其中，R为车轮半径。

2 高速列车垂向振动微分方程

2.1 不考虑轮对振动位移

根据图1所示的不考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型和式( 1 )，由牛顿第二定律可导出系统的振动微分方程，即

( 3 )

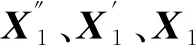
2.2 考虑轮对振动位移

根据图2所示的考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型和式( 1 )、式( 2 )，由牛顿第二定律可导出系统的振动微分方程，即

( 4 )

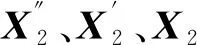
3 高速列车垂向随机振动响应特性

3.1 不考虑轮对振动位移

由振动微分方程式( 3 )可知，方程中含有6个加速度变量的二阶微分方程，同时含有12个速度变量的一阶微分方程，如不通过变换，无法将其表示为可求解形式的状态空间方程[12]。因此，为了方便求解，令Δzs1=zsd1-zsd2、Δzs2=zsd3-zsd4、Δzp1=zpd1-zpd2、Δzp2=zpd3-zpd4、Δzp3=zpd5-zpd6、Δzp4=zpd7-zpd8，可得如下变换关系

( 5 )

式中：i=1,2，j=3,4，m=5,6，n=7,8；仅当i=1，j=3，m=5，n=7时，式中的“±”取“+”。

将式( 5 )代入振动微分方程式( 3 )，可得

( 6 )

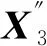
( 7 )

式中：系统矩阵

输入矩阵

输出矩阵C1=I18×18；传输矩阵D1=018×18；输入向量

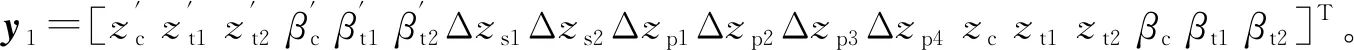
根据状态空间方程式( 7 )，利用Matlab编写计算程序并应用变步长四阶龙格-库塔法进行方程的求解，可得到不考虑轮对振动位移的高速列车垂向随机振动响应值。

3.2 考虑轮对振动位移

同理，根据上述方程变换方法，可将式( 4 )转化为以下形式

( 8 )

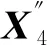
( 9 )

式中：系统矩阵

输入矩阵

输出矩阵C2=I26×26；传输矩阵D2=026×26；输入向量

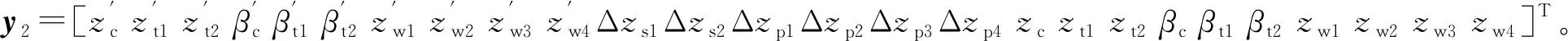
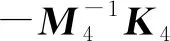
根据状态空间方程式( 9 )，利用Matlab编写计算程序并应用变步长四阶龙格-库塔法进行方程的求解，可得到考虑轮对振动位移的高速列车垂向随机振动响应值。

3.3 2种模型的随机振动响应对比

为比较2种模型之间的差别，以文献[13]提供的轨道车辆为应用实例，分析不考虑和考虑轮对振动位移的该轨道车辆垂向随机振动响应的不同，并将之与试验测试值相比较。该轨道车辆的模型参数为Mc=15 200 kg，Mt=600 kg，Mw=700 kg，Jc=1 019 000 kg·m2，Jt=700 kg·m2，Kp=875 000 N/m，Ks=412 000 N/m，Cp=34 000 N·s/m，Cs=108 500 N·s/m，Lc=3.289 m，Lt=0.797 m，R=0.28 m，车轮类型为磨耗型踏面车轮。

3.3.1 仿真分析

以目前应用较为广泛的德国轨道高低不平顺功率谱密度作为模型的输入激励，高低不平顺功率谱密度为[14]

(10)

式中：Ω为轨道不平顺的空间频率；Av为轨道粗糙度系数；Ωc、Ωr为截断空间频率；各已知参数见表1。其中，低干扰谱适合250 km/h及以上车速，高干扰谱适合250 km/h以下车速。

表1 高低不平顺参数

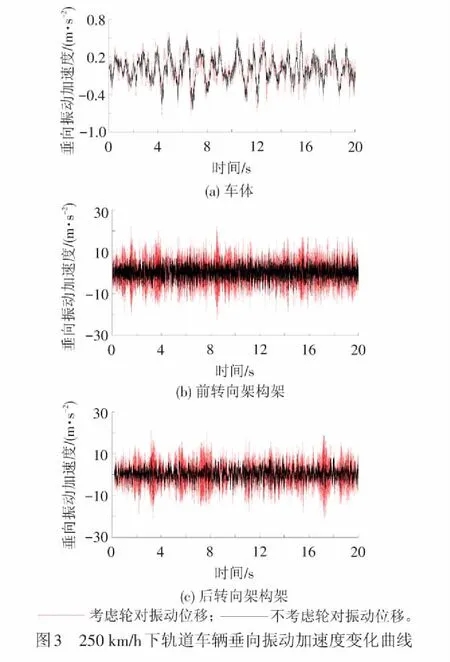
采用文献[15]的时频转换方法，将频域激励转换为时域样本，作为系统的输入，对不同模型下的该轨道车辆的垂向随机振动响应进行求解，得到的仿真对比结果见图3。其中，仿真时的一系垂向减振器和二系垂向减振器橡胶节点刚度的原始值均取为：5×107N/m；列车运行速度由200 km/h增加到300 km/h，速度增量步长为50 km/h，每个运行速度下的仿真时间长度为20 s；列车运行速度为200 km/h时采用德国高干扰谱，其余采用低干扰谱。由于在不同速度下的列车的垂向随机振动响应变化规律基本一致，且受篇幅关系影响，文中只列出了运行速度250 km/h下的仿真结果。

在不同运行速度、不同车辆模型下的该轨道车辆的垂向随机振动加速度的最大值见表2。

从图3和表2可以看出，2种模型下的车体垂向振动加速度值相差不大，两者几乎一致，而转向架构架垂向振动加速度值相差甚大，即考虑轮对振动与否，其结果主要影响构架的振动响应特征。

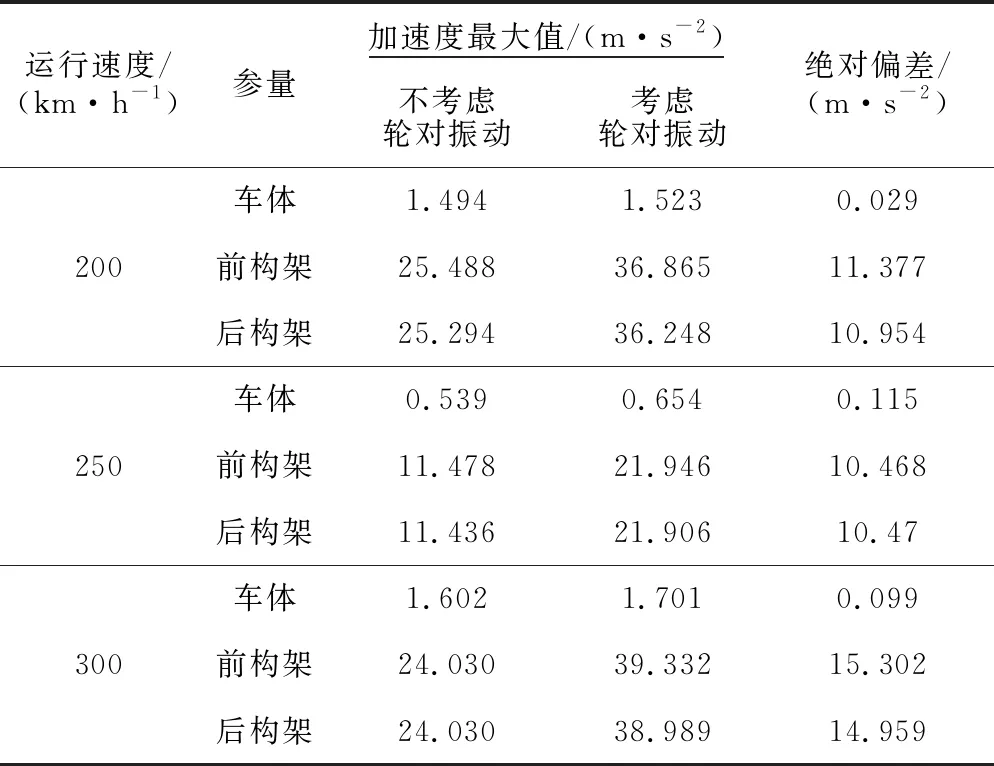
表2 仿真结果

3.3.2 振动响应试验对比

为验证2种模型的可靠性和正确性，利用文献[13]所提供的实车试验结果，将之与2种模型下的仿真结果进行对比分析。试验条件为：车辆以80 km/h的速度在60 kg/m钢轨、混凝土轨枕、普通碎石道床轨道上运行，仿真及试验结果对比见表3，其中仿真时采用德国高干扰谱。

由表3可知，考虑轮对振动位移的车辆模型的车体及构架垂向振动加速度的仿真结果与实车测试结果都比较吻合；不考虑轮对振动位移的车辆模型的车体垂向振动加速度与实车测试结果较吻合，而构架垂向振动加速度的仿真结果与实车测试结果相差较大。由此可见，考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型与实际情况更为相符，即在轨道不平顺激励下轮对是运动的，在进行高速列车垂向振动特性分析时应考虑轮对的振动。

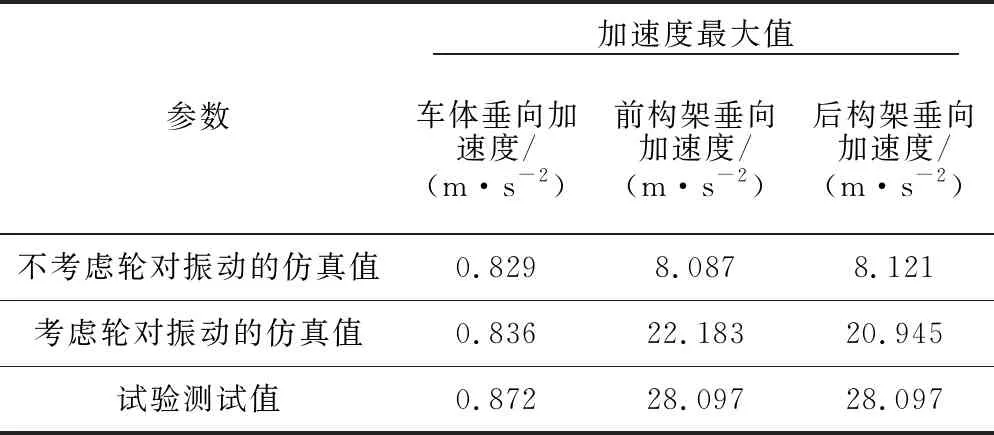
表3 仿真结果与试验结果对比

4 高速列车垂向减振器阻尼参数优化

一系垂向减振器和二系垂向减振器对高速列车的垂向运行平稳性有着决定性的影响，然而，两者在车辆中的主要作用有所不同，因此，要想获得理想的一系垂向减振器和二系垂向减振器阻尼参数设计值，首先必须明确2种减振器对高速列车垂向振动响应特性的影响，然后才能合理有效地对其阻尼参数进行设计。

4.1 减振器阻尼参数影响分析

为探明2种减振器阻尼参数对高速列车垂向振动响应特性的影响，以某250 km/h高速客车[11]为应用实例，将其原车辆参数作为分析的基准数值，利用考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型及其振动响应求解方法，对列车在250 km/h运行速度下的加速度振动响应均方根值及悬挂垂向行程均方根值进行计算。轨道输入激励模型见式(10)，车辆模型参数见表4；一系垂向减振器和二系垂向减振器的橡胶节点刚度值均为5×107N/m。

表4 某250 km/h高速客车参数

在分析某减振器阻尼参数对振动响应量的影响时，将其基准数值增大100%或减小50%，其余参数保持不变，此外，参数值及响应均方根值以基准数值为基准作无量纲化处理(即将各参数值和响应均方根值作如下处理：Cp/Cpb，Cs/Csb，σr/σrb，b代表基准，即Cpb、Csb分别为原列车一系垂向、二系垂向减振器阻尼参数，r代表响应)，分析时参数取值见表5。

表5 系统参数取值

4.1.1 一系垂向减振器的影响分析

一系垂向减振器阻尼参数为15 000、30 000、60 000 (N·s)/m，而其他参数保持不变时，所得到的车体和构架垂向振动加速度及悬挂垂向行程随一系垂向减振器阻尼参数变化的曲线见图4。

由图4可见，一系垂向减振器对列车构架垂向振动加速度和一系悬挂垂向行程影响较大，而对车体垂向振动加速度和二系悬挂垂向行程影响较小。

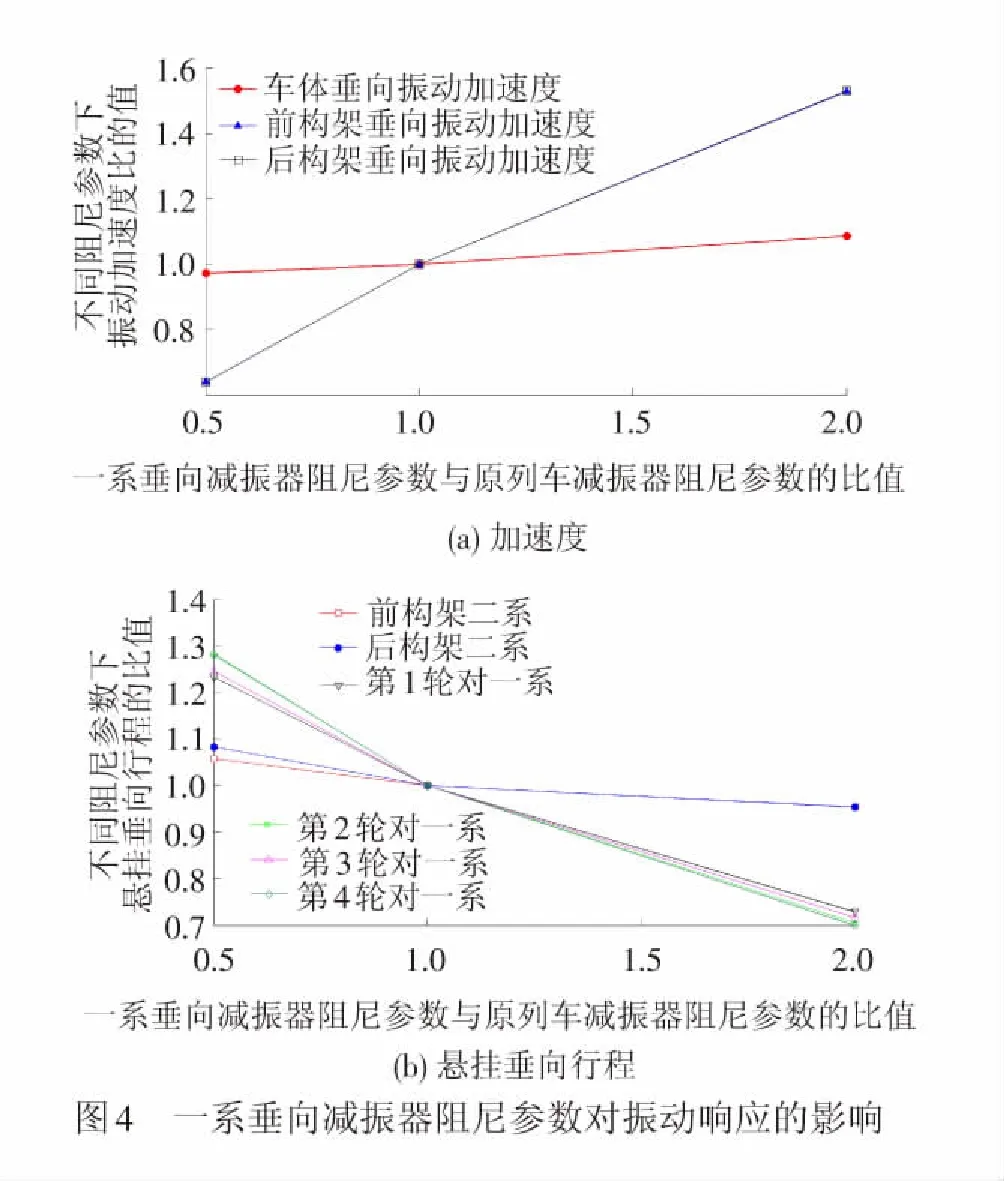
4.1.2 二系垂向减振器的影响分析

二系垂向减振器阻尼参数为20 000、40 000、80 000 (N·s)/m，而其他参数保持不变时，所得到的车体和构架垂向振动加速度响应及悬挂垂向行程响应随二系垂向减振器阻尼参数变化的曲线见图5。

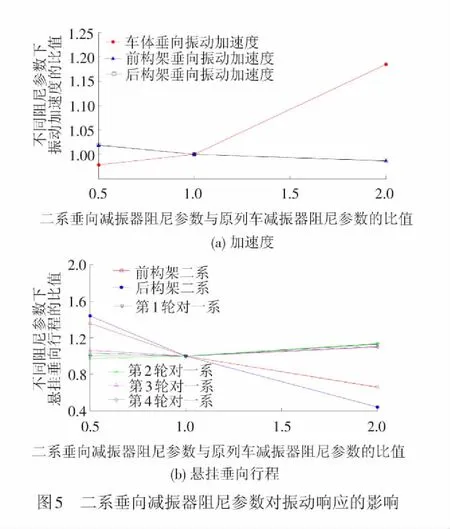
从图5可以看出，二系垂向减振器主要影响列车车体垂向振动加速度和二系悬挂垂向行程，对构架垂向振动加速度和一系悬挂垂向行程影响较小。

综上分析可知，一系垂向减振器主要用于衰减轴箱与转向架构架之间的垂向振动，二系垂向减振器主要用于衰减车体与转向架构架之间的垂向振动。因此，若要单独对一系垂向减振器的阻尼参数进行优化，需侧重考虑构架的隔振效果；若要单独对二系垂向减振器的阻尼参数进行优化，需侧重考虑车体的隔振效果；若要同时对这2种减振器进行优化，则需兼顾构架和车体两者的隔振效果。

4.2 减振器阻尼参数多目标优化

4.2.1 优化设计目标函数

对于轨道车辆随机振动，悬挂垂向行程均方根值和加速度均方根值是评价系统隔振效果的两项重要指标[7-8]。由图4、图5可以看出，前构架和后构架的垂向振动加速度均方根值及二系悬挂垂向行程均方根值大小基本一致，且各一系悬挂垂向行程均方根值大小也基本一致，此外，本文目的在于对高速列车一系和二系垂向减振器阻尼参数进行优化，因此为简化优化目标，以前构架垂向振动加速度均方根值、前构架二系悬挂垂向行程均方根值、第1轮对一系悬挂垂向行程均方根值、车体垂向振动加速度均方根值作为目标，确定系统优化目标为

(11)

式中：σz″c为车体垂向振动加速度均方根值；σfc为前构架二系悬挂垂向行程均方根值；σz″t1为前构架垂向振动加速度均方根值；σft1为第1轮对一系悬挂垂向行程均方根值；x为设计变量，x=(Cp,Cs)；fc为前构架二系悬挂垂向行程，fc=zc-βcLc-zt1；ft为第1轮对一系悬挂垂向行程，ft=zt1-βt1Lt-zw1。

由式(11)可以看出，高速列车一系和二系垂向减振器阻尼参数优化是一个多目标、多参数同时优化问题。本文采用线性加权和法构造评价函数，从而将该多目标函数转化为单目标函数进行求解。其中，在对各子目标函数进行线性加权求和时，采用无量纲归一化处理，所得到的新目标函数，即评价函数为

(12)

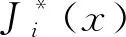
4.2.2 加权因子选取及优化参数取值范围

基于前述分析，以悬挂垂向行程均方根值和加速度均方根值为参照，分别考虑在不同优化条件下的列车车体垂向振动响应，构架垂向振动响应，一系悬挂垂向振动响应和二系悬挂垂向振动响应情况，并将不同优化条件下的各子目标的重要程度视为等同，确定如下各加权因子值，见表6。

表6 加权因子取值

表6中，第一组为评价函数中只考虑车体垂向振动加速度均方根值和构架垂向振动加速度均方根值；第二组为评价函数中只考虑一系悬挂垂向行程均方根值和二系悬挂垂向行程均方根值；第三组为评价函数中考虑车体垂向振动加速度均方根值，构架垂向振动加速度均方根值，一系悬挂垂向行程均方根值和二系悬挂垂向行程均方根值。

为了能够得到较为可靠地高速列车垂向悬挂系统参数优化设计结果，根据设计要求，将各减振器阻尼参数以原列车参数为中心，上下浮动50%作为优化参数的上下极限，确定优化参数取值范围，见表7。

表7 优化参数取值范围

4.2.3 优化设计方法

多岛遗传算法作为一种伪并行遗传算法，可有效避免早熟和加快收敛速度，可以很好地在优化域中寻找全局最优解。本文采用多岛遗传算法[16]，利用考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型及其振动响应求解方法，对高速列车一系垂向减振器和二系垂向减振器的阻尼参数进行优化，优化流程见图6，其中，多岛遗传算法的子群规模为10，岛个数为10，进化代数为10，交叉概率为1，变异概率为0.01，迁移概率为0.01，迁移的间隔代数为5。

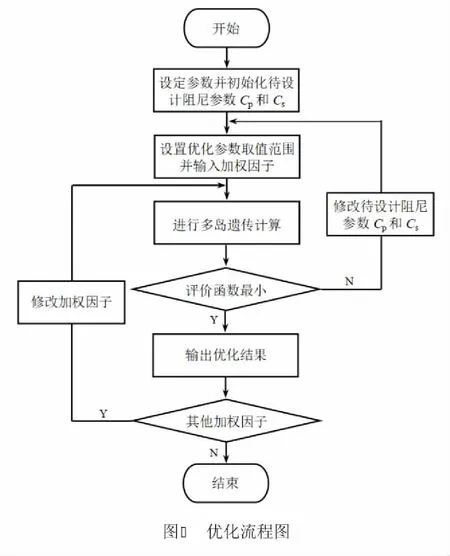
根据列车参数，以德国轨道高低不平顺(见式10)作为系统的输入激励，依据图6所示的优化流程，利用所编写的优化程序求评价函数Jm的最小值，便可得到一系垂向减振器和二系垂向减振器阻尼参数的优化设计值，即Cp、Cs。

4.2.4 优化实例及结果分析

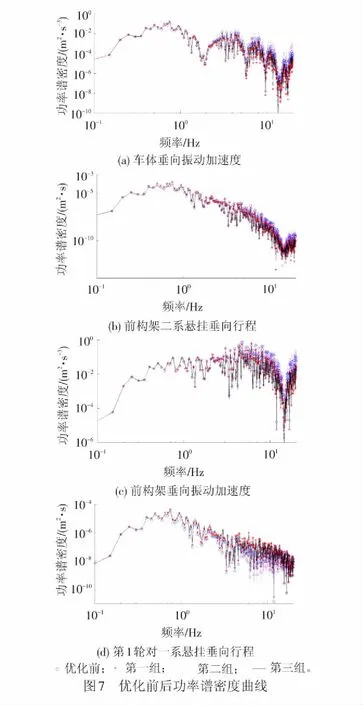
以某250 km/h高速客车为例，对其一系垂向减振器和二系垂向减振器的阻尼参数进行优化，车辆模型参数见表4。优化时的列车运行速度取为250 km/h，时间长度设置为60 s，优化结果见表8，所得到的优化前的振动响应与优化后的不同加权因子下的振动响应的功率谱密度对比曲线见图7。

表8 阻尼参数优化结果

从图7可以看出：第一组加权因子下(即以车体垂向振动加速度均方根值和构架垂向振动加速度均方根值作为评价函数)：车体和构架垂向振动加速度功率谱密度较之优化前有所降低，但一系悬挂和二系悬挂垂向行程均有所增大；第二组加权因子下(即以一系悬挂垂向行程均方根值和二系悬挂垂向行程均方根值作为评价函数)：优化后一系悬挂和二系悬挂垂向行程的功率谱密度明显优于优化前，特别是在低频部分明显降低，但二系悬挂垂向行程在高频部分有所增大，且车体和构架垂向振动加速度功率谱密度显著增大；第三组加权因子下(即以车体垂向振动加速度均方根值，构架垂向振动加速度均方根值，一系悬挂垂向行程均方根值和二系悬挂垂向行程均方根值作为评价函数)：车体和构架垂向振动加速度功率谱密度及二系悬挂垂向行程功率谱密度，较之优化前有所降低，但一系悬挂垂向行程有所增大，特别是在高频部分更为明显，总体而言，优化后车体和构架的随机隔振能力有所增强。

根据表8优化结果及以上分析，可得到高速列车随机振动减振器阻尼参数取值的一般规律：在参数取值区间内，一系垂向减振器阻尼取较小值，二系垂向减振器阻尼在30～50 (N·s)/m间取值，有利于高速列车的随机隔振。

4.2.5 优化效果对比分析

以往对于轨道车辆垂向减振器阻尼参数的优化，通常忽略减振器阻尼参数对转向架构架隔振效果的影响，仅考虑其对车体隔振效果的影响，然而实际上高速列车系统各参数是相互影响且共同对客车的动态性能起作用的，即减振器阻尼参数对车体振动响应和转向架构架振动响应两者皆具有一定的影响，为了进一步分析本文所建立减振器阻尼参数优化方法的优化效果，将其与传统优化方法进行对比分析。其中，传统优化方法[7-8]的评价函数中只考虑车体垂向振动加速度均方根值和二系悬挂垂向行程均方根值，即将式(12)中的加权因子ω3、ω4取为零，加权因子值见表9。

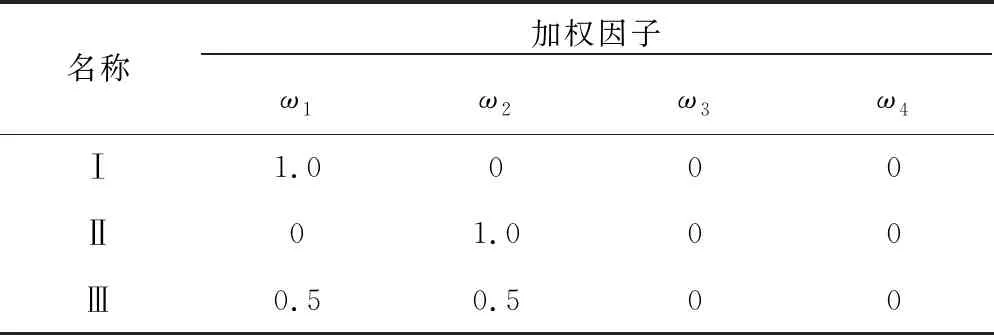
表9 传统优化方法下的加权因子值

注:Ⅰ为评价函数中只考虑车体垂向振动加速度均方根值；Ⅱ为评价函数中只考虑二系悬挂垂向行程均方根值；Ⅲ为评价函数中考虑车体垂向振动加速度均方根值和二系悬挂垂向行程均方根值。

利用考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型及其振动响应求解方法，对传统优化方法加权因子(见表9)下的减振器阻尼参数进行优化，并计算各优化参数下所对应的系统振动响应均方根值，以优化前的系统振动响应均方根值为参照，得到各加权因子下的系统振动响应均方根值的相对值变化曲线，见图8。

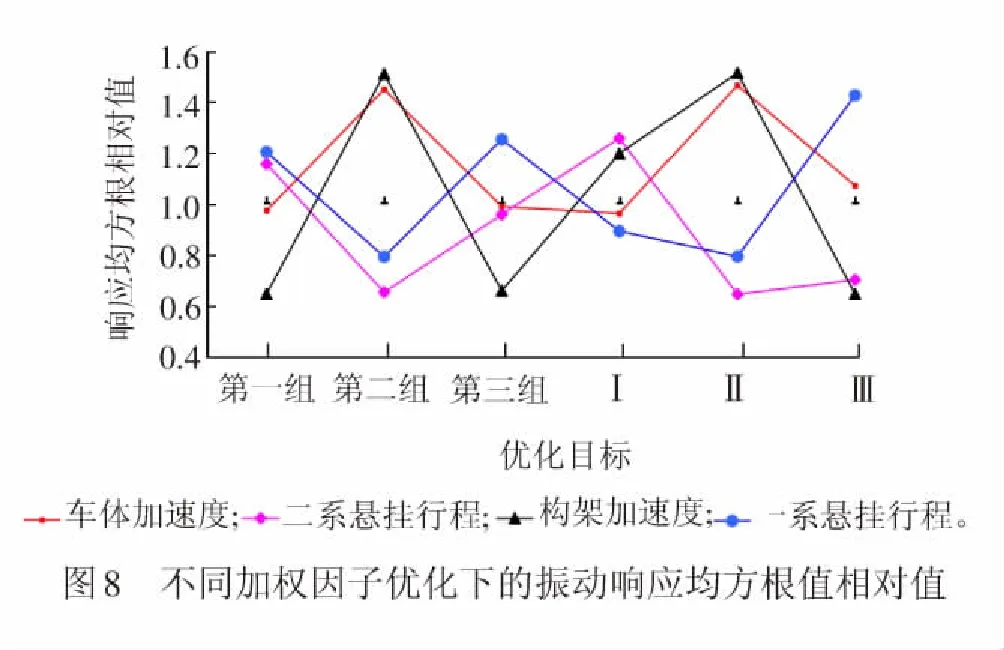
由图8可见，由第一组和Ⅰ组对比可知：优化时若仅以车体垂向振动加速度均方根值为优化目标，构架的隔振效果变差；由第二组和Ⅱ组对比可知：优化时以二系悬挂垂向行程均方根值和一系悬挂垂向行程均方根值为优化目标或仅以二系悬挂垂向行程均方根值为优化目标，所得车体隔振效果和构架隔振效果相差不大；由第三组和Ⅲ组对比可知：以车体垂向振动加速度均方根值，构架垂向振动加速度均方根值，二系悬挂垂向行程均方根值和一系悬挂垂向行程均方根值为优化目标对减振器阻尼参数进行优化，列车整体隔振效果优于仅以车体垂向振动加速度均方根值和二系悬挂垂向行程均方根值为优化目标对阻尼参数进行优化。

通过以上分析可知，本文所建立的高速列车垂向减振器阻尼参数优化方法能够兼顾车体和构架的隔振效果，即该方法与传统方法相比，能够进一步改善列车的运行品质。

5 结束语

基于不考虑和考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型，通过方程变换，得到了便于数值积分求解的高速列车垂向振动状态空间表达式，在此基础上，对2种振动模型进行了比较。仿真与实车试验结果表明，考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型与实际情况更为吻合。基于考虑轮对振动位移的高速列车垂向振动广义Ruzicka隔振模型，分析了减振器阻尼参数对列车振动响应的影响，并以车体垂向振动加速度，二系悬挂垂向行程，构架垂向振动加速度，一系悬挂垂向行程均方根值为目标，应用评价函数法对减振器阻尼参数进行了优化，分析比较优化后的结果可知，该优化方法可进一步改善列车的运行品质。该研究为高速列车垂向减振器阻尼参数的选取提供了参考依据。