基于时空状态网络的高速铁路乘务交路计划优化研究

张哲铭， 王 莹， 廖正文,3， 曹文慧

(1. 杭州派迩信息技术有限公司， 浙江 杭州 311100； 2. 北京交通大学 交通运输学院， 北京 100044；3. 北京交通大学 轨道交通控制与安全国家重点实验室， 北京 100044； 4. 北京国邮科迅科技发展有限公司， 北京 100032)

乘务计划问题(CPP)是高速铁路调度领域的经典问题，计划结果直接影响高速铁路的运营效率和成本。乘务交路计划问题(CSP)作为CPP中的核心问题一直备受国内外学者关注。CSP是VRP类问题，其难点在于需要动态考虑乘务组休息和用餐时间，使该问题不能如同VRP一样利用基于时空网络(Time Space Network，TSN)的网络流模型刻画，故多数既有研究将其转化为基于可行乘务交路的集合覆盖问题，并借助列生成技术[1-6]或启发式算法[7-10]求解。

在网络和模型构造方面，TSN按构造方式主要分为两类：时空接续网(Time Space Connection Network，TSCN)和时空轴线网(Time Space Time Line Network，TSTLN)[11]。在铁路运输组织领域，TSCN由表示具体运行任务的点和表示任务间可行接续关系的弧组成，适用于刻画带有相对时间——“时长”约束的问题，见图1。TSTLN由表示运行任务时空节点的点和表示相邻时空节点间连续关系的弧组成，适用于刻画带有绝对时间——“时刻”约束的问题，见图2。在高速铁路CSP的乘务规则中，既有“时长”约束(如乘务组单次驾驶时长等)，又有“时刻”约束(如用餐时间窗)。因此CSP是同时包含“时长”和“时刻”约束的混合时间问题。但是，既有研究大多选择TSCN描述该问题，详细刻画“时长”约束，而很少考虑“时刻”约束。以用餐约束为例，在规定的时间段吃一日三餐是大多数中国人的习惯，既有研究通常假设乘务组休息时用餐，且不固定休息时间段，这导致了乘务组用餐时间不规律。只有文献[12]考虑了固定时间窗用餐约束，但其只针对公交领域，与高铁领域还有所差别。在求解算法方面，采用列生成技术求解带有资源约束最短路的价格子问题时，每次搜索最短路时都要考虑乘务规则，设计多标签最短路算法，效率不高。启发式算法尽管求解速度快，但却无法保证求解质量。

对此，本文以高速铁路CSP作为混合时间问题的代表，在构建网络模型时一次性考虑乘务规则约束，生成可以涵盖所有可行乘务交路的网络，针对网络规模过大导致求解效率与质量无法保证的问题，将乘务规则转化为可以控制网络规模的网络生成策略，并借助拉格朗日松弛技术求解。首先，基于二维TSTLN构建三维时空状态网络(Time Space State Network，TSSN)刻画CSP。即在TSTLN上引入状态维度，每个点新引入的状态坐标代表乘务组访问该点时的乘务状态，相邻节点间状态坐标的变化表示一个符合乘务规则的任务弧，而由若干个任务弧组成的，从起点到终点的一条时空路径就是一个乘务交路。其次，基于乘务规则，提出时空节点状态坐标递推原则和乘务任务可行转化判定条件，将乘务规则解析为网络生成策略融入TSSN，控制网络规模，同时简化数学模型。然后，基于TSSN建立0-1整数规划模型，通过拉格朗日松弛算法松弛“难约束”，从而将原CSP分解为多个独立乘务交路的时空最短路径子问题集合，摘除子问题间的耦合性，同时保证求解质量和效率。最后，通过实例对本文方法进行验算。

1 问题描述

CSP是根据乘务规则确定各乘务组从乘务基地出乘至返回该基地退乘过程中执行乘务任务的顺序。乘务任务包括：(外段)出乘任务、接续任务、运行任务、用餐任务、换乘任务、间休任务、外段驻班任务、(外段)退乘任务。高速铁路乘务交路的时间长度通常为1 d，但也存在2～3 d长交路的情况，此时需要安排乘务组外段驻班，每天的作业内容称为乘务交路段。具体的乘务规则如下[2]：

(1) 交路段规则μ为乘务组每天从出乘至退乘的上班时长，min；Tμ、Tμ分别为乘务交路段最小、最大时长，min。必须满足μ∈[Tμ,Tμ]。

(2) 换乘规则 乘务组连续担当不同动车交路的乘务区段时，ε为其间隔时间，min；Tε、Tε分别为最小、最大乘务换乘时间，min。必须满足ε∈[Tε,Tε]。

(3) 间休规则 乘务组连续担当乘务区段一段时间后必须进行间休，τ为间休时间，min；Tτ、Tτ分别为最小、最大间休时间，min。必须满足τ∈[Tτ,Tτ]。

(4) 连续驾驶规则λ为乘务组连续担当乘务区段的线上工作时间(含换乘时间)，min；Tλ、Tλ分别为最小、最大连续乘务时间，min。必须满足λ∈[Tλ,Tλ]，且连续驾驶后必须进行间休后方可值乘下一驾驶任务。

(5) 外段驻班规则 乘务组外段退乘休息时，η为其休息时间，min；Tη、Tη分别为最小、最大非基地乘务休息时间，min。必须满足η∈[Tη,Tη]。

(6) 用餐规则 乘务组必须在中午或晚间规定的用餐时间窗Wlun、Wdin内用餐。e为用餐时长，min；Te、Te分别为最小、最大用餐时长，min。必须满足e∈[Te,Te]。

(7) 乘务交路规则 乘务组的出乘和退乘站点必须是同一乘务基地，最大持续天数不超过Tv。

2 TSSN

2.1 状态维度的定义

TSTLN中，包含表示时刻的时间属性t和表示地点的空间属性s。而在TSSN中，除时间属性t和空间属性s，还需状态属性ω，即(t,s,ω)。如第i个时空节点的第m个状态定义为

TSTLN和TSSN的对比见图3。图3中A、B、C分别表示站点，A站为乘务基地所在站，点0和点9分别代表乘务基地虚拟起、终点，其余点均为乘务区段时空节点。

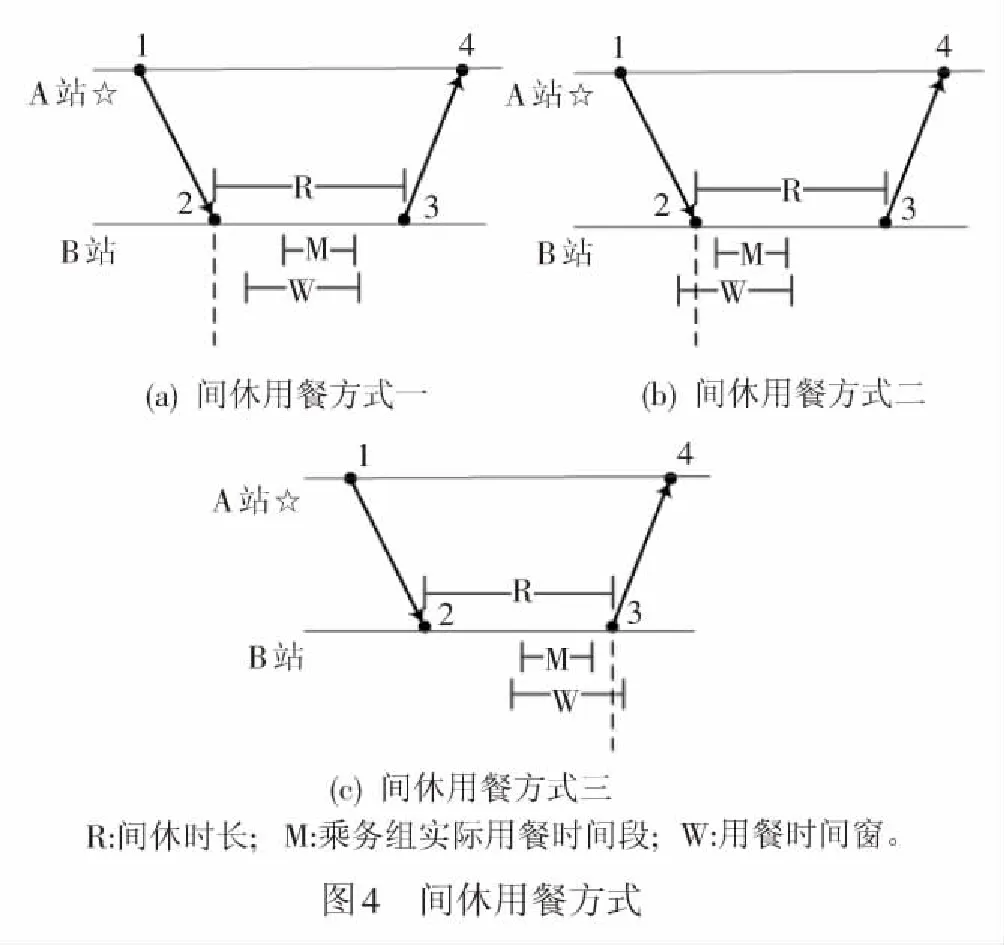
本文定义了两种用餐方式：

(1) 间休用餐 乘务组的用餐时间窗与间休时间窗交集，且交集部分不小于Te，此时默认组员在间休时用餐。

具体情况见图4、图5。

2.2 网络生成策略

在TSSN，时空节点状态坐标递推原则和乘务任务可行转化判定条件为点和弧生成策略。

点生成策略：除虚拟起点外所有节点的状态坐标，均由该点的前继节点的状态坐标和入弧所代表的乘务任务递推得出。

弧生成策略：除出乘弧外所有节点的出弧任务，均由该点的入弧代表的乘务任务和状态坐标递推得出。

因此，在所有乘务基地的虚拟起点和出乘弧已知的条件下，不断交替使用点和弧生成策略即可构建TSSN。

2.2.1 时空节点状态坐标递推原则

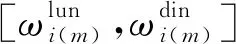
2.2.2 乘务任务可行转化判定条件

在TSSN中，所有类型的乘务任务均可通过不同类型的弧表示，除虚拟起点外的所有节点的出弧所代表的乘务任务均由该点的状态坐标和入弧任务决定。乘务任务可行转化关系见图7。

表1 乘务任务可行转化判定条件

2.3 网络生成示例

为了详细说明TSSN的生成策略，本文分别列举在无用餐规则和有用餐规则条件下的TSSN生成过程。

以图3(a)为例，uij为线段所代表乘务任务。假设：(1)各区间运行时间均为30 min；(2)列车在B站的接续时间为10 min；(3)列车在C站的折返时间为20 min；(4)A站为乘务基地所在站，乘务组的出乘时间tg、退乘时间tb为tg=tb=60 min；(5)点1所在时刻为11:00。

2.3.1 无用餐规则

假设：(1)最小换乘时间为10 min；(2)不规定固定的用餐时间窗；(3)连续值乘3 h左右退乘；(4)乘务规则参数：[Tλ,Tλ]=[150,180]min、[Tτ,Tτ]=[+∞,+∞]、[Tε,Tε]=[10,100]min、 [Tμ,Tμ]=[270,300]min。

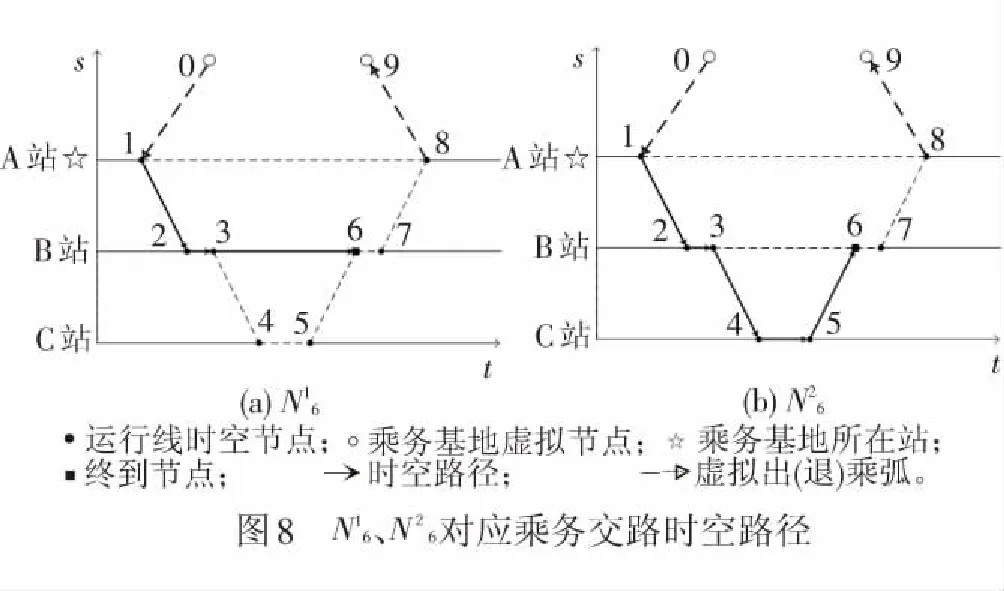
2.3.2 有用餐规则

2.4 构建TSSN

2.4.1 建立TSTLN

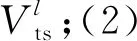
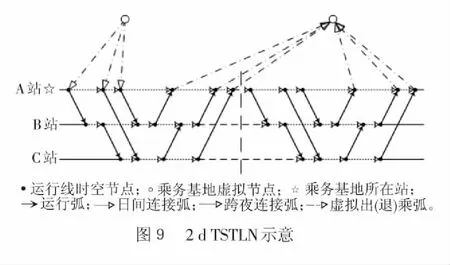
2.4.2 状态维度的引入

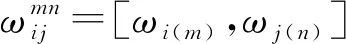
在广度优先遍历(Breadth First Search，BFS)过程中，TSTLN中的每个时空节点的不同状态均会被转化为TSSN中的一个时空状态节点，相邻时空节点间不同的状态转换均会被转化为TSSN中的一条时空状态转换弧，从而构成TSSN，记为Gtss=(Vtss,Atss)，Gtss表示TSSN，Vtss和Atss分别表示TSSN中的点集合和弧集合。简而言之，在TSTLN中引入状态维度后的变化为：(1)时空节点i的m个状态ωi=[ωi(1),ωi(2),…,ωi(m)]变为TSSN中m个时空状态节点；(2)连接各个时空状态节点的弧表示不同的乘务任务。

Step1统计乘务基地个数Ncb，并将乘务基地排序，令循环变量k=1。

Step3若k=Ncb，算法停止；否则，k=k+1，转入Step2。

3 基于拉格朗日松弛的优化模型及求解方法

3.1 初始模型

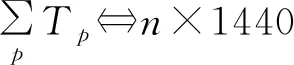
( 1 )

( 2 )

( 3 )

( 4 )

( 5 )

式( 1 )表示乘务任务总累计时间最小的总目标；式( 2 )表示所有乘务区段必须被覆盖约束，且该乘务区段允许“便乘”；式( 3 )表示流平衡约束，式( 4 )表示每个乘务交路的初始任务必须为出乘任务约束；式( 5 )表示决策变量取值范围约束。

3.2 优化模型

在TSSN中，若乘务交路p∈P出现在最优解中，则意味着p包含具体由乘务任务弧；否则，p选中虚拟停驻弧，代表执行p的乘务组处于休息状态。本文采用拉格朗日松弛算法求解，其本质是利用拉格朗日乘子对“难约束”所对应的资源“定价”，将“难约束”松弛到目标函数中，原问题随即被分解为由多个“简单约束”构成的子问题，简化模型求解，同时又为原问题提供了一个可靠下界，然后不断迭代求解子问题，在此过程中持续通过次梯度算法持续更新拉格朗日乘子，这也就相当于对“难约束”所对应的资源“动态定价”，从而不断提升下界，直至收敛。在CSP中，需要被“动态定价”的资源有两类，一类是式( 2 )对应的乘务区段资源l，其决定了乘务组值乘的乘务内容；另一类是停驻资源，其保证了乘务组大休。此外，由于CSP是“匿名”计划，所有p之间无差别，这种对称性会导致收敛效果不佳。对此，本文在不破坏3.1节中模型结构的前提下，通过两个方法解决上述问题：(1)添加式(10)对停驻资源“动态定价”；(2)为∀p∈P赋予权重gp规定p之间的顺序。

( 6 )

( 7 )

( 8 )

( 9 )

(10)

(11)

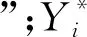
与初始模型相比，该模型改变了目标函数，增加权重gp、迭代次数k和式(10)。式( 6 )中gp为乘务区段l对于p的“会员折扣”，p在选择l时所付“实际费用”等于l的“市场价格”(弧长)与“会员折扣”的乘积。虽然gp会改变初始模型的总目标，但不会改变完成CSP所用的实际乘务组数，所以引入gp并不破坏模型结构。式(10)表示第k次迭代时，乘务基地i的虚拟停驻弧被覆盖的次数不小于前k-1次迭代的最优值，该约束不仅能对停驻资源“定价”，还能通过当前最优上界给拉格朗日对偶问题反馈，加速收敛。

3.3 拉格朗日对偶问题

在优化模型中，式( 7 )和式(10)使p间相互制约而耦合，为该模型的“难约束”，影响求解速度。因此，通过拉格朗日乘子惩罚项的形式将其松弛到目标函数中，余下所有约束均作用于单个p，原CSP被分解为针对每个p的时空最短路径问题集合，从而解除各个p间的耦合性，提高求解效率。拉格朗日松弛对偶问题优化模型为

L(ρ,δ)=

(12)

(13)

(14)

(15)

式中：ρ(k)(l)、δ(k)(i)分别为第k次迭代乘务区段资源和停驻资源的拉格朗日乘子，代表解不满足式( 7 )和式(10)时的惩罚值。

式(12)经等价变换后可得

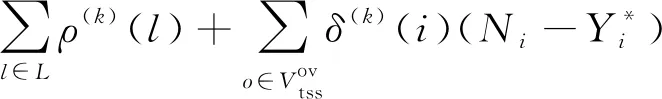
(16)

对于每个p的时空最短路径问题，本文选择前向动态规划算法(Forward Dynamic Programming，FDP)[13]求解。

3.4 拉格朗日乘子的更新方法

L(ρ,δ)的目标值随着ρ和δ的变化而改变。因此，在迭代过程中，需要不断更新ρ和δ。次梯度更新方法如下：

ρk+1(l)=

(17)

δk+1(i)=

(18)

式(17)、式(18)中，求和公式分别表示各资源被覆盖的次数，迭代过程中相应资源被选中的次数一旦变化，ρ和δ的值也会随之改变，而每一次变化都相当于在下一次迭代中对各资源重新“定价”，“动态定价”的特性就体现于此。每一次“动态定价”后，各个乘务交路会选择由各资源组成的“最便宜”的时空路径以满足需求。

推而广之，不仅仅是CSP， 诸如VRP类的带有“混合时间”约束的活动资源优化问题均可以采用此种求解策略。通过对固定资源(CSP中是乘务区段)的“动态定价”和活动资源(CSP中是乘务交路)为满足自身需求对固定资源的“市场选择”这两个过程的不断迭代[14]，从而解决活动资源优化的本质问题——活动资源和固定资源的最佳时空映射关系问题[6]。

3.5 拉格朗日松弛启发式算法

在求解L(ρ,δ)时，所得下界解不一定是原问题的可行解。当下届解不可行时，需要设计拉格朗日松弛启发式算法求得可行上界解。本文设计的拉格朗日松弛启发式算法是根据下界解中各乘务区段被覆盖情况作为启发信息。在迭代过程中，被下界解选中的乘务区段被视为有利于乘务组值乘的区段，故在启发式算法中应该优先被乘务交路选择。若上界解中存在多次被选中的乘务区段，则意味着乘务组“便乘”在此区段发生。在实际问题中，乘务组“便乘”会增加运营成本，所以在求解时应尽可能避免。所有乘务区段均被执行后，应安排剩余的乘务交路选择虚拟停驻弧，避免乘务资源浪费。具体算法如下：

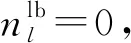
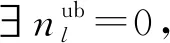
Step5若p=Np，算法结束；否则，令p=p+1，转入Step3。

综上所述，拉格朗日松弛算法框架见图10。

4 实例验证

本文分别利用发车密度大的城际铁路和高速铁路网CSP实例(以郑州东站乘务基地为中心，京广线北京西至武汉段、郑西线、郑徐线和郑州城际线组成的路网，以下简称“郑州东路网”)对该本文方法进行验算。在城际铁路CSP实例中，因其发车密度大、换乘机会多适宜采用本文设计的固定时间窗用餐规则进行乘务任务安排，而在发车密度小、换乘机会少的郑州东路网CSP实例采用何时休息何时用餐的规则。TSSN和拉格朗日松弛算法均利用C#语言在运行环境为Intel(R) Core (TM)i7-7500U 2.70 GHz，8.00 GB内存的个人计算机上编程实现。

京津城际铁路的交路时间长度较短，假设：(1)单司机值乘；(2)到站立即折返，最小折返时间15 min；(3)允许换乘；(4)不允许外段驻班；(5)设置用餐时间窗；(6)线上值乘4 h左右后直接退乘；(7)出、退乘时间各1 h。

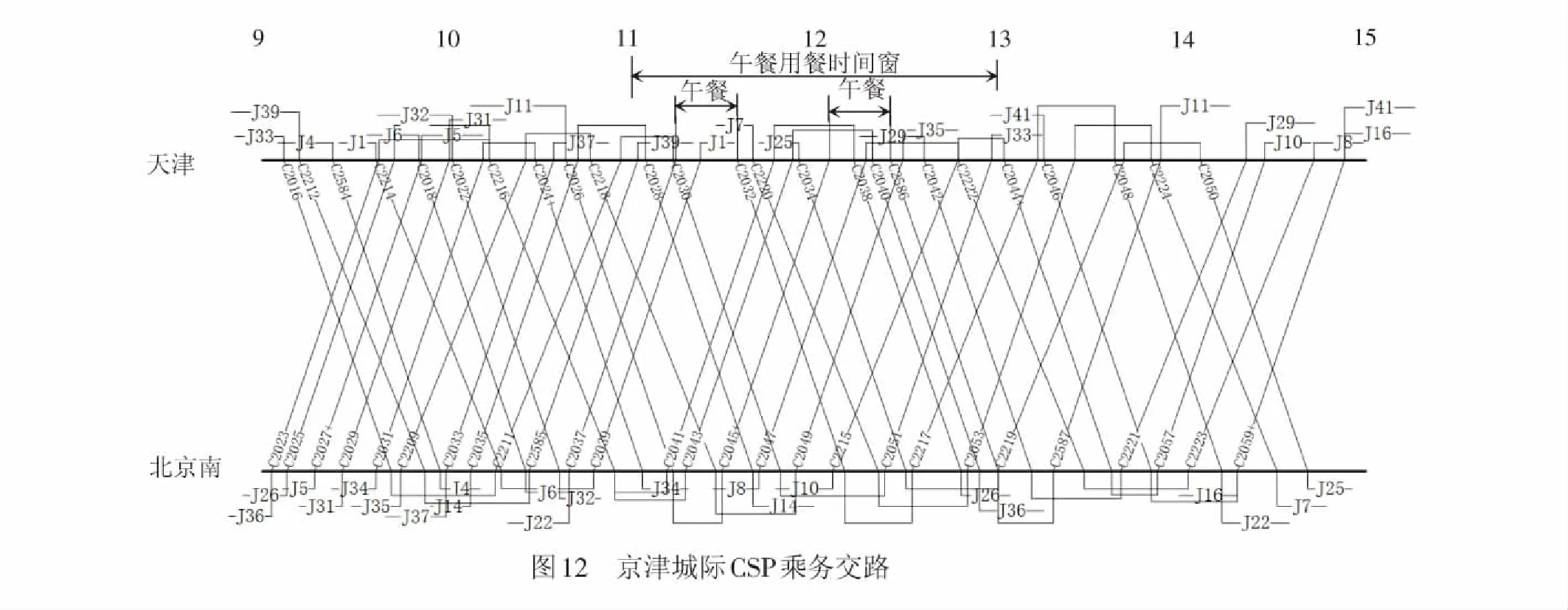
据此，以京津城际158个乘务区段为输入，各乘务规则参数如下：Np=60(北京南站和天津站各30条)，[Tμ,Tμ]= [300,370], [Tε,Tε]= [15,40]，[Tτ,Tτ]=[+∞,+∞]，[Tη,Tη]=[+∞,+∞]， [Tλ,Tλ]= [180,250]，[Te,Te]= [20,40]，Wlun= [11:00,13:00]，Wdin= [17:00,19:00]。迭代1 000次，共求得47条乘务交路，北京南站23条，需23组乘务组，天津站24条，需24组乘务组，用餐5次，最优上界为98 726.00，最优下界为81 466.68，对偶间隙为17.48%，求解时间为27 001.27 s。计算结果见表2，迭代曲线和部分乘务交路见图11、图12。

表2 京津城际CSP计算结果

郑州东路网长短交路结合，假设：(1)短交路到站立即折返；(2)长交路允许外段驻班，驻班时长不低于16 h；(3)不设置用餐时间窗；(4)允许乘务组在郑州站—郑州东站间采取任意形式交通工具“空乘调拨”(deadhead)[15]；(5)其余乘务规则同上例。

以郑州和郑州东动车用所27条动车交路划分的166个乘务区段为输入，各乘务规则参数如下：Np=60，[Tμ,Tμ]= [330,420], [Tε,Tε]= [15,40]，[Tτ,Tτ]=[+∞,+∞]，[Tη,Tη]= [960,1 880]，[Tλ,Tλ]= [210,300]，[Te,Te]= [+∞,+∞]，Wlun=[+∞,+∞]，Wdin=[+∞,+∞]。迭代1 000次，共求得51条乘务交路，外段驻班27次，共需78组乘务组，最优上界为269 955.00，最优下界为213 640.07，对偶间隙为20.86%，求解时间为38 279.98 s。计算结果见表3，迭代曲线见图13。

表3 郑州东路网CSP计算结果

注：OG开头的车次为乘务员“空乘调拨”。

5 结论

本文基于乘务规则提出时空节点状态坐标递推原则和乘务任务可行转化判定条件，以此为基础构建TSSN，建立基于TSSN的0-1整数规划模型。

针对模型的特点，在拉格朗日松弛框架下，将CSP松弛为时空最短路径问题集合，分别利用FDP算法和拉格朗日启发式算法求解下上界。

结果表明，TSSN配合拉格朗日松弛算法不仅可以求解发车密度大的的城际铁路CSP，而且同样适用于高速铁路网CSP。针对大规模混合时间问题而言，该方法的优势在于：(1)TSSN可以通过状态维度将一些难于刻画的混合时间约束溶解在网络中，控制网络规模，简化数学模型；(2)拉格朗日松弛算法可以将剩余“难约束”松弛，将原问题分解为若干个小规模的子问题集合，从而加速求解，并结合对偶间隙判定解的质量。故二者结合使用可以有效解决大规模混合时间问题。当然，由于CSP是具有强对称性，其松弛程度往往不便控制，从而导致下界质量难以达到最佳，所以还需要对松弛控制方法进行深入研究。