软弱围岩隧道掌子面极限支护压力研究

王秀英， 李 凯,， 王丽娟， 郑维翰， 王新东

(1. 北京交通大学 土木建筑工程学院，北京 100044； 2. 中国水利水电科学研究院 工程安全监测中心， 北京 100038；3. 铁道第一勘测设计院集团有限公司 桥梁与隧道处， 陕西 西安 710043 )

在当前隧道建设中问题最多、困难最大、风险最高的问题是软弱围岩隧道的设计施工问题。软弱围岩隧道施工具有变形量大、变形速度快且难以控制的特点，因此软弱围岩隧道施工，应坚持“加强预支护，快挖快支，及早闭合”的原则[1-2]。但是为了避免隧道开挖变形过大，往往缩小开挖断面进行分部开挖，这样不仅大型机械设备难以发挥作用，而且仰拱常常不能及时跟进掌子面，使得“及早闭合”这一原则很难实施。研究表明，掌子面超前核心土变形是导致隧道所有变形的真正原因[3]，提供及时合理的掌子面支护或加固措施，可以在全断面开挖的情况下大大减小隧道的变形，从而实现软弱围岩隧道的机械化施工[4]。因此，如何确定隧道掌子面稳定所需的支护力，成为软弱围岩隧道机械化开挖顺利进行的关键。

国内外学者对掌子面极限支护力的研究主要采用极限分析法和极限平衡法[5-10]。Leca[7]构造了隧道在砂土地层时掌子面的三维破坏模式，采用极限分析法得出了掌子面稳定的最大及最小支护力。Soubra等[8-9]在Leca的基础上改进了破坏模式，实现了掌子面前方锥形体的圆顺过渡，据此求得优化的上限解。Mollon等[10]通过理论和实验分析了隧道掌子面非对称挤出变形的失稳模型。德国B.Maidl及日本村山假定滑动面为对数螺旋线，求解得到掌子面最小支护力。黄茂松等[11]进行了非均质黏土地基隧道环向开挖面稳定上限分析。从以上的研究可以看出，相比极限分析法，极限平衡法具有计算简便，便于工程应用的优势。目前，对于土体进行极限平衡研究，往往采用费兰纽斯提出的条分法[12]，推导大部分采用竖向条分法，然而通过研究发现，竖直条分法因竖直条块与锚杆结构体存在交叉，不能真实分析整体稳定，对于应用锚杆或加筋的工程存在一定缺陷。因此，本文尝试采用水平条分法进行掌子面稳定性分析。

1 极限平衡理论掌子面分析模型建立

根据极限平衡理论，对掌子面稳定进行分析时，首先应确定掌子面前方的潜在滑动体、破裂面以及滑动模式，然后通过力学平衡原理确定维持掌子面平衡所需要的最小支护力。通过对已有研究进行调研发现，掌子面在坍塌时的破裂面最适于用螺旋线描述[4]，因此这里假设破裂面方程为

R=R0eθtanφ

( 1 )

本模型的建立采用水平条分法，条分法是将滑动土体分割为若干土条，视土条为刚体，再计算各土条上的力对滑弧中心产生的力矩。掌子面稳定分析模型见图1。

设滑裂面起始点位于θ=0处，并设螺旋线半径r0，根据相关流动法则的要求，需要令r0与水平地面夹角保持不变，应为土体摩擦角φ。滑裂面终点所对应的螺旋线半径为rh，r0与rh的夹角为θh(即：θ=θh)。q1为滑动体上方所受荷载，q2为维持掌子面稳定所需要的极限支护力。B为破裂面长度(即滑动体的纵向长度)，D为隧道高度，计算式为

D=rhsin(θh+φ)-r0sinφ=

r0eθhtanφsin(θh+φ)-r0sinφ

( 2 )

观察此模型，可以发现仅有夹角θh为变量。

1.1 水平土条力矩平衡推导

根据条分法思想，从滑动土体中任取出一条进行受力分析，见图2。土条上作用的力有重力Wi，掌子面支护力q2，滑裂面法向、切向作用力Ni、Ti，土条上下两侧法向作用力Ei、Ei+1，水平剪切力Hi、Hi+1。参考瑞典条分法推导，这时需要对土条间作用力进行假设，即不考虑两侧土体作用力，因此认为Ei、Hi的合力与Ei+1、Hi+1的合力相同，同时有相同的作用线，作用效果可以相互抵消。

依据极限平衡原理，作用在每个土条上的水平、垂直方向上的作用力平衡，可以得出微单元平衡方程为

q2hi+Ticosα-Nisinα=0

( 3 )

Ti=cli+Nitanφ

( 4 )

所以hi=risinαdθ=ricosθdθ,ri=r0eθtanφ，li=ridθ。

推导并化为

( 5 )

( 6 )

式中：c为土体黏聚力。

1.2 整体块力矩平衡推导

为了求解掌子面所需最小支护力，需要建立整体力矩平衡方程。因此，依据图2，选O点(螺旋面中心)为力矩平衡中心点，将作用在滑动土体上的所有荷载对O点求矩，令滑动土体上作用的所有荷载对O点求矩的和等于零。图2中,力矩包括：Mg、M、M、Mq2，其中Mg为重力力矩、M为q1产生的力矩、M为滑裂面荷载力矩、Mq2为q2产生的力矩。在分析中，假设抗剪强度中摩阻力、黏聚力均100%发挥作用，因此计算出的支护力较实际值偏小。

(1) 破裂面上作用力所产生的力矩M

( 7 )

(2) 掌子面水平推力所产生的力矩

由图2可知，在高度为hi的土体上，掌子面水平推力为risinαq2dθ，力臂长度为risin(θ+φ)，即

( 8 )

用MATLAB积分为

( 9 )

(3) 顶部荷载q1所产生的力矩

由图1可知，破裂面长度为

B=r0×cosφ-rh×cos(θh+φ)

顶部荷载的力臂为

即

Mq1=q1Bl=q1[r0cosφ-rhcos(θh+φ)]×

(10)

(4) 重力所产生的力矩

土块条的重力为

gi=[ricos(θ+φ)-rhcos(θh+φ)]risinαγdθ

土块条的重力臂为

rhcos(θh+φ)

采用条分方法计算重力所产生的弯矩为

(11)

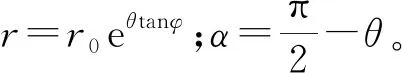
用MATLAB积分可得

(12)

根据力矩平衡，对O点力矩之和得零，得出

Mq1+Mg-Mq2-M=0

(13)

化简计为

(14)

通过对式(14)积分，可以发现求解q2的式中只有θh是未知数，通过MATLAB编程，反用最小求值迭代法，可以计算具体隧道施工所需要的掌子面支护力[13-14]。

2 计算实例及分析

2.1 隧道概况

计算实例选择宝兰客专洪亮营隧道，隧道全长961 m，起讫里程为DK988+349～DK989+310，最大埋深约120 m。洪亮营隧道地层从上自下为砂质黄土、黏质黄土，出口洞身穿越地层为第四系中更新统砂质黄土。

洪亮营隧道计划在出口端采用预切槽法施工，在切槽保护下进行全断面开挖，切槽采用中国铁建重工集团股份有限公司研制的中心轴式预切槽机械，切槽施工断面见图3，仰拱部分为采用传统开挖，图3未显示。研究主要针对埋深范围为10～50 m。为获取准确的黄土物理力学参数，在洪亮营隧道出口取原状土进行土工试验[13-14]，得到洪亮营隧道地层基本物理力学参数见表1。

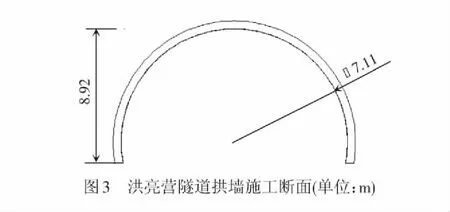
表1 黄土物理力学参数表

力学参数ρ/(kg·m-3)ω/%c/kPaφ/(°)E/kPa砂质黄土1.56×10320.8142.8222.485×104

2.2 洪亮营隧道掌子面支护力计算

根据洪亮营隧道试验段具体情况，隧道埋深取15 m，埋深与洞跨比近似为1。将表1参数代入式(14)，使用MATLAB计算得出隧道开挖需要的掌子面最小支护力为

q2=3.142×104Pa

(15)

为了检验理论计算得出的q2值是否可以维持隧道掌子面稳定，采用数值模拟方法建立埋深15 m模型，在开挖面施加支护力F，计算模型见图4[14]。

为了便于分析，取N=F/q2，计算得出掌子面挤出位移与N值的关系，见图5。当N小于1.5时，掌子面挤出位移增大趋势突然加快，且挤出位移值大于10 cm；当N大于1.5时，掌子面挤出位移较小，在5 cm之内。

对比得出，在埋深为15 m及覆跨比近似等于1范围段时采用全断面法开挖，掌子面的支护力应为1.5q2，才能确保隧道开挖安全。这也证明了在理想状态下，采用理论计算得出的掌子面最小支护力q2值较数值计算结果偏小。

2.3 不同参数影响分析

依据推导的理论公式，对不同土体参数、不同隧道埋深下，所需的掌子面支护力进行分析比较。

(1) 内摩擦角的影响

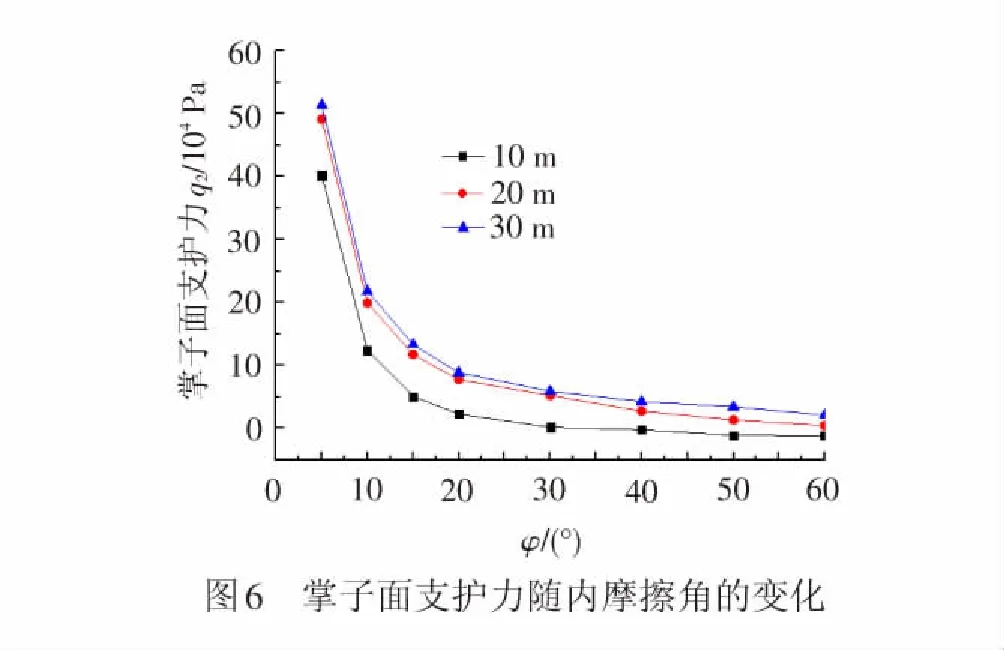
维持隧道掌子面平衡所需要的最小支护力随着土体内摩擦角的增大逐渐减小，见图6。图中负值说明增大土体内摩擦角可以提高土体自稳能力，无需支护。不同埋深隧道达到自稳所需的内摩擦角不同，当内摩擦角小于30°时，摩擦角的增大对减小最小支护力影响显著；这说明实际施工中若采用预加固掌子面超前核心土方式来提高掌子面稳定性，需要注意不同埋深下加固方案的设计，同时若采用玻纤锚杆等加固掌子面时，应注意加固密度存在合理值，并非越密越好。

(2) 土体黏聚力

随着土体黏聚力增大，维护掌子面平衡的最小支护力也近似线性减小，见图7。不同埋深隧道对掌子面支护力的需求不同，当埋深分别为10、20、30 m时，土体黏聚力需分别达到40～45、50～55、60～65 kPa，掌子面才可能达到自稳。这说明提高土体黏聚力可以减小维持掌子面稳定所需要的最小支护力，但实际若需要对掌子面超前核心土进行预注浆加固时，还需要从经济上进行分析。

(3) 隧道开挖高度的影响

随着隧道开挖高度的增大，维护掌子面平衡的最小支护力缓慢增大，当隧道开挖高度达到15 m时，掌子面支护力突然增大，随后继续缓慢增大，见图8。隧道开挖高度的增大对掌子面支护力的影响不显著，但是存在高度的临界点，本例中15 m是隧道开挖高度的一个临界点，覆跨等于1；由此可见，覆跨比为1时，掌子面所需的最小支护力会急剧增大，其后缓慢增加。

(4) 隧道埋深变化

最小支护力随隧道埋深的变化规律见图9，隧道荷载采用TB 10003—2005《铁路隧道设计规范》[15]进行计算，因此荷载随埋深增加而增大，当到达深浅埋分界后趋于稳定。

由图9可知，维持隧道掌子面平衡所需要的最小支护力与隧道荷载有相同的变化趋势，表现为最小支护力随着隧道埋深增大先增加后趋于稳定，文献[16]通过离心模型试验也得到了同样的结论。另外，从图9还可以发现洪亮营黄土隧道可以达到自稳的最大埋深介于9～10 m。

3 离心模型试验验证

土工离心模型试验的基本原理是用原型材料按一定比例尺制作模型，将其置于离心试验机中，通过加大离心加速度，加大模型自重体积力，使模型的力学状态达到与原型相同水平[17]。由于离心模型试验可以真实再现与自重应力场相似的变形过程，并能使小比例尺模型更为接近真实的应力水平，因此已经成为研究复杂岩土工程问题的重要方法，国内外学者利用离心模型试验针对软弱围岩隧道变形开展了卓有成效的研究[16,18-19]。试验主要目的是研究掌子面不同加固情况下的稳定性，进而对理论计算提供验证。

3.1 试验简介

试验在中国水利水电科学研究院离心实验室LXJ-4-450大型土工离心机上完成。该离心机设计最大加速度为300g，有效旋转半径为5.03 m，见图10，有效负载1.5 t，有效荷载容量为450 g·t，使用模型箱的有效尺寸为1.35 m×0.72 m×0.9 m(长×宽×高)，见图11。

试验以洪亮营隧道为原型，模拟其浅埋段，埋深20 m，隧道断面原型见图3，预衬砌厚度40 cm，综合考虑原型、试验箱情况及边界效应等对试验结果的影响，选定相似比n为60。根据离心试验要求，模拟围岩的材料取自洪亮营隧道现场黄土，在试验室经重塑并进行物理力学参数试验，以保证与现场土性的一致[13-14]。衬砌材料采用有机玻璃模型，依据DL/T 5102—2013《土工离心模型试验技术规程》[20]，考虑泊松比的影响，有机材料的厚度为

(16)

式中：μm、Em、dm分别为模型材料的泊松比、弹性模量、衬砌厚度；μp、Ep、dp分别为原型型材料的泊松比、弹性模量、衬砌厚度；经计算得到有机玻璃厚度12 mm[13-14]。

试验主要分析超前核心土加固对掌子面稳定性的影响，为此制作了两个模型，左侧隧道是超前核心土有锚杆加固，右侧隧道是超前核心土没有锚杆加固。试验前有无锚杆超前核心土的情况见图12。激光测试点Z1、Z2分别用来测量左右侧隧道掌子面挤出位移。

根据离心试验的操作要求，制定了不同离心加速度值下的稳定时间[14]，达到60g后稳定8 min，最终获得了不同时间段、不同离心加速度值下激光传感器的数据。

3.2 试验结果及分析

试验通过Z1、Z2激光测点测定左右两隧道掌子面挤出位移，试验中由于仪器问题，Z1测点数据未得到。试验完成后，通过对比发现左侧隧道(有锚杆加固掌子面)超前核心土保护较完整，右侧隧道(掌子面未加固)超前核心土完全破坏，见图13。这说明超前核心土的加固对保护掌子面稳定非常重要。

试验过程中Z2点位移变化曲线见图14。由图14可见，随离心机加速，掌子面挤出位移总体在逐渐增大，当离心加速度值达到17g，掌子面挤出位移达到0.12 cm，激光传感器测出的位移值骤然减小到-0.21 cm，说明掌子面坍塌，且坍塌厚度为0.33 cm左右。后期随离心机加速，掌子面挤出位移又逐渐增大，在60g时，测得的挤出位移值为0.05 cm，到达70g时，挤出位移达到0.26 cm。

分析以上试验结果：当离心加速度值达到17g，隧道掌子面发生了坍塌，按照1∶60的相似比，土体坍塌时埋深还原应为6.7～7.0 m。理论计算中，土体坍塌时的埋深为9～10 m。两者差别一方面在于理论公式是在完全理想状态下推导，假设土体的黏聚力、摩擦角100%发挥了作用，另一方面在进行试验塑模过程中，掌子面受到一定程度扰动，土体黏聚力和摩擦角都小于原状土的实际数值，因此试验坍塌埋深小于理论计算坍塌埋深是合理的。

数值计算得出将理论计算q2值的1.5倍设为最小支护力是安全的，从理论与试验的对比来看，理论计算得出的不需进行掌子面支护的埋深为9～10 m，与通过试验得出的埋深6.7～7.0 m的比值为1.285～1.492，接近1.5，可见试验结果同数值计算结果近似相同。因此，黄土隧道中，可采用本文理论计算式计算结果的1.5倍作为掌子面的最小支护力。确定了掌子面所需的支护力，就可以采取相应的掌子面稳定性控制技术，其中最为有效和适用的是掌子面预留核心土[21]，可以根据所需支护力的大小，按照土力学理论并结合隧道高度及跨度计算并优化台阶高度和宽度。

4 结论

本文通过极限平衡理论，推导了维持掌子面稳定的支护力的计算公式，依托计划进行全断面开挖试验的宝兰客专洪亮营黄土隧道，求解了试验段浅埋情况下所需的掌子面支护力，并与数值模型计算结果进行了对比，最后通过离心模型试验来验证理论分析及数值计算结果，得到的主要结论如下：

(1) 掌子面所需支护力随土体内摩擦角、黏聚力的增大逐渐减小，不同的是，支护力随黏聚力的增加基本成线性减小，而随摩擦角的变化并非呈线性关系，当内摩擦角小于30°时，摩擦角的增大对减小最小支护力影响显著，再继续增大效果不明显，另外，不同埋深隧道达到自稳定所需要的内摩擦角不同，这说明实际施工中若采用掌子面玻纤锚杆等加固时，应注意加固密度存在合理值，并非越密越好。

(2) 埋深一定时，掌子面所需支护力随隧道开挖高度增大先是缓慢增大，达到覆跨比为1时急剧增大，随后又缓慢增加。掌子面支护力随隧道埋深增大先增加后趋于稳定。

(3) 离心模型试验表明，无掌子面加固的核心土在试验过程中完全坍塌，而有掌子面加固的核心土较为完整。离心试验过程中，离心加速度值达到17g，隧道掌子面发生了坍塌，土体坍塌时埋深还原应为6.7～7.0 m。

(4) 离心模型试验较好的验证了理论计算、数值分析结果，黄土隧道中，可采用本文理论计算式计算结果的1.5倍作为掌子面的最小支护力。由于条件所限，不能进行大量的离心模型试验，因此，本文推导的理论公式也需要在实践中进一步修正。