基于谐波小波包和IAGA-SVM的滚动轴承故障诊断

吕维宗 王海瑞 舒 捷

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

0 引 言

由于工业生产的不断发展，大型复杂机械设备安全可靠的运转引起了社会的逐渐重视，相关故障诊断技术也得到了迅猛的进展。滚动轴承是大型机械设备的关键组成部分，因此大型机械滚动轴承的故障特征诊断相关技术有着十分重要的作用，而这是属于模式识别方面的问题。平时高负荷运转时产生的安全故障，安装、拆卸等多种情况下都会产生故障。所以，滚动轴承运作、维护等工作及其相关故障的诊断工作显得尤为重要。故障主要包括外圈出现裂纹、内圈点蚀、滚动体点蚀三类[1]。而以上故障是很多因素共同作用所导致的，但是故障及其成因并不是一一对应，且往往对应关系较为复杂。目前复杂机械设备故障诊断的方法中，人工神经网络和模糊综合评价法等较为常见[2-6]。后者在体现模糊观点方面效果十分突出，缺点是它设定评价因子的权重时要不断地依赖有关专家的以往经验，进而导致上述结果将产生一定程度的偏差。人工神经网络更擅长自学和对任何非线性函数有更好的逼近，并且更为形象地拟构了人类脑神经系统方面的物理结构以及多种多样的网络结构，但其在呈现模糊信息方面的表现不好，甚至相对较差[7-9]。

大型机械故障状态下的训练样本的获得，是一件非常不易的工作。原因是实际过程中能训练的样本并不多，这就导致很难展开一系列的训练，这时便有处于故障隐患样本数据出现。进行识别时选取分类器必须以这种样本数据特征来着重注意是否能对小样本展开明确分类，并且得到的分类结果有着较高的不定性。针对上述情况，文献[10-11]运用SVM方法将故障数据进行高维投影以达到确定故障产生的原因，且准确率较高。

综上所述，本文把谐波小波包和改进自适应遗传算法的SVM相结合，将滚动轴承数据用谐波小波包分解后便可知各频段的小波分解系数，获得的特征能量做相应的归一化处理后成为特征向量。把上述向量输入到SVM模型并展开训练，此时再将SVM的参数通过IAGA去优化，进而对捣固车滚动轴承故障类型进行诊断[12]。通过与其他方法对比可知此模型效率更高且更加准确。

1 相关概念

1.1 支持向量机和支持向量分类机

支持向量机是将有关统计学习的方法和结构风险的理论两者结合的方法，其处理小样本、非线性和高维的模式识别时便突显出优势[13]。它可以从有限的样本信息中学习并获取训练样本特征并展开相关预测，所以得出的结果往往有着很强的泛化能力，在处理过学习问题时，是神经网络所不能比拟的。

支持向量分类机运用支持向量机模型与复杂变换非线性相结合，对低维数据进行高维空间投影并在高维空间中产生最优分类面。SVM的核心就是将结构风险最小化的思想在分类领域中得以体现。处理线性可分的相关分类问题时,SVM可以寻出符合条件的最优超平面，分类结果距离分类界面要远，也就是空白区域最大，如图1所示。

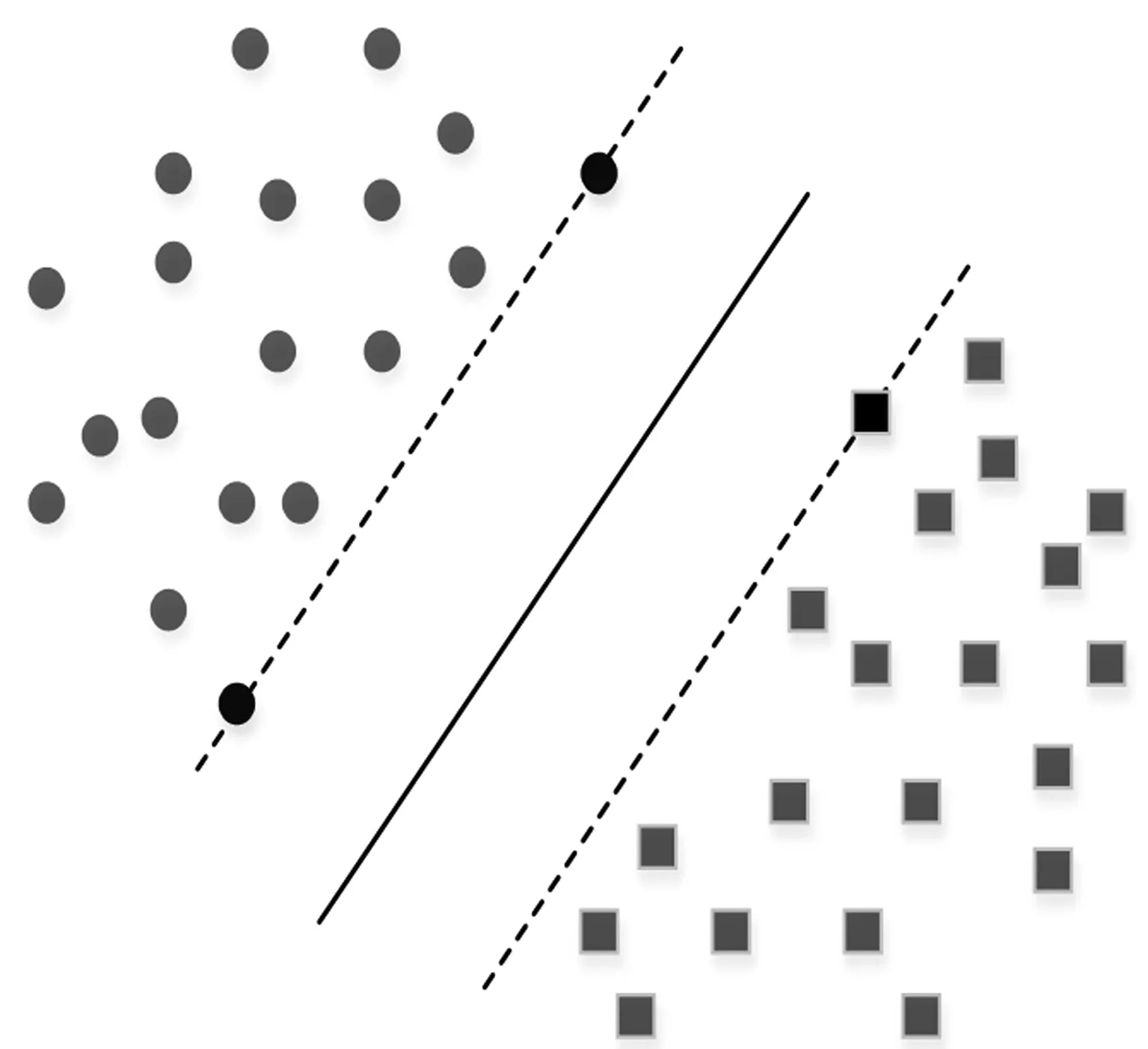
图1 SVM的最优分界面

图中圆圈和方块分别为两类样本，实线为样本分类线。两条虚线是穿过全部样本里距离分类线最近的样本点，由此可知，不仅要使两条虚线间的空白区域最大，同时还必须使两类样本能被分类样本准确区分出来。这里，ω·xi+b=0代表分类线，经归一化处理后，其对线性可分样本集(xi,yi)，i=1,2,…,l,x∈Rd,y∈{1,-1}，满足：

(1)

s.t.yi[(ω·xi)+b]≥1i=1,2,…,l

(2)

s.t.yi[(ω·xi)+b]≥1-ξii=1,2,…,l

ξi≥0i=1,…,l

式中：C>0为惩罚系数。因为往往不能找到超平面，所以只要用可以准确划分样本的所有超曲面中最优的那个来顶替超平面。但是因为超曲面并不像超平面那样存在可以间隔的特点，要找出来符合条件的超曲面的难度也比较大。因此在此类最优求解中添加能将数据从低维映射到高维特征空间的核函数K(x,x′)，再展开线性分析，便可筛选惩罚系数C>0。以下为最优求解模型：

(3)

式中：αi、αj为拉格朗日乘子，K(x,xi)为满足Mercer条件的核函数。

由此可求得分类决策函数为：

(4)

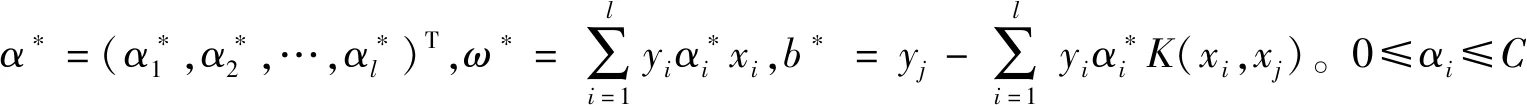
本文采用基于“一对多”算法的多值分类SVM模型，其基本思想是：对N类分类问题建立N个SVM，在每个类和余下其他类之间训练1个SVM将彼此分开。整个过程中测试样本通过所在分类器识别失败时就要再依次通过接下来的分类器，重复整个过程寻找出可以将故障识别出来的分类器并输出诊断结果。

1.2 核函数的选择

由于核函数对SVM来说非常关键，因此支持向量机的核函数及参数选择不同时会造成相关性能有着较大差别[14]。核函数构造的合理程度会对支持向量机的分类泛化性能有着很大的影响。所以在此所用的径向基核函数有助于故障分类准确度的提升。在最优求解中添加可以将数据从低维特征空间映射到高维特征空间的核函数：

(5)

用K(x,x′)代替式(4)中的K(x,xi)，此时支持向量机分类决策函数如下式：

(6)

1.3 自适应遗传算法

遗传算法把解空间用相关编码变换成相关染色体空间，把决策变量也随之变成某一结构的染色体个体并构成群体，此群体经选择、交叉及变异之后从中筛取高适应度部分用来产生下代个体，再组成下代的群体[15]。满足终止条件后遗传寻优过程结束，从而得到适应度最佳的个体，整个流程如图2所示。

图2 遗传算法处理流程

这里所涉及的交叉概率及变异概率大多是不变的，而次优解使得到最优解的时间加长。一旦遗传算法出现局部最优或全局最优时，随着交叉及变异概率的上升也将导致近似的最优解有一定损失[16]。上述原因会使遗传算法失掉很大一部分性能，所以这里选用自适应遗传算法，使用该算法后便可以根据输入值来更正交叉概率及变异概率，如下式所示：

(7)

(8)

式中:f1是两交叉个体中相对大的个体的适应度值，f2代表着变异的个体的适应度值，Pc和Pm分别表示交叉概率和变异概率，favg和fmax分别为平均适应度值、最大适应度值。这就可以极大概率地留住群体中的优秀个体，在此考虑交叉及变异的存在，所以k1及k2是提前定好的一个值且不超过1.0，它们的值根据之前经验可以设成0.4、0.1。

1.4 改进的自适应遗传算法

改进的自适应遗传算法可以针对某个解给出最佳交叉概率和变异概率。适应度比平均适应度低时就选取较大交叉率及变异率，若适应度值比平均适应度值高，则取对应的交叉率及变异率[17]。由式(7)、式(8)可得，个体适应度值和fmax近似时，交叉、变异概率越小；与fmax相等则交叉、变异概率为0。式(7)、式(8)并不完全适用于进化初期群体，相反会适用于进化后期群体。这是由于初期可基于自适应遗传算法给出改进，交叉概率及变异概率经过更改后可由下式来做调整。

(9)

(10)

式中：fmax代表最大适应度值，favg代表着平均适应度值，f1、f2各代表两交叉染色体其中相对大的一个的适应度值及待突变个体的适应度值。Pcmax、Pcmin表示最大、最小交叉概率，Pmmax、Pmmin表示最大、最小变异概率。λ为常数，一般情况下λ=2。在人工经验的基础上可令Pcmax=0.9、Pcmin=0.6、Pmmax=0.1、Pmmin=0.001。

综上所述，交叉概率及变异概率能够在染色体进行交叉变异时进行自适应调节，算法才可以寻找全局最优解，保证群体的多样性及遗传算法的收敛性。

2 谐波小波包方法

2.1 谐波小波包原理

Newland根据谐波小波的信号分析的具体特征构建出了谐波小波，并依次每层都展示出小波所处的频段，由于信号细化的原因，所有频段并不能出现在同一分解层上，所以再进行细分即可获得某部分频段。谐波小波在频域有着优良的盒形谱特性，其相应频域表达式如下：

(11)

时域内表达式可如下表示：

ωm,n(x)=[exp(in2πx)-exp(im2πx)]/[i2π(n-m)x]

(12)

式中：i为谐波小波在相应时域中的相关系数。

小波变换中的层次取决于式(12)的m、n，根据谐波小波的滤波功能可以对待分析的所需频段进行保存。

但谐波小波包的最终分析并不能进行选择，对频段的细分不能满足要求，对时域振动信号进行筛选时有局限性。运用二进制小波包细化的原理来进行无限细分的自适应分解，公式如下：

(13)

式中:B表示分析频带的宽度，等价于2-jfh；其中fh是最高频率表达式。

2.2 谐波小波包频域分布实现过程

由谐波小波核心思想可得谐波小波包的频域分析图如图3所示。

图3 谐波小波包的频域分析图

上述可知信号一旦分解到了特定程度的层，再结合m、n值就能得到频段的上下限，以下是变换算法完成的流程：

(1) 结合信号的先验知识、带宽及频段宽度将其所对应的频段值及层数求出来，频段值和层数j可从B及下式得出：

m=sBn=(s+1)Bs=0,1,2,…,2j-1

(14)

(2) 算出频段值：

(15)

(3) 对离散信号的时间序列fd(r)经快速傅氏变换处理便可得处于频域的离散值fd(ω)；

(4) 当前涉及的频段小波变换可由下式获得:

Wf(m,n,ω)=fd(ω)φm,n[(n-m)ω]

(16)

(5) 如果要对时域上的信号特征展开分析，则进行逆快速傅氏变换。

2.3 利用谐波小波进行特征提取

因为谐波小波包在进行特征提取时具有很大的优势，所以它是特征提取这一部分的良好手段。这一过程用以下步骤表示:

(1) 求小波系数，利用谐波小波包将测试数据做分解处理即可;

(2) 利用下式求出不同尺度时的小波系数能量值:

(17)

式中：N、M分别为频带个数及各频带的小波系数所拥有的数量。

(3) 将所获得的能量做如下式标准化相关的操作:

(18)

式中：mean和Dσ分别为小波频带的能量的均值及其标准差。

从而由下式可知特征向量:

(19)

谐波小波包的分解、定位能力相对强一些，它的表达式以及运算过程也比较简易，并可以更加细化分析信号的任何一个频段。

3 故障诊断模型构建

进行支持向量分类机建立时，适用的惩罚系数C及核函数参数σ显得尤为重要。而传统的经验或梯度下降法将对支持向量分类器的泛化效果造成影响[18]，而本文设计基于谐波小波包和IAGA-SVM的滚动轴承故障诊断模型。首先利用谐波小波包得到特征向量，再把特征值输入SVM模型中训练并对核函数和惩罚系数进行优化，增强 SVM分类器的泛化及学习能力，再根据其识别方法来构造相应的诊断的算法，这样才能使识别的速度和正确率得到提升。

多值分类问题是由二值分类问题提出来的，它是将多个数目的两类SVM分类器结合在一起再进行分类的。该算法首先根据改进的自适应遗传算法来设立N类故障分类器；当建立到第i个分类器的时候，将这类SVM训练样本划分成为同类，类别标号为1；接下来把上述故障之外的全部训练样本统称一类并记作-1。图4给出本文所述多值分类SVM故障诊断模型。

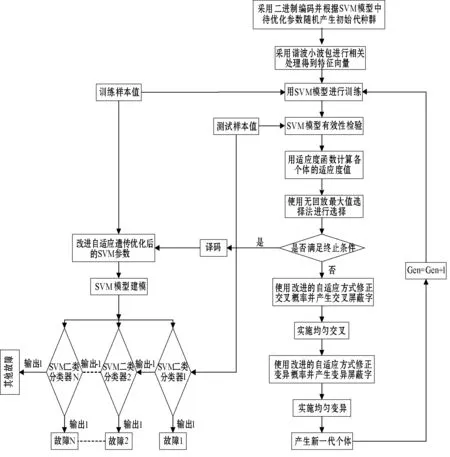
图4 基于IAGA优化的多值分类SVM故障诊断模型

综上所述，提出基于改进的自适应遗传算法优化SVM的捣固车滚动轴承故障诊断方法，过程实现如下步骤：

(1) 寻找本模型中待优化的参数，也就是径向基核函数参数σ及惩罚系数C。

(2) 确定个体编码方式，在SVM分类机中的待优化参数有两个，数量少，所以实施二进制编码可使优化搜索速度得到提升。

(3) 随机产生个体数量为M个的初代种群。

(4) 用谐波小波包处对各状态下的多组训练数据进行信号分解，计算出能量。经过归一化处理小波频带能量均值及标准差后可得各故障状态时的滚动轴承特征向量。

(5) 在训练数据集基础上对种群中全部个体在多值SVM模型中展开训练，训练样本故障类型是第i类SVM时，标号为1，反之为-1。

(6) 检验训练后的各SVM模型，并以此为依据评判种群中全部个体的适应度值。

(7) 判断是否满足算法的终止条件。若满足则转(9)，不满足转(8)。

(8) 当前种群进行无回放最大值选择、均匀交叉和变异的相关操作，转(5)。

(9) 从种群中选一个适应度最高的个体，并把该个体的表现型参数当作经过IAGA算法处理过的SVM模型的参数C*和σ*。

(10) 以优化处理后的惩罚系数C*及径向基函数参数σ*为基础，构造支持向量机诊断模型。

(11) 运用构建的SVM故障诊断模型进行诊断。

4 仿真实验及结果分析

本文选取美国西储大学的实验数据，特征提取方法为谐波小波包，其过程为: 把测试数据多层谐波小波包分解后得出各个尺度的小波系数，再算出全部尺度的小波系数能量并做相关归一化处理，求出特征向量。当故障的直径以及转速分别是7 mil和1 750 r/min时，图5为某一组时域波形。这里选用美国凯斯西储的滚动轴承数据文件，内圈故障107.mat，滚动体故障120.mat，外圈故障132.mat，正常99.mat。

(a) 正常数据时域波形

(b) 滚动体故障时域波形

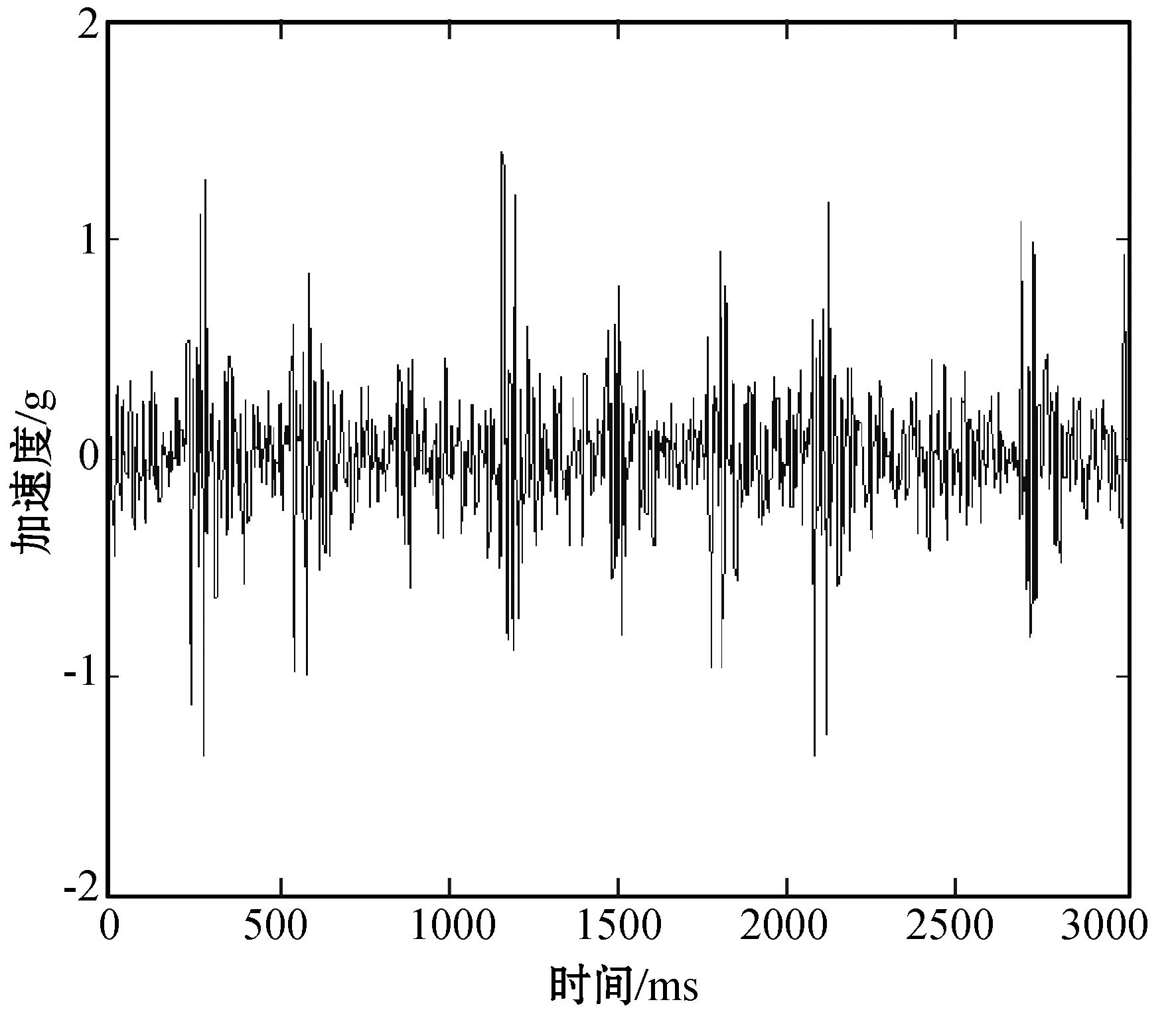
(c) 内圈故障时域波形

(d) 外圈故障时域波形图5 各种状态下的时域波形

用谐波小波包对此实验数据做相应处理操作后可得出4种不同特征能量如图6所示。

图6 不同状态的特征提取能量分布图

由此可得谐波小波包可完整细分全部分析频带，在滚动轴承故障频率特征的提取中表现得更好，因此谐波小波包提取特征时会对要诊断的故障进行更好的细分。

因此，只要将谐波小波包对不同故障下的振动信号展开分解及重构后所提取的频带能量作为特征向量输入到已构造好的IAGA-SVM模型中，便知是哪种类型的故障。这里把提取出来的故障特征分为训练样本及测试样本，将训练样本通过SVM模型训练、测试；再经过改进的自适应遗传算法去寻优得到SVM的最佳核参数σ及惩罚系数C，把测试样本输入到经过优化的SVM当中，便可知滚动轴承故障诊断的结果。此实验由100 ×4组特征样本，选取各状态下的前50组，也就是200组当作训练数据。在有了判别4种不同状态的能力的情况下，再运用剩余200组数据展开相应测试。其中的一组测试数据和判别情况如表1所示。

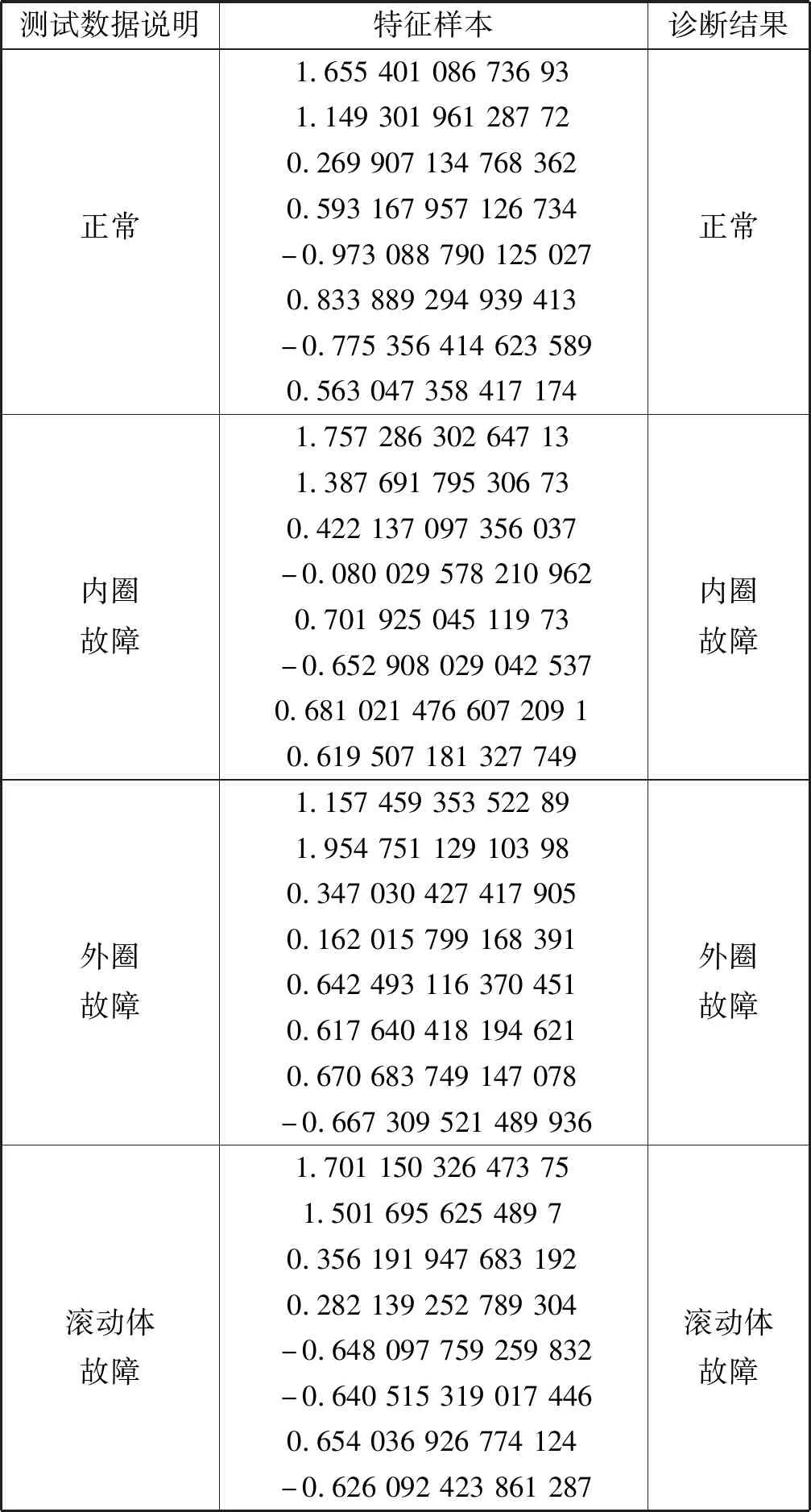
表1 捣固车滚动轴承各故障类型对应的特征样本和诊断结果

进化到最终代数就会终止寻优并记录最优参数。在此将改进的自适应遗传SVM、自适应遗传SVM、简单遗传SVM三种模型相互对比，分别将滚动轴承故障的样本数据用这三种方法做相应的处理，再根据展现出来的收敛效果及诊断误差来判断此实验中IAGA-SVM的抗变换性。图7反映出三种不同算法对SVM参数进行优化时的迭代次数和平均适应度两者的具体对应情况。图8反映出三种不同算法对SVM参数进行优化时训练的次数和误差平方和两者的具体对应情况。

图7 不同算法对SVM参数优化时的迭代次数和平均适应度的关系曲线

图8 不同算法对SVM参数进行优化时的训练次数和误差平方和的关系曲线

由图7、图8可知，用IAGA处理SVM参数时可使收敛情况呈现出的效果最好且误差最小，原始算法GA表现最差，出现全局最优的结果并不理想。确保分类准确率的同时，IAGA在第70代就可以寻找到最优值且之后基本有平缓的趋势，那么可得最优惩罚系数和核参数分别为C=0.0573、σ=0.4105。AGA和原始的GA算法还要继续进化到上百代才可以寻找出最优，且两者皆没有IAGA的好。

需要说明的是：惩罚系数C可将系统的学习能力体现出来，核参数σ体现的是样本所处的高维空间里的呈现情况的复杂程度，分类器泛化能力就与此相关。分类正确率与两者的关系如图9所示，此时核函数为径向基函数。

图9 样本分类正确率和核函数参数、惩罚系数三者之间的关系图

在图9三维曲面中可得，由于核参数及惩罚系数的取值的多样性，使得分类时的准确程度会出现局部最优的情况，恰好由于IAGA使这种情况不会存在，这展现出IAGA优良的全局寻优能力。并且因为支持向量机良好的分类识别性能使得分类正确率大多在最佳识别精度上下。因此IAGA算法和SVM的有效结合是有很大的运用价值。

将获得的最优参数运用在建立好的分类器上，从而给出关于测试样本在判别分类完成后的效果如图10所示。

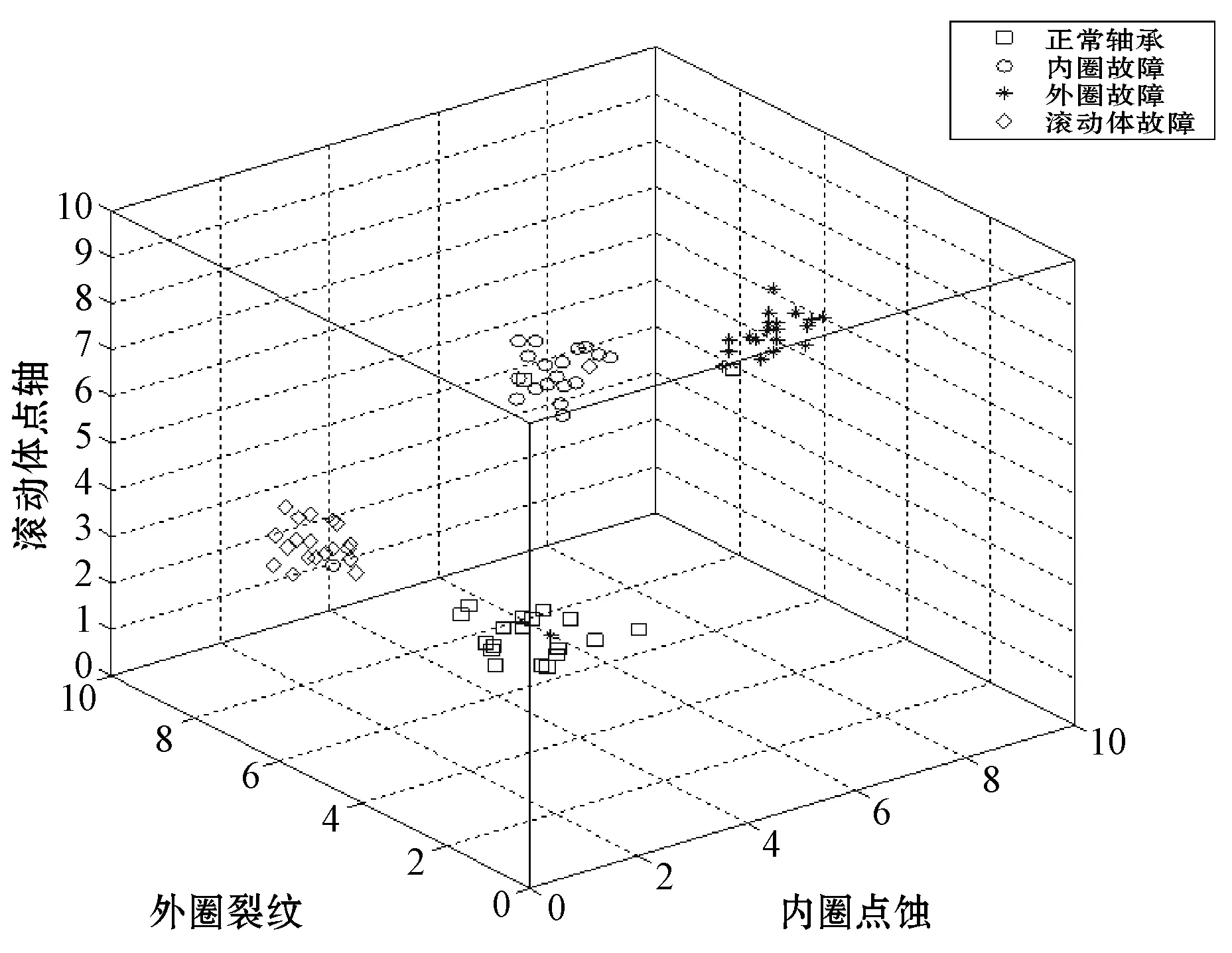
图10 IAGA最优参数建立的多值SVM分类效果图

从图10效果可以看出此模型分类效果优良且判别准度高。为了使本文所提模型更有说服力，在同样的训练及测试样本的条件下，用本文的方法与BP及RBF神经网络故障识别的效果展开对比，得出3种算法分类性能的详细对比如表2所示。

表2 三种算法分类性能比较

由表2看出，SVM参数经过IAGA寻优后的诊断准确率可以到100%，完全符合工程中所涉及的实际需求，BP和 RBF测试结果都相对较低。说明针对小样本集时SVM的分类性能要强于BP及RBF神经网络，且小样本问题可用本文提出的模型展开处理。

5 结 语

本文将谐波小波包在特征提取方面的优良性能、IAGA出色的全局寻优能力以及SVM在模式识别时展现出的优良性能相结合。用改进的遗传算法对SVM模型中的参数做自适应优化，再根据多值SVM模型对捣固车滚动轴承故障进行分类，可提升诊断精度、效率及泛化性能。实验表明，谐波小波包有着将所有分析频带细化的特性，且本文所提出的IAGA-SVM捣固车滚动轴承多值诊断技术相对AGA-SVM和GA-SVM可以更迅速寻找出最优参数，同时其诊断结果相对BP及RBF神经网络准确性更高，可靠性更强，抗变换性也更强。所以此模型有着突出的优越性以及实际运用价值。