基于算符正规乘积的拉盖尔多项式与厄米多项式关系推导

万志龙，王刚，李恒梅，黄红云，王震

(常州工学院理学院，江苏常州213032)

0 引言

厄米多项式和拉盖尔多项式是量子物理学中的两个非常重要的特殊函数，在量子光学、数理方程中也有广泛应用[1-3]。例如厄米多项式与量子谐振子的波函数、坐标本征态等有关[4]，拉盖尔多项式与氢原子、类氢原子和碱金属原子体系的能级和径向波函数有关[5]，在量子光学中，厄米多项式态的非经典性质一直是热门的研究课题[6]。文献[7]通过厄米方程和拉盖尔方程之间的联系，得到了厄米多项式和拉盖尔多项式的关系，但推导方法过于抽象，并未给出拉盖尔多项式的递推关系，对量子力学初学者有一定难度。本文利用算符正规乘积的性质，从算符厄米多项式的定义出发，推导出拉盖尔多项式和其母函数形成、厄米多项式之间的关系，并且给出了拉盖尔多项式的递推关系。此方法简捷明了，有助于学生在学习量子力学时加深对厄米多项式和拉盖尔多项式的理解，帮助学生拓宽学习思路。

1 算符正规乘积性质简介

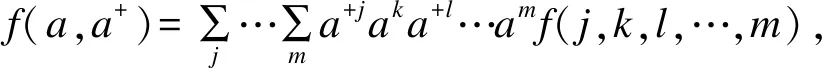
2 推导拉盖尔多项式的关系式

在数学上将e2λx-λ2按λ的幂级数展开，即可得到厄米多项式的母函数

(1)

将式(1)中的自变量x用坐标算符X来代替，就可以得算符厄米多项式的母函数

(2)

利用正规乘积的性质和Baker-Hausdorff算符公式[8]，不难得到两个有关算符厄米多项式的恒等式[9]

Hn(X)=∶(2X)n∶

(3)

和

Xn=(2i)-n∶Hn(iX)∶

(4)

根据数理方程泰勒级数展开理论和式(3)，容易得到

(5)

(6)

(7)

(8)

为了得到拉盖尔多项式的具体形式，我们不妨采用待定系数法，将式(8)幂级数展开

(9)

其中Ln(X)为待定算符多项式，比较式(8)和式(9)中的tn系数，可得

(10)

再利用式(3)，得到

(11)

再将式(11)中的动量算符X用经典数x代替，恰好就是拉盖尔多项式的原始定义式

(12)

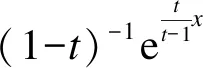
(13)

上述推导过程是以厄米多项式的母函数为出发点，由此可见厄米多项式和拉盖尔多项式之间必然存在某种联系，接下来我们将利用量子力学中坐标表象完备性关系推导两者之间的关系。

3 推导厄米多项式与拉盖尔多项式的关系

进一步将式(13)推广为伴随拉盖尔多项式的母函数(推导过程见附录)

(14)

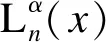
(15)

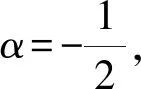
t=λ，得到

(16)

(17)

(18)

比较式(18)，可得新的算符恒等式

(19)

再借助式(4)，可得

(20)

最后将式(20)中的算符iX替换成经典数x，即可得到厄米多项式与拉盖尔多项式的关系

(21)

可以看出，这样可以非常方便快捷地推导出厄米多项式与拉盖尔多项式的关系。

4 推导拉盖尔多项式的递推关系

利用算符恒等式H2n(X)=22n∶X2n∶，将其代入式(21)即可得到式(19)的反演形式

(22)

再次利用坐标表象完备性和有序算符内的积分技术可得

(23)

另一方面，利用式(14)可得

(24)

联立式(23)和式(24)可得

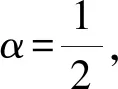
(25)

再将式(25)左边进行幂级数展开得到

(26)

比较式(26)中两边tn的系数得到

(27)

将式(27)与式(22)结合，可得算符拉盖尔多项式的递推关系

(28)

最后将算符用经典数取代，即可得到拉盖尔多项式的递推关系

(29)

由此可见，利用算符多项式方法，可以方便地讨论厄米多项式函数和拉盖尔多项式函数的性质。

5 结论

本文从厄米多项式的原始定义出发，利用算符正规乘积的性质，借助坐标表象完备性和有序算符内的积分技术，简洁明了地推导出了拉盖尔多项式，在此基础上，进一步导出了厄米多项式与拉盖尔多项式的关系和拉盖尔多项式的递推关系。另外，利用量子力学中的表象完备性，也可以将一些特殊的算符表达式展开成厄米多项式或拉盖尔多项式，从而得到一些新的公式。

附录：推导伴随拉盖尔多项式

利用式(3)得

(30)

(31)

(32)

再将式(32)左边以zn展开，可得

(33)

比较式(32)和式(33)中zn的系数，可得

(34)

再利用算符厄米多项式恒等式(3)，得到

(35)

即可得到伴随拉盖尔多项式的定义式

(36)