沈有鼎的“纯逻辑演算”思想源流——纪念沈有鼎先生逝世30周年

刘新文

(中国社会科学院 哲学研究所， 北京 100732)

作为我国较早从事数理逻辑研究的逻辑学家，沈有鼎先生(1908—1989)在数理逻辑方面所做的工作主要是逻辑演算，其成果体现在《初基演算》[1](1957年)和《“纯逻辑演算”中不依赖量词的部分》[2](1981年)两篇论文之中。前者发表之后，莫绍揆先生(1917—2011)、刘壮虎先生等著名逻辑学家对其进行了后续研究(1)莫绍揆先生认为“沈有鼎先生的初基演算，可以说是用直觉主义的眼光来讨论模态系统，也可以说是用模态的观点来推广直觉主义系统。这是一个新尝试，是一条很可继续研究的道路”。莫先生在公理的选择上对初基演算加以改进，提出了3个改进的初基演算系统，参见文献[3]第134-136页。2000年，刘壮虎先生建立了初基演算的邻域语义学并证明了对于这一语义的完全性定理，参见文献[4]第258-267页。；后者是《个体与真值的演算》(英文未刊稿)的主要内容，至今研究者甚少。1995年，先师张清宇先生(1944—2011)将《个体与真值的演算》译为中文发表在文集《理由固然》中[5]，而作为原文的英文版则发表于2000年的文集《摹物求比》中[6]；张尚水先生在1998年的综述性论文中记录了该文的大致写成时间(2)1998年，张尚水先生提到：“《‘纯逻辑演算’中不依赖量词的部分》是沈先生在60年代初期用英文写成的长篇论文《个体与真值的演算》的主要部分。在《个体与真值的演算》中还有更多的内容和结果。”参见文献[7]。。

沈有鼎关于不带量词的“纯逻辑演算”具有很多漂亮的性质，是从带等词的一阶逻辑中分离出来的一个完全的、可判定的子系统。本文拟探讨它的时代背景、它所研究的问题和思想在20世纪四五十年代丘齐(A.Church，1903—1995)工作中的直接来源及其对后来研究者的影响，并沿着其中的一个方向做进一步推进。

一、无量词“纯逻辑演算”的主要内容

根据张尚水的记录，《个体与真值的演算》完成于20世纪60年代初期，《“纯逻辑演算”中不依赖量词的部分》是其主要部分。我们以正式发表的后者为主，结合两篇论文来概述其主要内容和思想。

沈有鼎建立的这个演算以外延为出发点，把函项与谓项看成是具有同等逻辑地位的对象，5个基本概念分别为：T、F、三元联结词“条件析取(conditioned disjunction)”〔A，B，C〕、等词x=y以及“杂函项”〈x，A，y〉。这里的小写字母用作个体变元，而除了T、F意指真值“真”和“假”之外，大写字母都表示真值变元。自由变元包括个体变元、真值变元和谓项变元，而约束变元不再出现，也就是说，这里定义的语言是带等词的一阶逻辑的一个不含量词的片段。

在这些基本概念之中，作为三元联结词的“条件析取”〔A，B，C〕在自然语言中表述为“如果B，那么A；否则C”(相当于英语中的表达式“A，if B，otherwise C”)，或者用经典命题逻辑的4个基本联结词定义为：(B→A)∧(﹁ B→C)或(B∧A)∨(﹁ B∧C)；“条件析取”是一种称之为“连项”的真值函项，即从真值到真值的函项。等词x=y是一个二元谓项，表示的是“个体x就是个体y”；谓项是从个体到真值的函项。“杂函项”是从个体和真值到个体的函项，在〈x，A，y〉中，当A取T为真值的时候，它的值同于x，当A取F为真值的时候，它的值同于y；“杂函项”是沈有鼎新引入的基本概念，所以他说“本系统的逻辑常项中，除了真值函项以外，基本概念不止‘同一’概念(=)，还加了一个”[2]，这里所说的“加了一个”指的就是“杂函项”。

对于添加“杂函项”的原因，我们稍作疏解。个体与真值的函项演算包含6种情形，它们分别是：(1)从真值到真值的函项(称之为“连项”)；(2)从个体到真值的函项(称之为“谓项”)；(3)从个体和真值到真值的函项(称之为“杂谓项”)；(4)从真值到个体的函项(称之为“序项”)；(5)从个体到个体的函项(称之为“狭义函项”，简称“函项”)；(6)从个体和真值到个体的函项(称之为“杂函项”)。“为了始终如一地保持我们的外延观点，我们将把连项、杂谓项、序项和杂函项都看成具有跟谓项和函项同等的逻辑地位的对象”[8]97，而“杂函项”作为基本概念在引入之后，根据其语义解释，它与其他4个基本概念就形成了表达完备的基本概念集合；因此，在这个演算中，函项完备性定理是成立的[2]，[8]97-100，证明如下：

﹁A〔F,A,T〕A→B〔B,A,T〕A∧B〔A,B,F〕A∨B〔T,A,B〕A↔B〔A,B,﹁A〕x≠y〔F,x=y,T〕[x,y,z,v]〈x,y=z,v〉α(x,y,z)[x,x,y,z]β(x,y,z)[x,y,z,z]γ(x,y,z)α(x,y,β(x,y,z))ε(x,y,z)[x,y,z,β(y,x,z)]δ(x,y,z)α(x,y,ε(x,y,z))

这些关于一元联结词和二元联结词的定义都是如下意义上最简单可能的定义[9]134：互相对偶的联结词的定义也相互对偶，而否定的定义是自我对偶的。

在上述句法和语义的基础上，沈有鼎不带量词的“纯逻辑演算”以“值表”的方式给出，而不是像通常那样列出公理和推演规则来建立推理系统。他指出，该系统采用的判定方法类似于命题演算中运用真值表判定一个公式是否为定理的方式，在这个系统中，连项的值表就是通常的命题联结词的真值表，而每一个在系统中可以定义的谓项、杂谓项、函项、杂函项都有自己相应的值表。根据其中给出的逻辑解释，“‘纯逻辑演算’中不依赖量词的部分”中的这个系统是完全的，虽然它是带等词的一阶逻辑演算中极其微小的部分。

二、思想来源及影响

沈有鼎的《个体与真值的演算》和《“纯逻辑演算”中不依赖量词的部分》的主要内容，在于给出“带等词的一阶逻辑”的一个片段(或称“部分演算”)，这个片段是可判定的，而且给出了判定过程。这些工作在那两篇论文中都没有说明任何时代背景和问题来源，我们现在把其中使用的三元联结词“条件析取”以及所述问题的来源稍加追溯。

1948年，丘齐给出了一个三元联结词的真值表并使用“[p，q，r]”来表示这个联结词，把它读作“p或r，取决于q或非q”，这就是“条件析取”名称的来源[10]87。这个括号记法源自鲍施(A.F.Bausch)的建议[10]89，给与对偶化相关的工作中带来了便利。然后，丘齐证明了以下函项完备性定理：“条件析取、t和f是命题演算独立初始联结词的完备集合”[9]131，[10]88，其中的t和f是命题常项，或称零元联结词，而且这个集合还具有自我对偶性[9]133，[10]89。在此之前，波斯特(E.Post,1897—1954)对命题演算独立初始联结词的完备系统做过系统的处理。初版于1944年、修订版于1956年出版的《数理逻辑导论(第一部)》在第24节“命题演算的初始联结词”中考察的唯一一个三元联结词就是这个“条件析取”[9]161。丘齐的这部教材是数理逻辑史上的名著，产生过广泛而深远的影响，半个多世纪以来一直在修订印行，我国的很多数理逻辑学家则直接受教于它。胡世华在20世纪60年代写成、后由陆钟万整理出版的《数理逻辑基础》介绍了这个“条件析取”函项[11]；1963年，沈有鼎指导周礼全、张尚水、诸葛殷同、宋文淦等人学习这本书[8]380，而《“纯逻辑演算”中不依赖量词的部分》的完整版本《个体与真值的演算》正是在这一时期完成的。沈有鼎的这(两)篇论文提到，“已经知道，所有的连项都可用T、F、〔A，B，C〕来表示”[8]106，这个结果直接来自于丘齐的《数理逻辑导论(第一部)》；然后，沈有鼎做了进一步推广，以大量的篇幅证明了“不仅所有的连项可用T、F、〔A，B，C〕、x=y和〈x，A，y〉来表示，而且所有可由真值表表示的谓项、杂谓项、函项和杂函项也都可用它们来表示”[8]116。

丘齐在《数理逻辑导论(第一部)》中并没有为T、F和〔A，B，C〕建立起公理系统，而是提出了以下这个问题作为习题(25.16)：“令初始联结词为条件析取、t和f。令推演规则为替换规则和以下规则：从[A，B，C]和B推出A。建立一些公理，使得所得系统对于命题演算来说是足够的。尽可能简化每一条公理，然后减少它们的数量(不计对偶)”[9]139，并且在脚注中说明“这个习题不能当做通常意义上的习题，而是作为一个尚未解决的问题留作研究之用。作者还没有试图找到解决办法”[9]139。沈有鼎建立了自己的系统，并且认为这个“系统采用一种和命题演算中运用真值表判定一公式是否定理的方法相类似的判定方法，而这个方法本身就可以理解为一种公理系统”[2]。判定问题是数理逻辑的核心问题之一；20世纪初，希尔伯特在数学基础研究中提出形式主义纲领，致力于通过有穷多一阶公理来对各种数学分支进行公理化。原则上，这样的公理化把数学命题的证明归约为在一个指定的形式逻辑系统中执行一种机械的推导，在这样的情况下，判定问题尤其重要。另一方面，沈有鼎并没有停留在丘齐的这个问题上，他的系统在命题演算的基础上做了扩充，以包含等词、谓项、杂谓项、函项和杂函项。此外，“既然本系统是可判定的，那么在原则上可以把所有定理都规定为公理，同时不要任何推理规则”[2]。不过，他也提到，在这个演算中引进全称算子而把它扩张成带等词一阶谓词演算的一个相替代的演算时，考虑到丘齐的著名结论，即一阶逻辑不是可判定的，“当然就不可期望仍有一个能行的判定过程，因此在这情形下有一个公理系统就相当必要”[8]132，只是这个想法没有继续讨论。

至此我们已经看到，在沈有鼎建立的“纯逻辑演算”中，条件析取“〔A，B，C〕”和杂函子“〈x，A，y〉”都作为初始概念出现，前者的括号记法承续自丘齐等人的工作，后者是沈有鼎“引进的新概念”[8]99。此外，通过定义引进的杂函项[x，y，z，v]、α、β、γ、ε和δ都采用了方括号记法。这些初始概念中的括号兼具了括号和联结词的作用，随后，沈有鼎的弟子张清宇研究了这些工作，对括号记法做了进一步发挥。

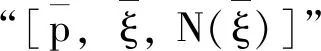
三、条件析取的后承系统

为建立条件析取、t和f这3个经典命题逻辑联结词的后承演算系统，我们首先把丘齐所给经典命题逻辑语言中的公式整理如下：

α∷=p|f|t| [α,β,γ]

公式的语义解释在前面已经给出。后承演算系统由以下5条公理和规则组成：

公理1(Id公理)：

p,Γ⟹Δ,p

公理2(f公理)：

f,Γ⟹Δ

公理3(t公理)：

Γ⟹Δ,t

规则1(括号引入规则1)：

规则2(括号引入规则2)：

这个系统的可靠性和完全性定理证明的具体细节，以及与沈有鼎不带量词的“纯逻辑演算”系统相关的其他工作(如公理系统等)将在另文详述，此处不赘。

四、结语

沈有鼎先生在20世纪60年代所建立的不带量词的“纯逻辑演算”接续了丘齐、波斯特在20世纪四五十年代的工作，这些成果不仅丰富了经典的判定问题，而且丰富了函数代数领域。对于本文提到的各种未解决问题，我们将在另外的工作中做进一步研究。

致谢：马明辉教授在本文尤其是第三节的写作过程中提供过具体的意见，特此感谢！