K12阶段学生计算思维评价工具构建与应用*
2019-10-17白雪梅顾小清
白雪梅,顾小清
(华东师范大学 教育信息技术学系,上海 200062)
一、引言
随着信息技术的迅速发展以及21世纪技能运动的普及,社会对人才的培养提出了新要求,计算机思维(Computational Thinking)受到了各国的高度重视。澳大利亚、美国、英国、芬兰、新西兰、韩国等国家为了推动K-12阶段计算思维教育,都先后发布了相应的政策文件。英国政府于2013年11月发布了计算课程的目标框架,计算思维是其核心概念和主要内容。新西兰于2011年将计算机科学列为高中的必修科目。国际教育技术学会(ISTE)和美国计算机科学教师协会(CSTA)认为所有的学生都应该在高中毕业时具备计算思维的基本技能,应将计算思维纳入正式教育,并要求各年级的所有内容领域的教师为培养学生的计算思维能力做出努力[1]。我国2017 新版高中信息技术课程标准也将计算思维列为该学科核心素养之一,并且计算思维是信息技术学科核心素养培养的核心议题[2]。
不同学者从不同的视角对计算思维提出了不同的定义。周以真教授将其概括为“利用计算机科学的概念解决问题、设计系统和理解人类行为”的一种方式[3]。ISTE和CSAT认为计算思维是一种解决问题的过程,包括(但不局限于)以下几个特征:以一种能够使用计算机和其他工具来解决问题的方式表述问题;有逻辑地组织和分析数据;通过抽象表示数据;通过算法思维形成自动化问题解决方案;识别、分析和实施问题解决方案以实现步骤和资源最有效的结合;将解决问题的过程推广到其他类似问题的解决中[4]。Özgen则将计算思维定义为拥有能够使用计算机解决生活中实际问题的知识、技能和态度[5]。任友群教授等认为计算思维是一种独特的解决问题的过程[6]。
虽然目前计算思维还没有一个统一的定义,但其重要性日益凸显。周以真教授认为计算思维是除读、写、算之外每个青少年都必须具备的一项基本能力,是一种人人都应具备的基本技能,而不仅仅是计算机科学家[7]。我国教育部也指出“中小学计算机教育发展聚焦信息技术,应从小培养学生的信息意识和计算思维”[8]。对学生进行计算思维能力培养的目的不是让学生成为计算机科学领域的专家,而是让每位学生都意识到并且可以将他们的计算思维技能习惯性地应用到其他课程中[9]。信息时代要求人应该学会使用数字化工具解决问题。然而人类在解决问题的过程中,最重要的就是思维方式。因此,如何通过计算机以及其他技术工具培养学生的思维方式尤为重要。越来越多的研究者开始关注计算思维,特别是教育技术领域的专家,从21世纪技能的角度出发,认为计算思维为儿童观察和理解周围世界提供了一个新的视角,是一种利用“计算”的过程和方法理解和解决问题的新能力,也是儿童应对未来竞争和挑战的必要技能[10],应该从小培养[11],有助于学生尽早的使用计算思维技能解决现实生活中遇到的问题[12]。范文翔等人通过对国内外计算思维的研究进行文献综述发现当前国内计算思维的研究还处于初级阶段,计算思维的应用研究层面主要集中在高等教育阶段,主要聚焦于计算思维的培养策略等。而国外相关研究已处于成熟的早期阶段,应用研究主要集中在K12阶段,并且主要关注计算思维的培养以及评价[13]。
评价对于计算思维的发展至关重要,是培养学生计算思维能力的基础也是对培养成果进行评估的重要手段。然而,目前国内尚无科学的权威的K12阶段学生计算思维能力的评价工具。国际上,Korkmaz等人根据ISTE给出的计算思维的理论框架,开发了测量K12阶段学生计算思维的量表(Computational Thinking Scale,简称CTS)。然而英文版的CTS能否与我国的教育文化相适宜?是否可以有效地测量我国K12阶段学生计算思维水平?因此,本研究的目的是将英文版计算思维量表引用到我国的教育情境中,探讨其对我国K12阶段学生计算思维能力测量的有效性及适用性,旨在为我国中小学学生计算思维的培养、评价以相关研究提供一个科学的工具。
二、计算思维评价框架与测量量表
(一)计算思维评价框架
ISTE将计算思维划分为创造力(Creativity)、算法思维(Algoritmic Thinking)、批判性思维(Critical Thinking)、问题解决(Problem Solving)、合作(Cooperativity)及交流技能(Communication Skills)。ISTE认为计算思维能同时反映以上五种技能,这些技能相互联系。当这些技能共同相互作用时,便解释了一种全新的思维技能——计算思维。
首先,(1)创造力需要创造性的思维,而创造性思维并不是独自发挥作用,它还涵盖了自身的内部思维结构,如批判性问题解决能力。具有创造性思维的个体同时也具有批判性思维和解决问题的能力,发展不同寻常的想法及方法是问题解决和创造力的结果,而编程是一个使得问题数值化从而有助于问题解决的过程。因此,创造力是计算思维的重要组成之一。(2)一个能够以“算法”的方式思考问题的人,在解决问题的过程中,能以一种详细而有目的的方式进行思考,通过将问题解决过程按顺序排列来实现,最终为问题的解决提出一个方案。因此,算法思维也是计算思维的重要组成之一。(3)对同一个问题的解决往往会有多种方案,需要通过批判性的思考从众多方案中选择出一个最优的方案,从而使得问题得到恰当的解决。因此,批判性思维也是计算思维的重要组成之一。(4)克服未来生活中遇到的问题是教育的首要目标之一,而计算思维是个体问题解决能力的延伸。解决问题所需的过程应该被收集并用于问题的解决,然而程序设计过程是一个典型的问题解决过程。因此,问题解决能力是计算思维的又一重要组成元素。(5)21世纪的个体为了共同的目的,具备不同的技能的个体需要通过合作解决复杂问题。(6)除此之外,在合作的过程中,成员之间要有良好的沟通来共同努力以达到问题解决的目的。因此,合作和交流技能是计算思维的另外两项重要组成[14]。
(二)计算思维测量量表
Korkmaz等人根据ISTE对计算思维的理论框架分析,结合前人的相关研究成果,开发了具有六因子结构的测量学生计算思维的量表。但是通过因子分析最终只得到五个因子:创造力、算法思维、批判性思维、问题解决能力以及合作技能。研究者通过验证性因子分析对五因子结构的量表进行了验证,各模拟指标皆达到显著。一方面,研究者通过对各因子的测量指标进行进一步分析发现,沟通交流能力的测量指标同时与批判性思维、问题解决和合作学习的大部分测量指标在本质上有重叠。另一方面,理论上,沟通交流可以简单地定义为人们分享情感、思想和信息[15]。因此,沟通交流技能其实是合作学习、批判性思维和问题解决发生的基础[16]。鉴于此,五因子结构的计算思维量表最终被研究者所接受。
研究者最终得出的具有5个因子29个测量指标的CTS的主要测量对象是大学生。后来Korkmaz等人对其进行了修订,使得其适合测量K12阶段学生的计算思维能力水平。修订之后用来测量中学生计算思维水平的CTS还是包含原来的5个因子,但只有22个测量指标[17]。
三、研究设计
(一)研究对象
一方面,由于最原始的英文版的CTS量表最初主要用于测量大学生的计算思维水平,研究者在其基础上删除了7个不适合测量K12阶段学生的测量指标,形成了测量K12阶段学生计算思维水平的量表,而高中生和大学生比较接近。另一方面,由于计算思维能力的培养已经纳入我国高中信息技术课程目标。因此,为了保证量表的适用性,本研究选取高一和高二的学生为研究对象,一共有1015名中国学生参与了研究。其中356名被试来自我国南方某省,659名被试来自我国西部某省。其中,高一的学生有379(37%)人,高二学生有636(63%)人。男生总共467(46%)人,女生总共548(54%)人。
(二)研究工具
本研究以Korkmaz等人设计开发的具有22个测量指标的CT量表为研究工具。为了确保翻译的准确性,研究采取了回译翻译法(Back-translation Method)。回译翻译要求将翻译好的目标语言再重新翻译成原文,通过对比原文和回译文,来确定译文是否存在问题[18]。因此,本研究邀请了两位精通英语和汉语的教育技术学专家。首先,请其中的一位专家先将英文版本的CT量表翻译成中文。然后请另外一位专家将第一位专家翻译好的中文版的CT量表回译成英文。最后,我们将第二位专家回译的英文版本的CT量表和原始的英文版本的CT量表进行对比,发现两个版本的量表的语言表述几乎一致。另外,最终翻译好量表还是遵循原始CT量表的计分方式,采用李克特五点计分法。
(三)数据收集与预处理
1.数据收集
将最终确定好的CT量表编辑到问卷星中,并且通过指导语向研究对象说明调查数据仅用于研究,调查题目均没有对错好坏之分,只需要凭借自己的经验和感受进行填写即可。然后将编辑好的电子CT量表的链接发送给了研究对象,开始收集数据。数据收集时间为2018年5月21日至2018年6月4日。
2.数据预处理
通过预处理发现整体样本数据没有出现缺失值和异常值。随后使用SPPS21.0将数据随机分成了两个样本,第一个样本(n=487)数据用于探索性因子分析,第二个样本(n=528)数据用于验证性因子分析。
四、数据分析
(一)描述性分析
研究首先对中文版的计算思维量表的22个测量变量进行了描述性统计分析,结果显示该量表的所有测量指标的峰度均小于临界值5,这说明数据呈正态分布。
接着研究对每个因子和其包含的测量指标之间的相关关系进行了分析,分析结果如表1所示。由表1可知,第一个因子(C)与其所含测量指标之间的相关系数在0.632-0.691之间,第二个因子(A)与其所含测量指标之间的相关系数在0.682-0.779之间,第三个因子(O)与其所含测量指标之间的相关系数在0.730-0.833之间,第四个因子(T)与其所含测量指标之间的相关系数在0.643-0.817之间,第五个因子(P)与其所含测量指标之间的相关系数在0.654-0.737之间。

表1 各因子与其测量指标之间的相关性
另外,研究对测量数据进行相关分析和独立样本t检验,发现各测量指标与总分的相关系数在0.329-0.617之间,均达到显著水平(P<0.001)。研究对高分组(前20%)和低分组(后20%)的样本在22个测量指标上的得分进行独立样本t检验,发现两组样本在每个测量指标上的得分均存在显著差异(P<0.001),说明所有测量指标之间均具有较好的区分度。
(二)探索性因子分析
研究使用SPSS 21.0对数据进行了探索性因子分析。结果显示:KMO=0.850,Bartlett's 球形检验χ2(487)=3096.258,p<0.000。根据Kaiser决策标准,如果KMO≥0.8,说明Bartlett球形检验达到了显著水平,适合做探索性因子分析。
研究采用主成分分析法抽取因子,选择最大方差法进行旋转,以特征根大于1作为判断因子个数的标准。对于各因子的取舍,以因子负荷大于0.3为标准。研究结果显示:各因子的测量指标是因子负荷均大于0.3,但有一个测量指标出现了交叉载荷,为了获得一个更好结构的量表,研究删除了该测量指标(P6),剩余21个测量指标均保留。
研究对剩下的21个测量指标的CT量表进行第二次探索性因子分析,结果显示:KMO=0.847,Bartlett's 球形检验χ2(487)=2864.603,p<0.000。同样采用主成分分析法抽取因子,用直接斜交旋转法进行旋转,最终抽取出来五个因子,分别是:合作学习、问题解决、批判性思维、算法思维和创造力,累积解释总变异的55.524%。每一个因子的解释率分别为:合作学习是24.688%,问题解决是10.707%,批判性思维是8.298%,算法思维是6.435%,创造力是5.395%。五个因子的特征根都大于1,特征根的值依次是:5.185,2.284,1.743,1.351,1.133。
(三)验证性因子分析
本研究使用LISREL软件对第二个样本(n=528)数据进行验证性因素分析,分析结果如下图所示。考察测量数据与CT量表五因子结构模型的拟合程度。参照如下拟合指标:χ2/df<3,CFI>0.9,GFI>0.9,IFI>0.9,NFI>0.9,RMSEA≤0.08。结果显示:χ2=1245.995,df=496,χ2/df=2.463,IFI=0.95,CFI=0.95,NFI=0.92,GFI=0.905,RMSEA=0.053,说明CT量表五因子结构模型能很好地拟合数据。另外,21个测量指标的标准化因子载荷从0.42到0.82。

验证性因子分析模型图
(四)效度检验
1.聚敛效度检验
模型的所有测量指标的标准化因子负荷值均在0.42-0.82之间,这表明所有测量题目都具有良好的聚敛效度[19]。因子的组合信度一般要求0.6以上[20],组合信度越大,表示测量指标之间的关联度越大,即测量指标的同构性越好。
根据模型中每个因子的测量指标的标准化因子负荷值以及测量指标的误差方差,利用计算公式[21]:

得到各因子的组合信度值分别为:创造力C(0.58),算法思维A(0.73),合作能力O(0.80),批判性思维T(0.75),问题解决P(0.73)。除了因子1,其余4个因子的组合信度值均大于0.6,说明大多数因子的测量指标均具有良好的同构性[22]。标准化因子负荷值和组合信度值均表明该测量量表具有良好的聚敛效度,测量指标可以有效反映对应的因子(潜在构念),测量同一因子(潜在构念)的测量指标的内部一致性可以接受[23]。
2.区分效度检验
研究对CT量表的5个因子进行两两组合,得到10个CFA假设模型。再将每个CFA假设模型的两个因子间的协方差分别设置为1和自由估计参数,得到受限模型Ma和未受限模型Mb,然后用ML法对模型Ma和模型Mb进行验证性因子分析,得到模型的χ2、df值及其差异量,结果如表2所示。由表2可知,5个因子的受限模型与未受限模型间的卡方值差异量均大于因子区别效度检验临界指标χ20.05=3.841,表示所有受限模型与未受限模型间的卡方值差异量均在0.05上达到显著性水平,说明CT量表中5个因子间所表示的潜在特质具有显著区别,这表明CT量表任何两个因子之间具有良好的区分效度[24]。

表2 各因子区分效度检验摘要
(五)信度检验
1.克伦巴赫值检验
本研究采用Cronbach α 系数检测量表的信度,并参照标准:如果α>0.8,表示量表的信度良好;如果0.7<α<0.8,表示量表的信度可以接受。分析结果显示(如表3所示):合作学习、问题解决、批判性思维、算法思维以及创造力的Cronbach α依次是0.805、0.734、0.736、0.727、0.610,CT总量表的Cronbach α是0.836。虽然创造力因子的Cronbach α低于0.70,但其他因子以及CT总量表的Cronbach α均高于0.70,这说明中文版本CT量表的五个因子的内部一致性可以接受。
2.重测信度
重测信度又称再测信度,为常用信度评估方法之一。本研究采用重测法对中文版本CT量表的稳定性进行了测量。在被试中随机抽取了36位学生,在这些被试完成第一次调查两周以后,我们对这36名学生又进行了一次测量。研究使用SPSS21.0对这36位同学的前后两次CT测量分数进行相关性分析,从而对CT量表的稳定性进行测量,结果如表3所示。
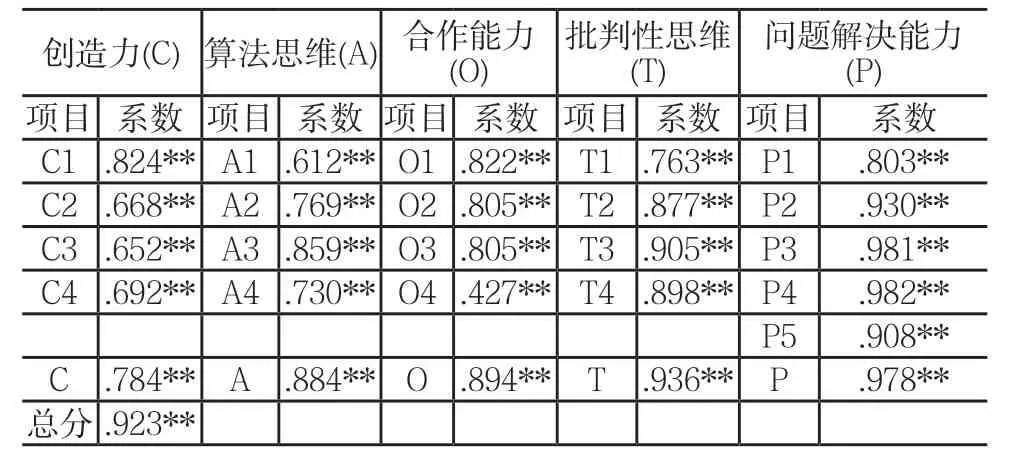
表3 重测结果
从表3可知,通过重测信度的方式得到的各测量指标前后测的相关系数在0.427 - 0.982之间,并且各个测量指标前后相关系数均存在显著正相关。其次,五个因子前后测的相关系数在0.784 - 0.978之间,前后总分之间的相关系数为0.923,各相关系数均存在显著正相关。这说明中文版的CT量表具有良好的稳定性。
(六)K12阶段学生计算思维总体现状及差异分析
1.K12阶段学生计算思维总体现状分析
为了了解我国中学生计算思维的现状,我们对学生在计算思维及其各个维度上的得分均值、标准差、最小值、最大值进行了分析,分析结果如表4所示。

表4 K12阶段学生计算思维总体现状
如表4所示,学生计算思维能力水平最低得分为31分,最高得分为100分,均值为71.6分。68.3%的学生的计算思维水平处于高水平,30.6%的学生的计算思维处于中等水平,只有1.1%的学生的计算思维处于低水平。可见,我国中学生计算思维水平整体较高。就计算思维的每个维度而言,学生的得分均值从高到低依次为:创造力(77.3)、合作(75.2)、批判性思维(73.6)、算法思维(67.5)、问题解决(67.1),即在创造力上得分的均值最高,在问题解决上得分的均值最低。另外,创造力上得分中,处于高水平的人占75.1%。可见,我国K12阶段学生计算思维水平各维度中,创造力水平最高,问题解决和算法思维相对较低。
2.K12阶段学生计算思维差异分析
我们首先对样本数据进行方差齐性检验,方差齐性检验的显著性均达到显著水平,这说明数据适合做单因素方差分析。本研究采用LSD法进行事后多重比较分析。在此基础上,就学生对计算思维的感知水平在性别以及年级上的群体差异进行了单因素ANOVA分析,分析结果如表5、表6所示。从表5可见,学生的计算思维水平在性别上存在显著性差异。总体上,男生的计算思维水平显著高于女生。对于计算思维的各个维度而言,除问题解决之外,在其他维度上,男生得分均高于女生。

表5 不同性别学生计算思维的群体差异分析

表6 不同年级学生对于计算思维的感知水平的群体差异
从上页表6可知,总体上,不同年级学生的计算思维得分存在显著差异,高一年级学生显著高于高二年级。进一步分析发现,对于计算思维的不同维度而言,高一年级学生在批判性思维和问题解决两个维度上的得分均高于高二年级学生,并且存在显著差异,而其他维度上均不存在显著差异。
五、讨论与分析
(一)中文版计算思维量表具有清晰的因子结构
首次探索性因子分析结果显示“问题解决”因子的一个测量指标“合作学习让我感到厌烦”出现交叉载荷,这一测量指标在“问题解决”因子上的因子负荷为0.419,在合作学习上的因子负荷为0.622。其余各因子的测量指标的因子负荷值均大于0.3,且未出现交叉负荷的现象。研究认为造成这一结果可能的原因有两方面。一是中国学生不擅长以合作学习的方式来解决问题[25],因此部分学生在读到这一测量指标的时候会认为这更多的是和合作学习有关,而不是和问题解决相关。二是本研究认为该测量指标的表述本身可能存在问题,建议研究者在使用该量表的时候可以将其修改为“以合作学习的方式来解决问题让我感到厌烦”。鉴于此,研究将删除该测量指标之后的21个测量指标的数据样本进行了第二次探索性因子分析,最终提取出了5个因子。其中,创造力4个测量指标(C1-C4),算法思维4个测量指标(A1-A4),合作能力4个测量指标(O1-O4),批判性思维4个测量指标(T1-T4),问题解决5个测量指标(P1-P5)。
接着,研究对第二批样本数据(n=528)进行了验证性因子分析,采用结构方程模型法确定研究样本数据和中文版计算思维量表五因子结构模型的拟合程度。首先,以χ2/df为标准检验假设模型的拟合效果。当χ2/df<3时,表明模型的拟合效果良好。χ2/df越小,说明模型拟合效果越好。本研究中χ2/df为2.463,这说明中文版计算思维量表五因子的结构模型与数据拟合较好。由于卡方检验对于样本量比较敏感,因此本研究选用GFI这一常用的对样本量不敏感的绝对拟合指标来进一步检测了整个模型可以解释样本方差-协方差的程度。当GFI>0.9时,说明模型拟合度优异。本研究中,GFI为0.905。常用的相对拟合效果检验有NFI、TLI和 IFI。本研究选用NFI,NFI是检测研究模型与拟合最糟糕的独立模型相比较的改善情况,取值范围在0-1之间,当研究模型与理论暗含的模型相差较少时,NFI接近1,反之接近0。一般以0.9作为临界值。在本研究中,NFI为0.92。常见的替代性指标为 RMSEA和CFI。其中,比较拟合指数CFI表示相对于基线模型(变量间不相关的独立模型)研究模型的改善程度,它综合考虑了相对拟合效果和替代性拟合效果。CFI取值范围在0-1之间,越接近1,表明模型拟合效果越好。本研究中,CFI为0.95。其次,RMSEA小于0.01表明假设模型拟合的非常好,小于0.05,表示假设模型拟合的比较好,小于0.1表示假设模式拟合程度可以接受[26]。本研究中,RMSEA为0.053。综上,各拟合指标均达到理想标准,这说明中文版计算思维量表五因子结构模型与研究样本数据拟合效果较好。
(二)中文版计算思维量表具有良好的结构效度与信度
中文版本CT量表的21个测量指标的标准化因子负荷值分布在0.42-0.82之间(均大于0.3),并且五个因子的组合信度值分布在0.58-0.80之间,这表明该CT测量量表具有良好的聚敛效度。其次,中文版计算思维量表五个因子的受限模型与未受限模型相互之间的卡方值差异量均在0.05上达到显著水平,说明该量表具有良好的区分效度。
中文版计算思维总量表的克伦巴赫系数为0.86,在其五个因子中,除创造力之外,其余四个因子的克伦巴赫值皆大于0.7,这说明中文版计算思维量表具有良好的内部一致性。除此之外,研究采用重测法对中文版本CT量表的稳定性进行了测量。重测信度检验表明中文版的CT量表具有良好的稳定性。
综述,本研究认为该CT测量量表可以用于评估中国K12阶段学生的计算思维水平。
(三)中文版计算思维量表的进一步改进
在最后形成的中文版计算思维量表中,所有测量指标的标准化因子负荷值皆大于0.3,达到了可接受水平,但是有些测量指标的标准化因子负荷值还是偏低。本研究认为,首先,这可能与我国传统教育有关:传统的教育大多数都是“填鸭式”,缺乏旨在培养学生问题解决能力、合作能力以及批判性思维的探究式学习、基于问题的学习、项目式学习等新型教学模式。在平时的学习中,学生很少有机会参与到多样化的学习活动中。因此,学生对量表中的有些题目中表述的情境可能都还没体验过,例如“在合作学习中,我喜欢和好朋友一起解决与小组项目有关的问题”中提到“小组项目”,如果学生没有参与过或者很少参与基于项目的合作学习,可能就会感到迷惑,从而影响对题目内涵的理解和判断。又如“我不能逐步应用我所设计的问题解决方案”,如果学生没有参与过任何自己设计问题解决方案并执行方案解决问题的经历,对这一测量指标的表述就难易把握。其次,题目表述的用词可能会影响学生对于其表述内容的内涵的判断。例如,“算法思维”一因子中的“我可以把一个用语言表达的数学问题转化成数学模型”一指标中的“模型”就比较抽象、宏观,影响学生对于题目内容的解读。又如C3中的“直觉判断”,T1中的“解决复杂问题的计划”,T3中的“挑战性的事物”以及P3中的“问题解决方案”都不够具体,这可能会导致学生对其内容理解的差异。鉴于此,建议在对该计算思维量表的后续应用和研究中,有必要对这些题目做一些修改,以进一步提高测量题目的质量。
(四)K12阶段学生计算思维水平总体现状
与美国、英国等发达国家相比较,我国对K12阶段学生计算思维能力培养的重视起步比较晚,2017 新版《普通高中信息技术课程标准》刚刚将其纳入到信息技术课程标准,才逐步开始在具体的课程教学实践中落实。旨在培养学生计算思维的STEAM教育[27]在我国也才刚刚起步,即便如此,从本研究的分析结果来看,我国K12阶段学生计算思维总体上水平并不低,这为我国基础教育领域创客教育、STEAM教育的发展奠定了基础。
对于计算思维的每个维度而言,学生在创造力上的得分最高,合作能力、批判性思维能力次之,而算法思维和问题解决能力得分相对较低。我国中小学教育注重文化知识的学习,学生问题解决能力没有得到足够的锻炼,这使得学生解决问题的能力普遍比较弱。而算法思维强调的是解决问题的一种策略,使得解决问题的过程具有逻辑性,算法思维和问题解决能力相辅相成,互相影响,因此其中一种能力的水平直接影响另外一种。该研究结论给我们的启示是:对于学生计算思维的培养,需要注重对于学生算法思维和问题解决能力的培养。让学生通过解决现实生活中的复杂问题,提高算法思维和问题解决能力。男生的计算思维水平高于女生,这与Korkmaz等人的研究结论相一致。就计算思维的各个维度而言,除问题解决能力之外,在其他维度上,男生都高于女生。这一方面说明女生可能对于自己这些方面的能力不够自信或者女性可能确实在这些方面没有优势。这一研究结论给我们的启示是:在计算思维培养的过程中,应该注重对于女生的关注,给予她们更多的支持,鼓励她们参与相关课程学习,尤其是对于女生创造力、合作能力、批判性思维以及算法思维的培养应该引起重视。
高一年级学生计算思维能力总分均高于高二年级学生,主要是问题解决能力和批判性思维能力高于高二年级,这与Korkmaz等人的研究结论相似。Korkmaz等人的研究发现研究生的计算思维能力随着年级水平的提高而下降,即学生年级越高,计算思维能力水平反而越低。这一分析结果说明传统的学校教育对于学生计算思维的发展似乎没有促进作用。这可能因为在主流的传统教育中,学生大多数时候都是被动的接受知识,对于知识、信息缺乏批判性的思考,这导致学生的批判性思维能力的发展受到了限制。另外,传统教育注重学生知识的记忆和掌握,对于学生问题解决能力的培养有限。学校教育是培养学生能力的重要途径,只有在学校正规教育中获得相应的技能,学生才有可能将其迁移到其他复杂情境中以解决实际生活中遇到的问题。教育实践者应该在教学中,注重学生问题解决能力和批判性思维能力的培养,力争随着学生年级的升高,其问题解决能力和批判性思维能力会有所提高而不是下降。为学生提供各种参与问题解决的机会、情境和过程,引导学生对于所面临的问题提出不同解决方案,通过批判性的分析,找到解决问题的最佳方案,解决问题,从而批判性思维能力和问题解决能力,进一步发展计算思维能力。
六、结语
本研究对Korkmaz等人开发的用于测量K12阶段学生计算思维的量表的因子结构进行了验证,并对该测量量表的聚敛效度、区分效度、内部一致性以及重测信度进行了检验。研究结果表明该量表具有良好的信效度,中文版的计算思维量表的内部一致性及可靠性得到了验证,适合用于测量我国中学生的计算思维能力。因此,本研究为我国研究者和实践者对于K12阶段学生计算思维的评价提供了一个测量工具。
本研究还存在一些不足。仅验证了计算思维量表的五个因子结构,但是对因子之间的相互影响关系没有进一步分析。后续研究将在此基础上,通过对CT量表的5因子结构模型的检验,探讨其五个因子之间的相互预测作用,为实践者和研究者设计与开发培养学生计算思维的课程、主题内容、教学活动等提供依据,为评价学生的计算思维能力水平提供评判工具。另外,研究者可以选择不同的被试,例如以初中生人群为研究对象,进一步探究该量表在中国教育文化背景下的初中阶段的适用性。
