带有标准发生率和信息干预的时滞SIRS传染病模型的稳定性分析
2019-10-16赵英英胡华
赵英英,胡华
( 宁夏大学数学统计学院,宁夏 银川750021)
1.引言
长期以来,人类健康受到传染病的巨大威胁.为了减缓其对人类威胁,大量的数学模型被建立且用于分析传染病的动力学行为.其中经典的是Kermack和Mckendrick[1]对伦敦的黑死病和孟买的瘟疫传播规律的研究.除此以外关于传染病的研究还有许多著名的模型[1−3],这些模型为我们提供了有用的控制措施.一个由Lahrouz 等人提出的SIRS模型[4]有以下形式:

为了更好地控制传染病的传播,除了采取药物管制措施(如接种疫苗和抗病毒药物)以外,还应采取非药物控制措施(包括信息干预)[5−6].在传染病传播初期,由于药物干预措施的缺乏有必要研究一个由于非药物控制措施即信息干预对疾病流行影响的模型.Kumar[6]等人提出了连续SIRS传染病模型:
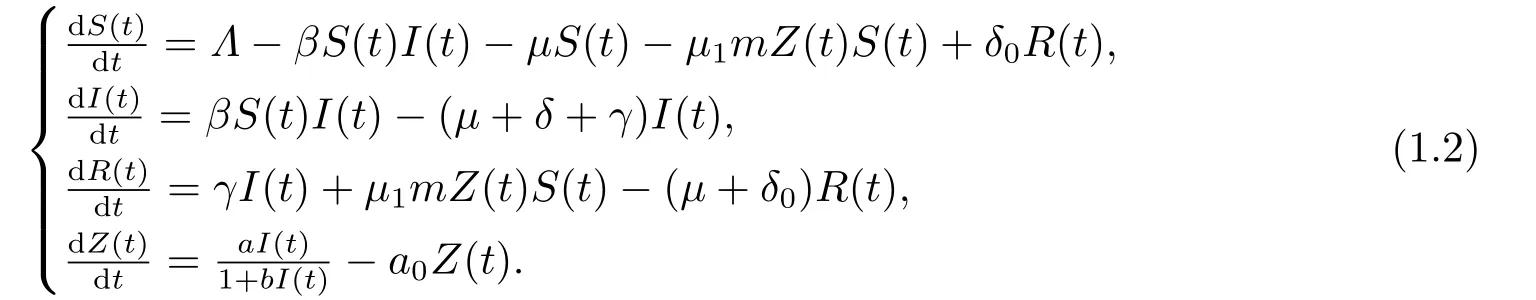
上述两个模型均没有考虑时滞的影响,这是不符合实际的.事实上,流行病的传播具有时滞这一特点具体包括潜伏期时滞,感染期时滞,失去免疫期时滞等[7−9].Cooke[10]研究了一个带时滞的SIR模型,其中传染率函数为βS(t)I(t−τ),τ是一个固定时间,只有经过这段时间,易感人群才能被感染者感染.模型如下:

结合这三个模型,即考虑时滞影响及标准发生率下的SIRS模型:
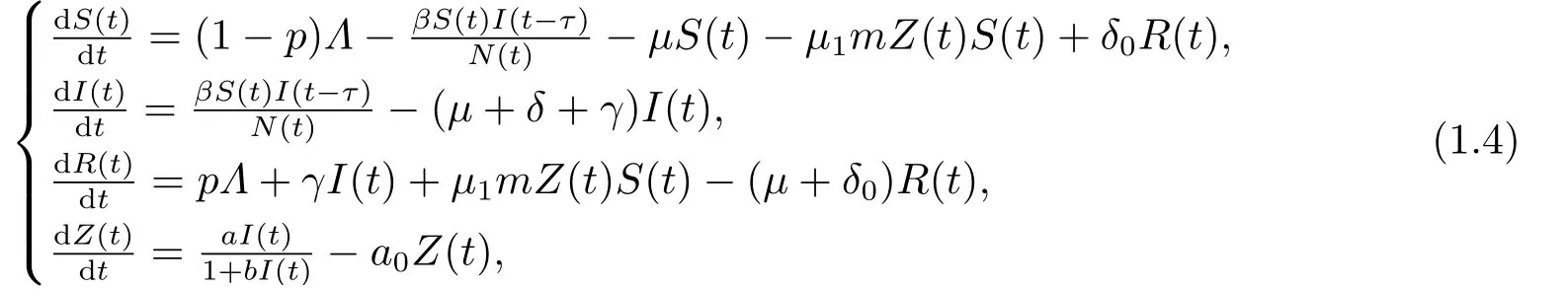
其中S(t),I(t),R(t)和Z(t)分别代表易感人群,感染人群,恢复人群和信息在t的数量,I(t−τ)代表在t时刻经过潜伏期后处于感染期的感染者数量,τ >0是一定值,代表已感染者成为带菌者所需要的时间,N(t)=S(t)+I(t)+R(t).Λ是人口的流入率或更新率,其中比例p的人是接种疫苗的,1−p是容易感染的(0≤p≤1).γ是感染人群的恢复率,µ是自然死亡率,δ是疾病引起的死亡率,β是接触传播系数,δ0(=δ1+δ2)表示失去免疫的总比率,包括失去自然免疫的比率δ1和失去由于保障措施所得的免疫力的比率δ2,m表示信息交互率,µ1(0≤µ1≤1)代表反应强度,a表示信息的增长速度,b是饱和常数,a0是信息的自然衰减率.所有参数假定非负.
基本再生数[11]是流行病学中的一个重要概念.模型(1.4)的基本再生数为

模型(1.4)有两个均衡点[6]:一个是无病平衡点另一个是地方病平衡点E∗=(S∗,I∗,R∗,Z∗).无病平衡点总是存在的,地方病平衡点只有满足R0>1才存在.
2.平衡点的局部渐近稳定性分析
本节通过分析模型(1.4)对应的特征方程,分别对模型(1.4)的无病平衡点和地方病平衡点E∗=(S∗,I∗,R∗,Z∗)的局部渐近稳定性进行讨论.
引理2.1(Routh-Hurwitz 判据)[12]设给定常系数的n次代数方程
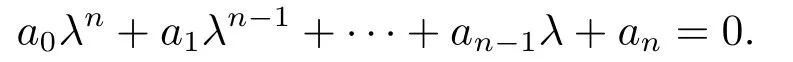
该方程的所有根具有负实部的充要条件是下述所有行列式同号
构造上述行列式时,若i>n,则取ai=0.
定理2.1τ≥0时,若R0<1,则模型(1.4)在无病平衡点处是局部渐近稳定的;若R0>1,则模型(1.4)在E0处不稳定.
证模型(1.4)在无病平衡点处的Jacobian 矩阵是

从而在E0处的特征方程为

不难发现(2.1)有三个特征根λ1=−µ<0,λ2=−(µ+δ0)<0,λ3=−a0<0,为求(2.1)的另一个根,令
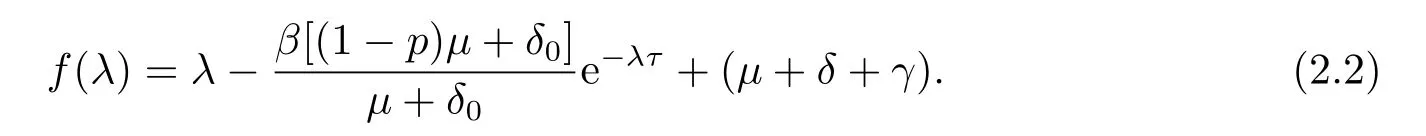
当τ=0时,(2.2)化为f(λ)=λ+(µ+δ+γ)(1−R0),该方程的根λ4=(µ+δ+γ)(R0−1).当R0<1时,特征方程的四个根均小于0,故该模型的无病平衡点E0是局部渐近稳定的.反之,当R0>1时,λ4>0,所以E0不稳定.
当τ >0时,f(λ)表达式仍为(2.2).设f(λ)=0的根为λ=α+iβ,将其代入f(λ)中得

比较实部和虚部得到

当R0<1时,此时,特征方程(2.1)的所有根的实部均为负,所以E0局部渐近稳定.当R0>1时,有
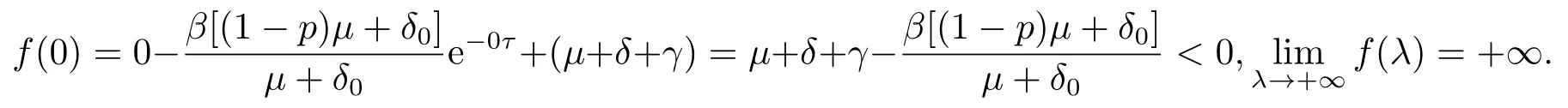
此时,f(λ)=0有一个正实根.所以当R0>1时,E0不稳定.
注当R0<1时,对任意的τ,模型(1.4)在无病平衡点处局部渐近稳定;当R0>1时,对任意的τ,模型(1.4)在无病平衡点处不稳定,即R0是模型(1.4)的一个阈值.
定理2.2假设R0>1成立且τ=0时,模型(1.4)的地方病平衡点E∗局部渐近稳定.
证模型(1.4)在地方病平衡点E∗=(S∗,I∗,R∗,Z∗)处的Jacobian矩阵是

从而在E∗处的特征方程为
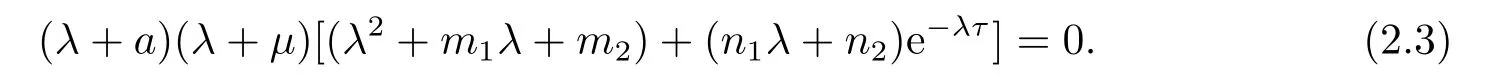
不难发现,(2.3)有两个特征根λ1=−a<0,λ2=−µ<0,令
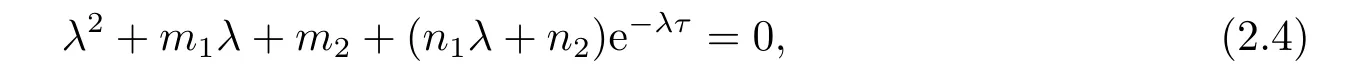
其中
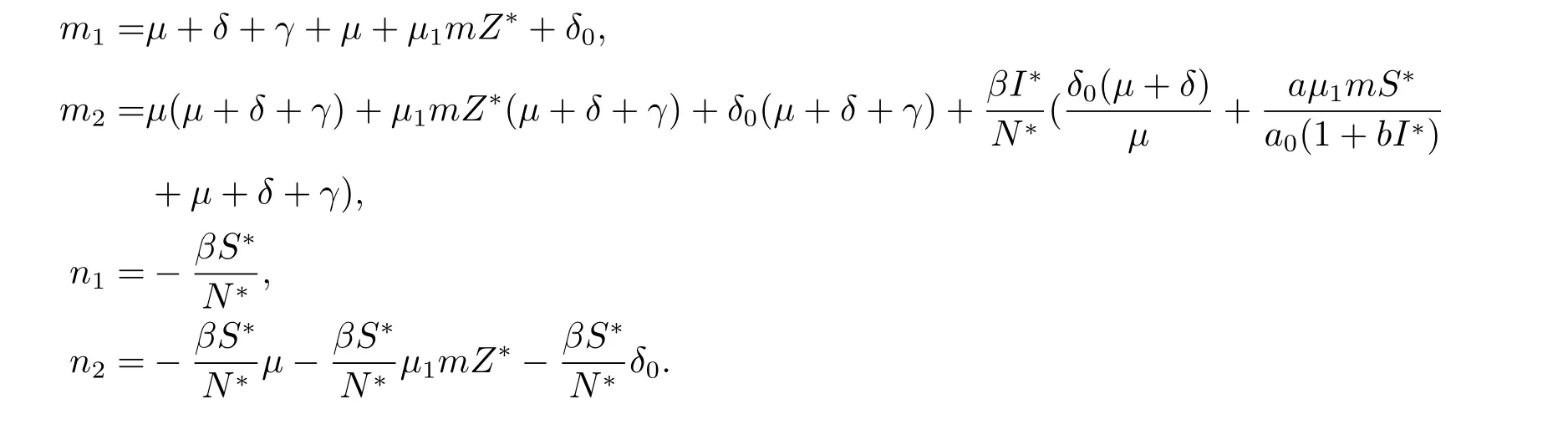
当τ=0时,(2.4)式化为λ2+(m1+n1)λ+m2+n2=0.则
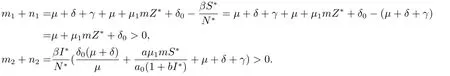
根据Routh-Hurwitz判据可得当τ=0时,(2.4)式有两个负实根.所以此时特征方程的所有根都是负实根,定理得证.
定理2.3假设R0>1成立且τ >0时,若(µ+µ1mZ∗+δ0)2−µ+δ+γ)>0,则模型(1.4)的地方病平衡点E∗局部渐近稳定.
证用反证法证明上述结论.假设方程(2.4)有非负实部,则其解必须是虚数.由τ=0到τ >0的过程中,必有一个τ∗>0,使得(2.4)有纯虚根.不妨设λ=iw是(2.4)的解.代入得

整理上式可得
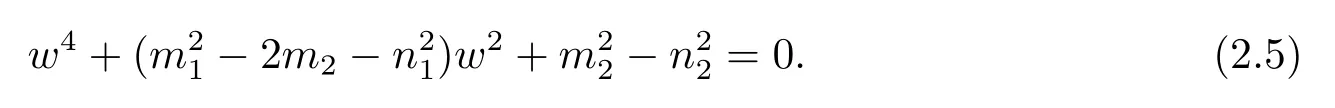
令u=w2,(2.5)式化为

则

根据Routh-Hurwitz判据可得(2.6)式无正实根.即u=w2无根,即不存在纯虚根λ=iw,也就是E∗的稳定性不变,故R0>1且τ >0 时,若(µ+µ1mZ∗+δ0)2−+µ+δ+γ)>0,E∗局部渐近稳定.
3.平衡点的全局渐近稳定性分析
引理3.1(Halanay不等式)[13]设f(t)≥0且连续(t≥t0−r),0<β <α,f′(t)≤−αf(t)+β ‖ft ‖,t≥t0,‖ft ‖=supt−r≤s≤t | f(s)|,则f(t)≤‖ft0‖e−λ(t−t0)(t≥t0),其中λ=α−βeλr.
定理3.1若β <µ+δ+γ且1,则模型(1.4)的无病平衡点E0是全局渐近稳定的.
证任取模型(1.4)满足初始条件的正解(S(t),I(t),R(t),Z(t)),若β <µ+δ+γ,1,取任意小的ϵ>0,使其满足:

将模型(1.4)的前三个方程相加,可知人口总量N(t)=S(t)+I(t)+R(t)满足如下微分方程:
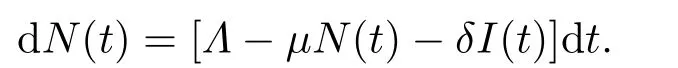
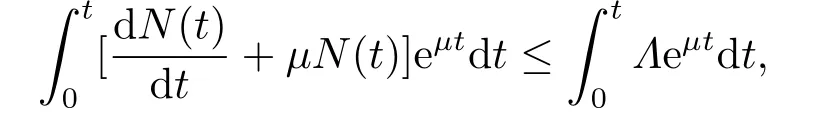
因此有:
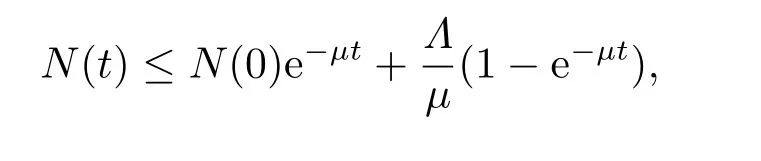
进一步可以得到:

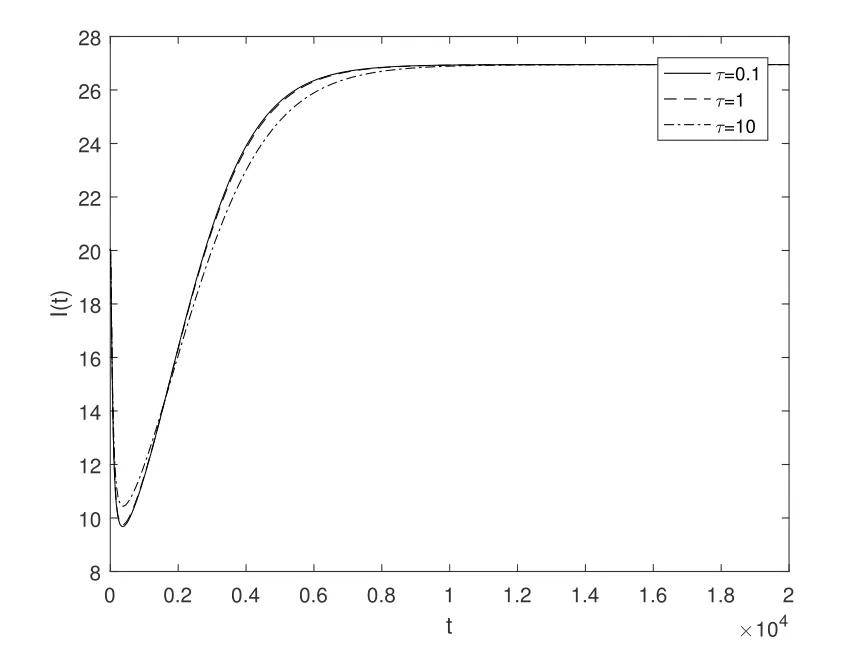
因此模型的所有解S,I,R均具有上界设所以对于满足(3.1)的足够小的ϵ>0,存在T1>0,使得当t>T1时,有S(t) 对上述ϵ>0,当t>T1+τ时,由模型(1.4)的第二个方程有: 由引理3.1 和(3.1)有所以对于满足不等式(3.1)的足够小的ϵ>0,存在T2>T1+τ,使得当t>T2时,有I(t)<ϵ成立. 对上述ϵ>0,当t>T2时,由模型的最后一个方程有: 经计算得 令ϵ→0,我们有另一方面,因此所以对满足不等式(3.1)的足够小的ϵ>0,存在T3>T2,使得当t>T3时,有Z(t)<ϵ成立. 对上述ϵ>0,当t>T3时,由模型的第三个方程有: 经计算有 令ϵ→0,我们有 另一方面 经计算有 由不等式(3.2)和(3.3),我们有 所以,对任意ϵ>0,存在T4>T3,使得当t>T4时,由模型的第一个方程有: 经计算有 令ϵ→0,我们有 另一方面 令ϵ→0,我们有 由不等式(3.4)和(3.5),我们有 综上,若β <µ+δ+γ且<1,模型(1.4)的无病平衡点E0是全局渐近稳定的. 定理3.2若R0>1,sgn(S(t)−S∗(t))=sgn(I(t)−I∗(t))=sgn(R(t)−R∗(t))=sgn(Z(t)−Z∗(t)),则模型(1.4)的地方病平衡点E∗是全局渐近稳定的. 证令x=S−S∗,y=I−I∗,u=R−R∗,v=Z−Z∗.构造Lyapunov函数 则 其中ϱ=min{µ,a0}.将上式两边从0到t积分得 因此,对任意t≥0,V(t)在[0,t]内有界同时 故 定理得证. 注当β <µ+δ+γ且<1时,模型(1.4)的无病平衡点E0是全局稳定的,这表明在此条件下该传染病将逐渐消失不会流行;当R0>1时,模型(1.4)的地方病平衡点E∗是全局稳定的,这表明在此条件下该传染病将会流行并将最终成为地方病. 继研究带有标准发生率和信息干预的时滞SIRS传染病模型平衡点的局部渐近稳定性和全局渐近稳定性之后,下面对该模型进行可视化并借助Matlab 7.1来进一步分析信息干扰因素以及系统一些参数对疾病传播的动力学影响.对模型(1.4),令参数的取值为: 方程的初始值为(S0,I0,R0,Z0)=(479.0,20.0,1.0,10.0). 例4.1可变参数µ1的作用 下面研究人们对信息的反应强度(以下简称“反应强度”)µ1的作用.式(4.1)中取β=0.02,τ=0.1,其余参数不变,此时R0>1.图4.1给出反应强度µ1取不同值(µ1=0.00,0.25,0.50,0.75,1.00)时,模型(1.4)中I(t)的时间序列图.从图可以看出,在患病人数趋于稳定时,信息干预可以减少患病人数. 图4.1 反应强度µ1对I(t)的影响 例4.2可变参数β的作用 下面研究接触传播系数β的作用.式(4.1)中取µ1=0.25,τ=0.1,其余参数不变,此时R0>1.图4.2,图4.3分别给出接触传播系数β取不同值(β=0.02,0.2)时,模型(1.4)中对应的S(t),I(t)的时间序列图.图4.2(b)和图4.3(b)分别为对应的图4.2(a)和图4.3(a)的局部小图.从图4.2可以看出在初始阶段S(t)的变化较为复杂,之后S(t)趋于稳定且此时β越大,易感人数越少.从图4.3可以看出在初始阶段I(t)的变化较为复杂,之后I(t)趋于稳定且此时β越大,感染人数越多. 图4.2 接触传播系数β对S(t)的影响 例4.3可变参数τ的作用 下面研究时滞τ的作用.式(4.1)中取µ1=0.25,β=0.02,其余参数不变,此时R0>1.图4.4,图4.5分别给出时滞τ取不同值(τ=0.1,1,10 ) 时,模型(1.4)中对应的S(t),I(t)的时间序列图.从图4.4,图4.5可以看出,在初始阶段不同的时滞τ对S(t),I(t) 产生不同的较为复杂的变化,之后S(t),I(t)均趋于稳定且与时滞无关,即经过一段时间后模型(1.4)的地方病平衡点E∗全局稳定且与时滞无关. 图4.3 接触传播系数β对I(t)的影响 图4.4 τ对S(t)的影响 图4.5 τ对I(t)的影响 总之,本文研究了一类带有标准发生率和信息干预的时滞SIRS传染病模型.通过分析模型的特征方程,讨论了无病平衡点和地方病平衡点局部渐近稳定性.应用Halanay不等式对无病平衡点的全局渐近稳定性进行了证明.通过构造适当的Lyapunov函数讨论了地方病平衡点全局渐近稳定性.最后运用Matlab 7.1进一步分析了信息干扰因素以及系统一些参数对疾病传播的动力学影响.


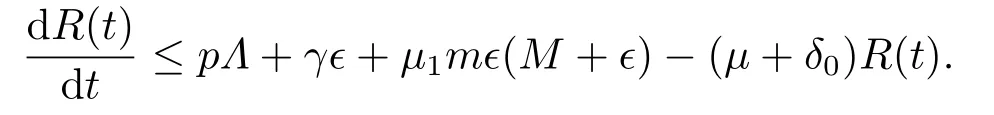
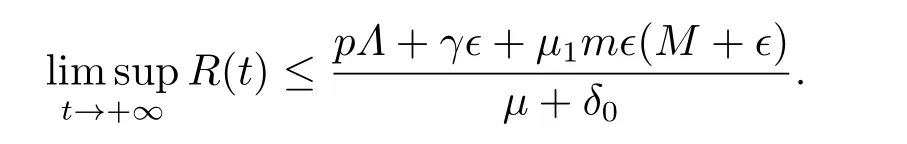

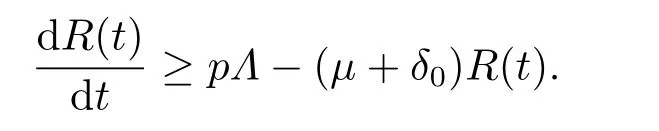


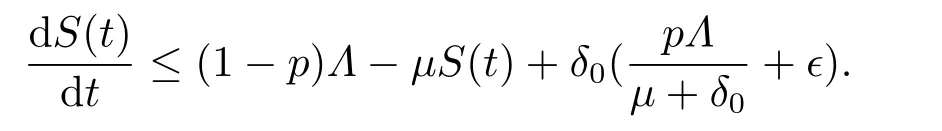

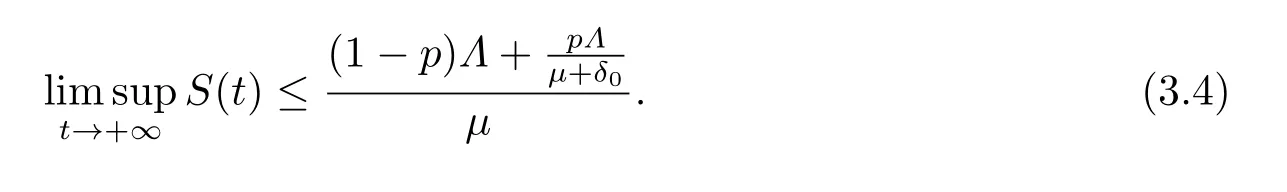

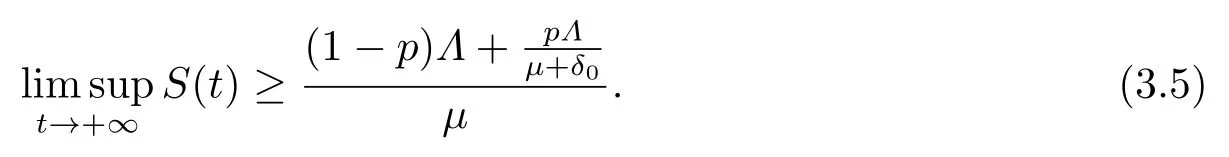




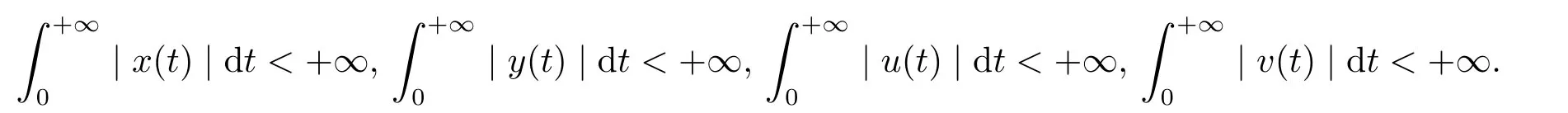

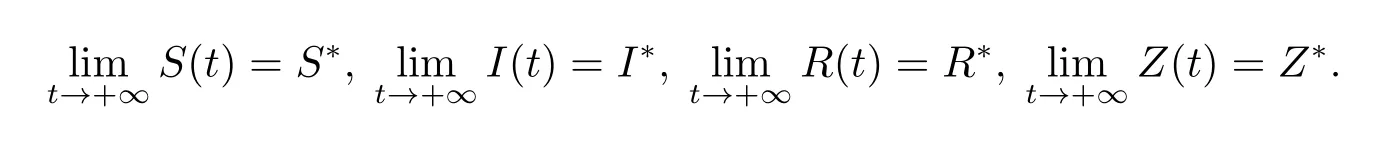
4.数值分析和结论
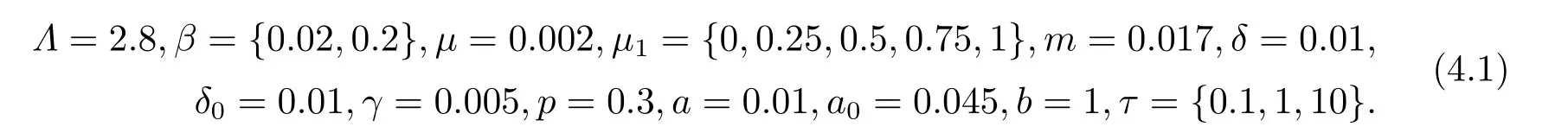




猜你喜欢
杂志排行
应用数学的其它文章
- 凸二次半定规划一个新的原始对偶路径跟踪算法
- Numerical Solution of Nonlinear Stochastic Itô-Volterra Integral Equations by Block Pulse Functions
- 面板数据分位数回归模型的工具变量估计
- Stability Analysis of Indirect Adaptive Tracking Systems for Simple Linear Plants with Unknown Control Direction
- The Boundedness of Maximal Dyadic Derivative Operator on Dyadic Martingale Hardy Space with Variable Exponents
- Positive Solutions for Kirchhoff-Type Equations with an Asymptotically Nonlinearity
