指针式仪表数值识别方法

王 涛，刘思邦

(周口师范学院 物理与电信工程学院，河南 周口 466001)

指针仪表由于结构简单、价格便宜、抗干扰能力强，并且具有防尘、防水、防冻等优点，至今被广泛使用在工业仪器仪表领域中，而其数值识别一直是业界研究的热点[1-3]. 传统的仪表数值主要依靠人工肉眼识别，但由于受仪表数量较多、所处外界环境复杂等因素的影响，人工识别过程枯燥琐碎并且容易受主观因素影响，不可避免地会造成读数不精确，同时在危险场合下更是无法采用人工进行读数. 随着数字图像处理技术和电子技术的发展，摄像头代替人对仪表数值识别已经成为趋势[4-5]，越来越受到业界学者的重视，近年来国内外学者对此进行了大量的研究，取得了一系列成果.

国内外学者对仪表数值识别的研究，目前主要集中在采用基于Hough变换的指针定位提取与识别，但是由于外界复杂环境以及指针仪表本身的影响，使得仅使用基于Hough变换的识别算法，具有一定的局限性. 倪刚等[6]提出了一种以表盘半径和指针的旋转中心作为先验特征的指针定位算法，该算法基于Canny边缘算子和Hough直线检测算法，但是文中计算指针角度的公式采用估计法，误差较大. 魏琦等[7]结合数字图像处理和人工神经网络等技术，对指针式仪表示值的自动判读方法进行了研究，但是没有考虑到图像倾斜导致指针读数不准确的问题. 施健等[8]先使用图像减影法大致得到指针轮廓，接着通过处理对指针图像进行细化，最后利用Hough变换得到指针夹角. 刘玉翠等[9]首先用Retinex算法对待测图像进行增强处理，然后对增强后的图像进行阈值处理、Hough变换进而提取到指针，最后用查表法读取仪表示数，但是需要事先计算出指针刻度值和角度之间的一一对应关系，该方法计算数据量大，要求较高. 滕今朝等[10]用双阈值Hough变换算法，但是仅把位置在指针角度范围的像素点进行变换，这种方法误差较大. 李祖贺等[11]提出了用帧差分法和角度法来自动识别指针仪表读数，同时提出利用区域极值点确定指针质心来解决残缺指针区域的质心偏移问题，但是没有考虑指针宽度对指针读数的影响.

基于以上分析，针对目前指针仪表数值识别方法存在的一些不足和缺陷，本文以某型号压力表为例，提出了一种指针仪表数值识别方法，图1是使用彩色CCD摄像头获取该压力表的待测图像，该方法首先对待测图像进行预处理，然后使用Retinex增强算法解决外界光照、雾气等因素对仪表数值的影响；接着提出图像矫正算法，用于将倾斜的待测图像矫正为标准图像，便于对其数值进行识别；最后用像素投影法和基于Hough变换的旋转投影法来识别表盘指针的方向及角度，提高了指针角度识别的速度和精度.该方法不仅保留了目前已有仪表表盘识别算法简单、精度高和易于实现的优点，而且可以有效地解决待测图像倾斜、不均匀光照、环境雾气等因素对数值识别带来的影响.

图1 压力表的待测图像

1 仪表数值识别算法流程

本文提出的仪表数值识别流程包括5个部分：图像预处理、图像矫正、图像再处理、指针角度及方向检测、计算仪表数值.

1.1 图像预处理

1.1.1 灰度化

由于待测图像是彩色图像，需要首先将其转化成灰度图像，本文选择加权平均法来进行图像灰度化处理，加权平均法是将彩色图像中每个像素F(x,y)的三个原色光谱分量(红色：F(x,y)R、绿色：F(x,y)G、蓝色：F(x,y)B)以不同的权值进行加权平均，然后将得到的像素值作为对应灰度图像在该位置的灰度值G(x,y)，其计算方法如式(1)所示：

G(x,y)=0.029 9F(x,y)R+0.587F(x,y)G+0.114F(x,y)B

(1)

灰度化后的图像如图2所示：

图2 灰度图像

1.1.2 中值滤波

压力表可能会受到外界环境因素的影响，使得待测图像存在噪声，本文采用中值滤波滤除图像噪声，本文选用3×3窗口大小掩膜的中值滤波对待测图像进行滤波[12].

中值滤波后的图像如图3所示：

图3 中值滤波图像

1.1.3 图像增强

压力表所处的环境大都恶劣、复杂，外界环境因素会对其数值识别造成影响，例如：外界光照强弱不同、环境雾气的影响等，本文采用基于Retinex的增强算法对图像进行增强处理，使处理后的待测图像在保留原图像细节的基础上，尽可能的消除噪声. Retinex理论认为原始图像S(x,y)是由反射图像R(x,y)和亮度图像L(x,y)所构成，即三者满足以下等式[13]：

S(x,y)=R(x,y)*L(x,y)

(2)

则可以通过消除亮度图像L(x,y)的影响，进而从原始图像S(x,y)中得到更真实的反射图像R(x,y)，但是目前对亮度图像L(x,y)还没有一个确切的定义，只能进行估计，本文采用单尺度的Retinex增强算法来对待测图像进行增强处理，处理流程如下：

1)对式(2)两边取对数，分离出反射图像R(x,y)和亮度图像L(x,y)：

logS(x,y)=logR(x,y)+logL(x,y)

(3)

2)使用高斯低通滤波器G(x,y)对原始图像S(x,y)进行低通滤波，得到滤波平滑后的图像D(x,y)：

(4)

D(x,y)=S(x,y)*G(x,y)

(5)

其中：*是卷积算子

3)在对数域中，用原图像S(x,y)减去低通滤波后的图像D(x,y)，得到高频增强的图像F(x,y)：

F(x,y)=logS(x,y)-logD(x,y)

(6)

4)对高频增强图像F(x,y)取反对数，得到增强后的反射图像R(x,y)，即为增强后的图像：

R(x,y)=eF(x,y)

(7)

1.2 图像矫正

由于摄像机、仪表在安装、制造中可能会出现误差，导致待测图像出现倾斜，会影响数值识别，因此需要事先对倾斜的待测图像进行矫正，使其变为标准图像. 图像矫正是指按照给定模板图像的尺寸、角度等属性对待矫正图像进行透视变换，本文提出的图像矫正算法流程如下：

图4 增强后图像

步骤1. 提取待测倾斜图像和模板图像的Surf(它是数字图像中一种稳健的局部特征点检测和描述算法)特征，分别得到对应的Surf特征描述子，其中：模板图像是标准的非倾斜图像；

步骤2. 用欧氏距离对得到的两个Surf特征描述子进行匹配，得到匹配的Surf特征描述子点对，匹配的规则：每个Surf特征点对之间的欧氏距离越短，表示这两个特征点越匹配；

步骤3. 选取步骤2得到的已配对Surf特征描述子点对中的前10个特征描述子点对作为最优描述子，根据其坐标计算待测倾斜图像和模板图像对应的变换矩阵；

步骤4. 利用步骤3所得到的变换矩阵对待测倾斜图像进行透视变换，得到矫正后的标准图像.

图5(a)是标准模板图像，图5(b)是待测倾斜图像(为了验证本文提出算法的可靠性，本文假设待测倾斜图像的倾斜角度为90°，实际上一般达不到90°)，使用本文提出的矫正算法对倾斜图像进行矫正，最终结果如图5(c)所示，可以看到其与模板图像几乎一致，说明本文提出的图像矫正算法具有较高的精度，可以实现对待测倾斜图像进行矫正.

(a)模板图

(b)待测倾斜图像

(c) 矫正后图像

图5图像矫正

1.3 图像再处理

1.3.1 图像二值化

本文采用Otsu算法(最大类间方差法)对待测图像进行二值化处理，Otsu能够自适应确定图像的全局最佳阈值，它假定阈值k把待处理图像分成两类，如果此时满足条件：这两类的类内方差值最小并且类间方差值最大，那么该k值就是要找的最佳阈值，此时二值化后的图像可以用以下式子表示[14]：

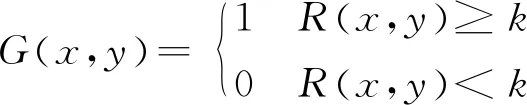
(8)

如果不满足上述条件，那么就继续迭代寻找k值，直至满足这个条件，使用Otsu算法二值化后的待测图像如图6所示：

图6 二值化图像

1.3.2 形态学处理

本文采用腐蚀和膨胀形态学算法对二值化后的待测图像做进一步处理，以突出指针. 腐蚀算法用于增大二值化图像中的黑色目标区域，缩小白色背景区域；膨胀算法用于增大二值化图像中的白色背景区域，缩小黑色目标区域，进而细化指针区域，消除小范围的黑色干扰区域[15]. 本文首先对二值化后的待测图像进行膨胀处理，消除微小区域的黑色噪声区域，然后使用腐蚀算法对膨胀后的待测图像进行处理，进一步突出指针区域，形态学算法处理后的结果如图7所示：

(a)形态学腐蚀后图像

(b)形态学膨胀后图像

图7形态学图像

1.4 指针方向及角度大小确定

1.4.1 指针方向的确定

仪表指针大都具有一定长度、顶端细、底端粗的特征，并且指针轴心两端长度不等，当指针和水平方向平行时，指针在水平方向的投影宽度最大；当指针和水平线垂直时，指针在水平方向的投影宽度最小；当指针处于其他位置时，指针在水平方向的投影宽度介于这二者之间，结合以上特征，本文提出像素投影法来确定指针方向. 像素投影法的流程如下：首先以指针轴心作为坐标原点建立直角坐标系XOY，如图8所示，则当指针与X轴重合的时候，指针像素在X轴上的投影范围最宽，而当指针与Y轴重合的时候，指针像素在X轴上的投影范围最窄，当指针不与X、Y轴重合时，指针像素在X轴上的投影范围介于最宽和最窄之间，同时指针零灰度值像素在X轴方向上的投影规律为：指针顶端部分灰度值为零的像素个数较少，而指针末端部分灰度值为零的个数较多，因此根据以上特征可确定指针的方向.

如果沿着X轴负方向到正方向灰度值为零的像素个数有逐渐减少的趋势，如图8(a)所示，那么此时指针顶端位于Y轴的右侧；如果沿着X轴负方向到正方向灰度值为零的个数有逐渐增加的趋势，如图8(b)所示，那么此时指针顶端位于Y轴的左侧.

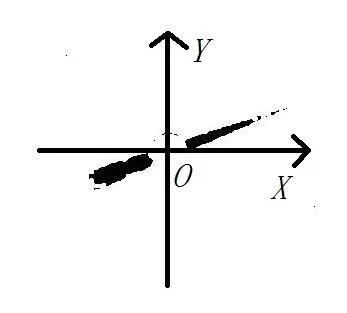
(a)顶端在Y轴右侧

(b)顶端在Y轴左侧

图8指针方向的识别

1.4.2 指针角度的确定

Hough变换是利用图像空间和参数空间之间的关系，在二值图像中寻找直线的一种相对快速算法，它将欧式空间中的直角坐标变换为极坐标空间的坐标. 如果将图像空间看作是欧式空间，则图像空间中处于同一条直线上的像素点越多，那么在极坐标空间中这些点所对应的曲线相交于一点的数量越多，据此可以根据曲线相交于一点的累计量判断图像空间中的某些像素是否在同一条直线上[16].

本文采用基于Hough变换的旋转投影法检测指针角度，处理流程如下：仪表指针的两个边缘分别是两条最长的直线，这两条直线的倾斜角度分别对应待测二值图像中直线的最大角度和最小角度，首先用Hough直线变换检测待测图像中的所有直线，得到所有直线的角度，然后取最大角度和最小角度，记最大角度为：θmax，最小角度为：θmin，令：

θ=(θmin+θmax)/2

(9)

其中：θ为待测图像指针的预估角度.

记待测图像指针的实际角度为：θε，指针从初始位置顺时针或者逆时针旋转到Y轴正方向时所经过的角度为：θδ，则有：

a)θ>0°

①如果由像素投影法确定指针顶端位于Y轴的右侧

以一个固定角度逆时针旋转该指针，直至到达Y轴正方向，即此时指针在X轴投影宽度最小，可得：

θε=θδ+90°

(10)

②如果由像素投影法确定指针顶端位于Y轴的左侧

以一个固定角度顺时针旋转该指针，直至到达Y轴负方向，即此时指针在X轴投影宽度最小，可得：

θε=θδ+270°

(11)

b)θ<0°

①如果由像素投影法确定指针顶端位于Y轴的右侧

以一个固定角度顺时针旋转该指针，直至到达Y轴负方向，即此时指针在X轴投影宽度最小，可得：

θε=θδ+180°

(12)

②如果由像素投影法确定指针顶端位于Y轴的左侧

以一个固定角度顺时针旋转该指针，直至到达Y轴正方向，即此时指针在X轴投影宽度最小，可得：

θε=90°-θδ

(13)

c)θ=0°

指针角度θε为：θ.

其中：为了保证精度，该固定角度可取0.01°；假设指针沿着水平X轴负方向时的角度为0°.

1.5 识别仪表指针数值

由图1中仪表表盘的特征得知，其单位刻度对应的角度为9°，单位刻度对应的数值为0.05 Mpa，可得仪表刻度值λ与指针角度θε的函数关系为：

(14)

式中：λ的单位为Mpa.

2 实验与验证

本文采用Visual Studio 2013、Opencv 2.4.9作为软件开发平台，C++作为开发语言对本文提出的指针式仪表识别方法进行验证，以图1所示的指针压力表为测试对象，获取该压力表的不同数值图像，验证本文算法的可行性.

2.1 仪表指针数值计算实验

根据图8，由本文提出的像素投影法可得待测图像指针顶端方向位于Y轴的左侧，且θ>0°，然后由1.4.2节可确定待测图像指针角度是θδ+270°，通过旋转投影法算法可确定θδ为63.2°，则待测图像指针的角度是333.2°，最后由式(14)可得该待测图像的数值是：0.148 89 Mpa，而通过人工读数得到的数值是0.15 Mpa，两者较为接近，且本文精度更高，证明本文提出的识别算法具有较高的精度和准确性.

2.2 实验测试结果

为了进一步检测算法的适用性和稳定性，本文采集了该压力表5幅不同数值的图像样本，使用本文提出的识别方法对每幅图像进行100次实验，总计500次实验. 表1为最终的测试结果，从表中可以看到本文提出的识别方法与人工读数之间的平均误差为0.001 3 Mpa，两者结果基本接近，说明本文方法具有较好的精度和稳定性.

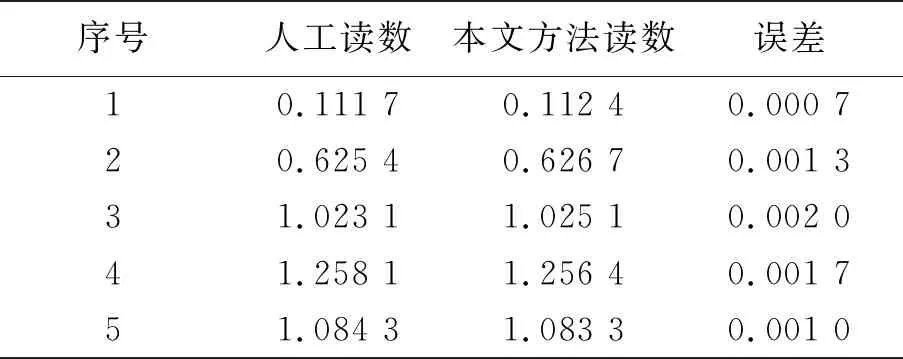
表1 数值识别结果

由于仪表多处于复杂环境中，表盘表面可能会有污渍，同时表盘上大都印有文字等(如图1)，这些因素都可能会对指针数值的识别造成影响. 本实验中所使用的仪表表盘印有生产厂家、仪表型号等文字符号，而由表1的结果可知，本文算法对文字干扰具有较强的适用性，而污渍的影响可以认为等同于文字的影响，因此本文算法对污渍干扰也同样具有较强的稳定性. 摄像机、仪表在安装、制造过程中或摄像机拍摄不标准等因素都可能导致待测图像出现倾斜，本文提出的图像矫正算法可以对待测图像进行矫正，得到标准图像，进而可以消除图像倾斜带来的数值识别误差问题.

3 结论

本文提出了一种指针仪表数值识别方法，可以对复杂环境中仪表的数值进行识别，该方法包括5个步骤：图像预处理、图像矫正、图像再处理、指针角度及方向检测、计算仪表数值，首先通过预处理算法对待测图像进行预处理；提出了图像矫正算法，可对倾斜图像进行矫正，便于正确识别指针数值；然后对待测图像进行再处理得到指针区域；接着根据仪表指针的特征，提出了像素投影法和基于Hough变换的旋转投影法来确定指针方向及角度，接着给出了仪表数值和指针角度之间的函数关系，得到仪表的数值，最后通过大量实验验证表明本文方法与人工读数之间误差较小，并对外界复杂因素的干扰具有较好的稳定性，同时解决了图像倾斜导致的数值识别误差问题，因此本文的仪表指针数值精度和准确度具有较高的优势.