基于二元特征的断面交通数据异常检测与修正*
2019-10-16康晋滔
康晋滔,成 卫,张 灵
(1.昆明理工大学 交通工程学院,云南 昆明 650504; 2.昆明市公安局交警支队科信处,云南 昆明 650000)
0 引言
随着智能交通系统(Intelligent Transportation Systems,ITS)的引入和普及,交管部门已有庞大的交通原始数据积累。这些交通数据在交通控制、交通规划等领域蕴含了极大的潜在价值[1]。然而,受环境因素、设备故障等影响,这些数据的准确性仍有待提高。研究表明,交通数据库里的数据准确率平均值低于70%[2]。因此,为保障智能交通系统有效工作,对其原始数据的异常检测与修正尤为必要。
20世纪90年代,Jacobson等[3]学者通过建立交通数据最值模型,得到经典3参数的阈值基准,从而对异常值进行检测;Zhong等[4-5]在此基础上,采用了插值、回归等方法,对数据进行修正;Min等[6]基于交通数据的时空相关性,利用邻接数据、历史数据等对原始数据进行修正。国内对于此类问题的研究起步较晚,大约在2005年后,姜桂艳等[7-9]针对实时动态的交通数据提出了异常评价体系;徐程等[10]根据前人的研究成果,建立了一套标准的数据预处理流程。但是这些方法,在大数据时代下,难以高效地处理爆炸式增长的交通数据。
随着机器学习和深度学习的普及,部分学者也开始尝试训练模型来处理数据。范光鹏等[11]充分挖掘了数据在时间序列上的信息,利用深度学习LSTM模型与卡尔曼滤波相结合,来预测公交车站到站时间;Sun等[12]在传统的KNN算法基础上,引入时间窗和权重,极大拓展了数据集规模,从而在大数据框架下建立了GSW-KNN算法;Kim等[13]则是采用优化的递归神经网络C-LSTM模型,通过对大量历史交通数据的深度挖掘,训练特定场景的数据模型,来检测该场景下的交通异常值。
综上所述,基于交通数据时空相关性的处理方法,没有充分挖掘数据本身的逻辑规律。然而由于道路条件等诸多随机因素存在,在实际工程中交通数据的变化往往无法呈现出既有模型所具有的规律性,所以基于时空相关性的修正方法可能会出现较大的误差。常用的交通异常检测手段,多基于数据的单元特征,分别对速度或流量等参数进行异常检测,随着数据多元化的发展,已经无法满足智能交通系统的要求。而在数据修正过程中,传统方法大多根据交通数据的时空特性,使用大量的历史数据,通过不同的权重来对异常点进行相应修正。
基于此,提取断面二元特征向量速度与流量,运用多元高斯分布机器学习模型来进行异常数据的快速甄别。同时鉴于灰色马尔可夫模型[14]在短时预测的领域有着优良的拟合效果,提出了1种基于GM(1,1)-Markov模型的异常值修正方法,在此基础上引入了小时修正窗口和波动性数据处理,从便捷性和准确性2方面优化了该组合模型。
1 基于多元高斯分布的异常检测
1.1 原始数据集二元特征向量提取
交通原始数据呈现多源异构特征,为了便于后续的运算处理,首先要对原始数据集进行标准化处理。本文以10 min为基本单元进行标准化,则每天的速度数据和流量速度分别有144组,即V=v1,v2,v3,,v144,Q=q1,q2,q3,,q144。原始数据集最终可表示为Xt=(V,Q),式中t为该数据集的日期,即t=1,2,3,,31。取第1天交通数据X1为训练集,并对X1进行异常标定,用于多元高斯异常检测模型的训练。
1.2 基于速度和流量的二元高斯异常检测
实际工程中,即使数据分布不太符合高斯分布,可以通过函数变换使其满足高斯分布,这一过程称为高斯化。大量的实验[15]表明,原数据不进行高斯化处理,异常检测算法也能够良好运行。因此,本文认为流量、平均速度等数据服从高斯分布。
根据交通工程学大量的研究,交通流三参数数据为相关性较高[16]的随机变量。如果使用普通高斯算法,则无法表征特征向量之间的关联性;多元高斯分布模型则可以自动捕获特征之间的相关。本文提取速度和流量二元特征,而每日的样本数量144远大于特征数量2,因此满足使用多元高斯异常检测算法的前提条件。
对于训练集二元随机变量X1=(V,Q),具备如下的概率分布密度函数:
(1)
式中:n为特征向量(速度和流量)的数量,取2;μ为对应特征向量的均值;Σ为二元特征数据集的协方差矩阵。
根据多元高斯模型的公式,使用matlab编程计算出X1=(V,Q)的参数μ和Σ,从而拟合出模型p(x)以及阈值参数ε。然后,将测试数据集输入该模型p(x),计算出对应点p(x)的值。通过比较计算出p(x)值与模型异常阈值ε,当p(x)<ε时,判断对应的数据点为异常值,否则为正常值。
2 基于GM(1,1)-Markov的数据修正
2.1 小时修正窗口的引入
通过异常检测算法,可得到原始数据集中的异常点。假设存在异常点xi,xj,xk,,其中i,j,k,分别表示上节检测出的异常点在原始数据集中的角标编号。
针对每1个异常数据点,分别建立小时修正窗口,即每个窗口(含异常点)有6个数据。根据GM(1,1)模型的特点,第1个数据点为基准点,不会被拟合计算。因此每个异常点有5种不同的修正窗口。用W分别表示这些窗口为:W=[xi-5,xi-4,xi-3,xi-2,xi-1,xi],[xi-4,xi-3,xi-2,xi-1,xi,xi+1],[xi-3,xi-2,xi-1,xi,xi+1,xi+2],[xi-2,xi-1,xi,xi+1,xi+2,xi+3],[xi-1,xi,xi+1,xi+2,xi+3,xi+4]。
经过大量的实验运算,得出选取将异常点作为窗口最后1个数据的修正窗口得到的修正值为最优。若首次修正效果不满足异常检测,则依次选取其他形式的修正窗口进行异常点再修正。
2.2 修正窗口数据集波动性处理
当数据出现波动性变化时,GM(1,1)模型的拟合效果会受到影响,因此采取1种补加增量的方法,弱化原始数据的随机性,提高灰色模型的运算精度。

(2)
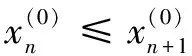
(3)
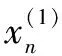
2.3 GM(1,1)-Markov模型
通过GM(1,1)灰色模型的拟合,找出数据的外在变化趋势;进一步利用马尔可夫模型,挖掘时序数据内在状态的转移规律。具体步骤如下:
1)对数据集X(1)进行1次累加处理:
(4)
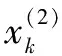
2)定义邻值生成数:
(5)
式中:zk为X(2)的邻值生成数列。
3)建立GM(1,1)模型:
(6)
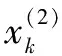
(7)
式中:α为发展系数,β为灰作用量。用回归分析求α,β的值。可得:
(8)
(9)

4)还原原始数据修正值:
(10)
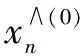
5)求出窗口修正数据集的相对残差:
(11)
式中:k=1,2,,n。
6)划分状态区间:根据相对残差范围集中程度进行划分。假设划分好的区间为E1,E2,Ej,j为区间的个数。
7)确定状态转移矩阵:
(12)
式中:Pab为状态Ea转移到状态Eb(b>a)的转移概率;mab表示由Ea一步转移到Eb出现的次数,Ma表示状态Ea出现的总次数。确立1步状态转移矩阵:
(13)
Pk=v0·P
(14)
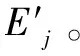
(15)
式中:λ+η=1,本文使用平均权值。
2.4 断面交通异常数据质量控制
对于断面交通异常数据,运用上述算法,建立整套质量控制流程如图1所示。算法总体分为2大部分,即异常检测与数据修正。

图1 交通异常数据质量控制流程Fig.1 Quality control procedure of traffic abnormal data
3 样本实验
选取汕昆高速K2077断面数据,样本数据集为2018年5月该断面的交通流量以及速度数据。首先,对原始数据进行标准化处理及二元特征提取,5月1日部分标准化数据如表1所示。
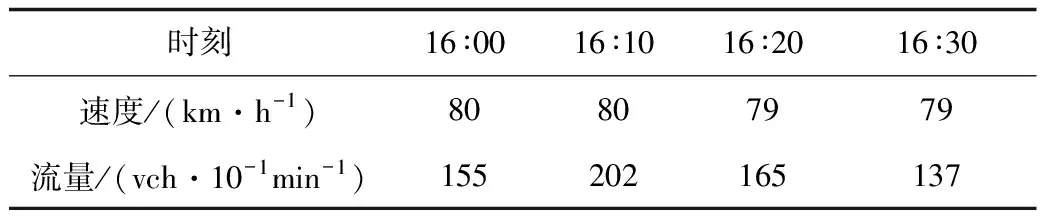
表1 样本部分标准化数据Table 1 Partial standardized data of sample
为了便于二元高斯模型的训练,将所有流量数据乘以0.5,做归一化处理。
3.1 异常检测
使用5月1日数据集作为二元高斯模型训练集,5月2日数据集作为验证集。模型训练后得出异常检测阈值ε=1.735 759e-04。检测出验证集中异常数据角标编号分别为9,24,40,49,126,128,139共计7个异常数据点。二元高斯模型异常检测程序在matlab中运行结果如图2所示。
为验证此异常检测算法的有效性,继续使用5月3日、5月4日、5月5日数据作为测试集。分别检测出对应数据集异常值,并计算出对应的误检率和检测率,如表2所示。
通过对上述4天交通数据进行二元高斯分布异常检测,其结果表明:模型异常检测率均值可达83.13%,而其中误检率均值仅为11.75%。
3.2 数据修正
对5月2日数据集检测出的异常点,进行修正窗口划分,将这些异常修正窗口在全天数据集中标记出来,如图3所示。每一个窗口具有6个数据,异常数据点置于末端。

图2 异常检测模型可视化结果Fig.2 Visualization results of anomaly detection model

检测指标日期5月2日5月3日5月4日5月5日均值误检率121361611.75检测率87.580818483.13
波动性处理前后灰色(1,1)模型拟合平均相对误差对比如表3所示,由表3中数据可知,直接使用灰色模型对窗口数据进行处理,则各修正窗口拟合平均相对误差的均值在20%以上。经过波动性处理优化之后,灰色模型各窗口平均相对误差的均值不足10%。
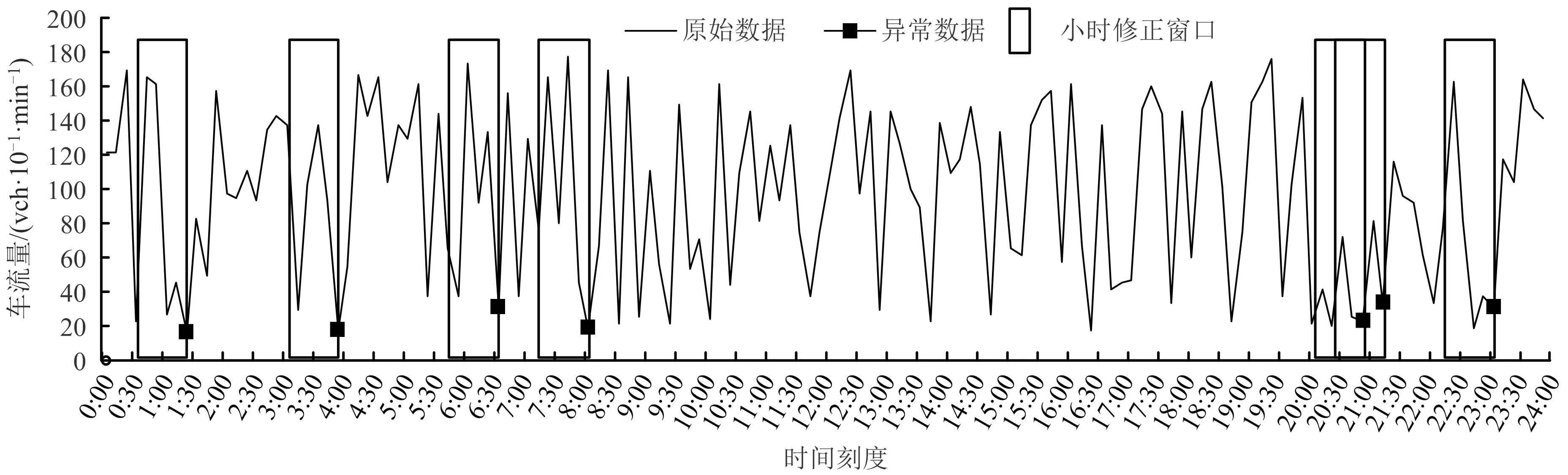
图3 划分修正窗口Fig.3 Partition of correction windows

模型窗口窗口1窗口2窗口3窗口4窗口5窗口6窗口7均值GM(1,1)21.0716.1845.339.9315.6925.6322.5322.34优化GM(1,1)3.686.8129.055.8110.152.709.779.71
各个窗口的修正过程如图4所示。由于最终的修正数据集更新只针对异常点,因此窗口的其他点只参与状态转移的概率划分,而不计算其最终的马尔可夫调整量。

图4 各窗口模型修正Fig.4 Model correction of each window
3.3 结果论证
为了验证本文提出的优化GM(1,1)-Markov修正方法的有效性,选取历史数据修正和移动平均修正2种方法作为对比论证。每种方法修正的数据分别与对应窗口的数据集平均值做绝对误差(Absolute Error)、相对误差(Relative Error)、以及均方根误差(Root Mean Squared Error)计算。3种方法对异常点的修正误差分析如表4所示。
通过上述3种交通数据修正方法的误差分析,得出波动性优化GM(1,1)-Markov深入挖掘了原始数据集的内在规律,算法误差小且具备很强的鲁棒性。在不使用大量历史数据的前提下,能够起到良好的修正效果。
4 结论
1)以断面数据的时间刻度为标签,提取该标签数据的二元特征向量,即速度和流量,运用二元高斯分布拟合的模型,快速准确地检测出异常数据。今后还可以推广到多元特征向量,例如涵盖交通检测器常有的占有率数据集。
2)对异常数据进行针对性修正,引入小时窗口既使得修正过程清晰便捷又避免大量冗余数据的复合运算。采用GM(1,1)-Markov则可以在小时窗口内部较好地表征出异常点的客观规律变化,从而进行修正。
3)鉴于短时交通数据的随机波动性大,引入波动性优化处理弥补了GM(1,1)-Markov模型局部失真的缺陷。

表4 修正数据误差对比Table 4 Error comparison of corrected data
