考虑爆裂影响的钢筋混凝土梁火灾温度场数值分析*

许文龙，周 戟,2，刘朝峰,2，刘才玮，杜金泽

(1.河北工业大学 土木与交通学院，天津 300401；2.河北工业大学 河北省土木工程技术研究中心，天津 300401；3.青岛理工大学 土木工程学院，山东 青岛 266033)

0 引言

钢筋混凝土梁是结构的主要承重构件，也是火灾受损最为严重的构件之一[1-2]。虽然混凝土具有良好的热惰性，但在火灾或高温下易发生爆裂现象[3-4]。火灾下混凝土爆裂，构件有效截面减小，钢筋温度骤升致使其快速软化屈服，降低构件或结构的承载能力，引起结构破坏或倒塌[2]。因此，火灾下混凝土爆裂对构件的承载能力影响重大，非常有必要开展爆裂对钢筋混凝土梁的抗火性能研究。

自首次发现混凝土高温爆裂现象[5]以来，国内外学者对混凝土高温爆裂机理、影响因素进行了大量研究。得出爆裂的机理基本分为以下3种：①温度梯度引起水汽迁移并在构件内某一截面凝结形成饱和蒸汽带，从而使蒸汽压积聚诱发爆裂；②温度梯度使内外截面产生应力差，致使表层部分混凝土块在应力作用下发生爆裂；③多物理场耦合作用下导致爆裂。从目前的研究可以看出关于混凝土爆裂机理尚未形成学术界统一的共识，且学者大多采用小比例试验构件进行研究，试验结果不能真实反映结构在火灾中的力学性能[6-8]。对于火灾下混凝土爆裂对钢筋混凝土构件抗火性能的研究还不成熟，缺乏真实火灾下钢筋混凝土梁等受弯构件爆裂影响分析。项凯等[9]采用试验验证的有限元模型，分析了混凝土爆裂面积比、爆裂深度、爆裂位置对轴心受压圆形截面钢管混凝土叠合柱耐火性能的影响规律；侯一钊等[10]采用有限元数值模型分析了考虑不同的爆裂情况对火灾后高性能混凝土剪力墙残余抗剪承载力的影响；金健等[11]采用有限元软件ABAQUS，基于一次爆裂模式提出了考虑爆裂深度、爆裂长度、爆裂开始时间等爆裂参数对高强混凝土柱轴向位移、截面温度场和耐火极限的影响规律；张岗等[12]分析了高温爆裂对预应力混凝土箱梁截面温度场的影响，计算了不同爆裂指标下箱梁的极限承载力；王丽等[13]通过有限元模拟研究了爆裂现象对构件温度的影响，对比分析了ANSYS温度模拟结果和试验测试结果；申中原等[14]通过对矩形混凝土梁的控制截面进行离散分析，推导了火灾下考虑爆裂的梁极限承载力计算公式。可见，目前针对钢筋混凝土柱、叠合柱、板等构件进行了高温爆裂对构件抗火性能的分析，针对钢筋混凝土梁受弯构件的爆裂影响分析还比较少。因此，本文依据钢筋混凝土梁火灾试验，建立钢筋混凝土简支梁数值分析模型，分析火灾下爆裂参数对钢筋混凝土梁控制截面温度场的影响规律，为分析爆裂对混凝土梁力学性能影响提供支持。

1 试验概况

简支梁截面尺寸为250 mm×400 mm，长度为3 000 mm，采用φ35混凝土，HRB400钢筋，混凝土保护层厚度30 mm，混凝土、钢筋的材料参数见文献[15]，试件配筋及尺寸示意如图1所示。

图1 试件尺寸及1-1截面配筋Fig.1 Specimen size and cross secation 1-1 of reinforcing bars

为确保试件内部水分维持平衡，将其放入温度不低于15 ℃，相对湿度不高于75%的环境中养护。试件在水平火灾炉中进行3面(底面及两侧面)受火试验，试验方案及过程详见文献[15]，混凝土温度由预先埋入试件中的自制镍铬-镍硅K型热电偶测量，具体布置如图2所示。

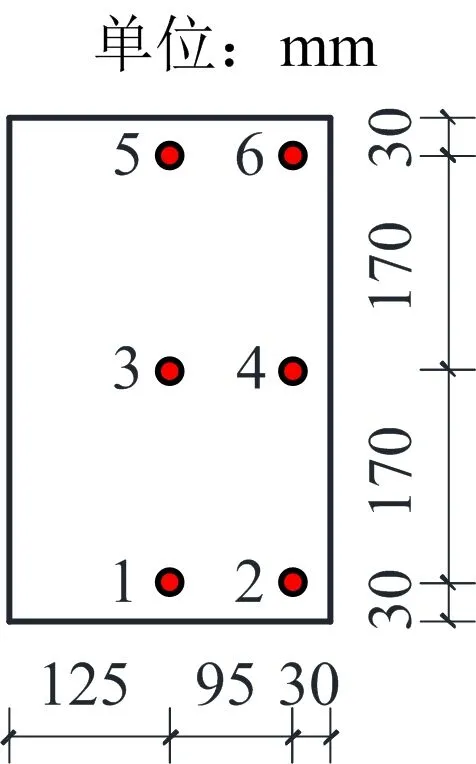
图2 热电偶布置示意Fig.2 Schematic layout of thermocouples

火灾过程采用ISO-834标准升温曲线调控，初始温度为20 ℃，实际受火时间设定为150 min，然后试件自然冷却至常温。加热到15 min左右时，试件3个受火面有水分蒸发现象；加热到20～40 min时，试件发生不同程度上的爆裂，如图3所示。火灾试验中发生的爆裂，跨中、两角部位爆裂面积较大，但是未出现钢筋裸露。

图3 试件火灾爆裂现象Fig.3 Fire spalling phenomenon of specimen

2 钢筋混凝土梁数值模型分析

2.1 材料热工参数

温度场模拟分析是高温下热力耦合分析的基础。本文以上述混凝土简支梁为模拟对象，建立高温下钢筋混凝土梁的有限元模型，研究火灾爆裂对钢筋混凝土梁温度分布的影响规律。混凝土高温下的导热系数、比热容及密度等参数取值可参考《建筑钢结构防火技术规范》[16]，热膨胀系数采用Lie的设定取值[17]。钢筋高温下的导热系数、比热容采用李引擎的计算模型[18]，热膨胀系数采用陆洲导的计算模型[19]。

2.2 边界/荷载条件

升温前，结构温度为环境温度(即20 ℃)且无热量转移。受火时梁体2个侧面及底面通过热辐射、热对流进行热交换，梁体内部通过热传导进行热量转移[1]。热对流以面荷载形式施加，对流换热系数为35 W/(m2·℃)；辐射率系数取值为0.8，斯蒂芬-波尔兹曼常数为5.67×10-8W/(m2·K4)；升温曲线采用ISO834标准升温曲线。

混凝土在火灾作用下具有随机不确定性特点，爆裂发生也具有时间与区域的不确定性。学者普遍观测或设定爆裂发生的平均初始时刻约为15 min左右[3,6,9,11-13,20]，爆裂一般发生在混凝土保护层内，深度范围约在0～30 mm之间[9-13,21-23]；数值模拟分析利用ANSYS建立钢筋混凝土简支梁的热分析有限元模型，采用“单元生死”的方法模拟火灾下混凝土的爆裂，即受火15 min时将爆裂区域单元“杀死”，同时将热边界条件赋予爆裂完成后的受火面。

3 梁的温度场模拟及试验分析

图4为钢筋混凝土简支梁在三面受火时，30，60，90，120 min的截面温度分布云图。总体来看，温度场等值呈现为“U”型分布，随着升温时间的增加，混凝土梁的温度逐渐增高，等温曲线逐渐向光滑的“U”型过渡。

图4 钢筋混凝土简支梁的截面温度分布Fig.4 Cross-section temperature distribution of reinforced concrete simply supported beam

由于试验火炉升温达不到标准升温曲线水平，应将试验测定的升温时间转化为等效爆火时间。等效爆火时间为与实际升温曲线下方的面积相等的标准升温曲线所对应的时间[24]。实际试验炉内温度变化与在ISO 834标准下的升温曲线对照如图5所示。图6为钢筋混凝土梁跨中截面温度测点的实测与模拟曲线，其中带*标记的为有限元模拟温度。试验下的测定数据已转化为等效爆火时间下温度变化。

图5 试验炉温与标准升温曲线Fig.5 Testing furnace temperature and standard fire temperature-time curve

图6 梁截面中测点温度实测与模拟对比Fig.6 Comparison of measured and simulated temperatures at measurement points in beam cross-section

由图6可知，测点1～5的数值模拟与试验测得的温度曲线发展趋势基本一致，但测点6的实测温度曲线与模拟曲线偏差较大，究其原因：①试验炉上部盖板与梁之间缝隙填充防火岩棉，导致6号测点受热不充分(见图3)；②防火岩棉有一部分依附于梁体上部表面，也可能阻碍表面受热(见图3)；③热电偶埋设误差等原因。总体来看，模拟温度与试验测点温度基本一致，试验中在150 ℃温度上升明显缓慢，出现温度台阶，试验数值较模拟数值小。可能是模拟中未考虑水分蒸发和迁移等因素。

4 爆裂参数对温度场分布的影响

结合试验现象以及荷载不利分布原则选取以下爆裂工况：假定一次集中爆裂，爆裂时刻取15 min；爆裂深度取0，10，20，30 mm；爆裂面积比(即爆裂的混凝土面积与受火区混凝土总面积的比值)取0%，6.7%，13.3%，20%，100%。爆裂位置参数：爆裂连续、位于梁跨中处(位置1)；爆裂连续、位于梁支座处(位置2)；爆裂不连续、位于跨中和支座处(位置3)；爆裂连续、覆盖全表面(位置4)；梁不发生爆裂(位置5)。

4.1 爆裂深度对梁的温度场分布的影响

假定全截面爆裂，爆裂位置取跨中，考虑不同的爆裂深度，梁截面温度场的影响曲线(取跨中纵向钢筋处为温度测点)，如图7所示。

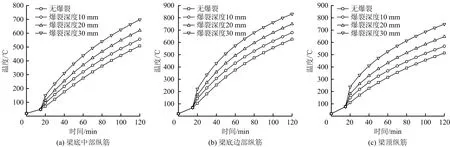
图7 爆裂深度对截面纵筋处温度的影响Fig.7 Influence of spalling depth on temperature at cross-section longitudinal bar

由图7可知，混凝土爆裂对截面内温度场的分布影响较大，爆裂深度越大，截面内温度越高；随着爆裂深度增大，受火时间相同的截面升温差值逐渐增大。在同一爆裂深度下，同一时刻截面内底部边筋较中筋处温度高。

4.2 爆裂面积比对梁的温度场分布的影响

爆裂深度取20 mm，爆裂位置取梁跨中，假定梁体受火面周长方向全爆裂，考虑不同爆裂面积比(0%，6.7%，13.3%，20%，100%)得到爆裂面积比对截面内温度场的影响，如图8所示。

总体来看，爆裂面积比对截面内温度具有一定影响；当爆裂面积比较小时，截面内温度变化较大，但随着爆裂面积比的增大，截面内温度增加差值逐渐减小(即爆裂面积比对温度的影响作用迅速衰减)，在爆裂面积比为13%左右时截面内温度基本达到最大值。

图8 爆裂面积比对截面纵筋处温度的影响Fig.8 Influence of spalling area ratio on temperature at cross-section longitudinal bar

4.3 爆裂位置对梁的温度场分布的影响

爆裂深度取20 mm，爆裂面积比取13.3%，考虑爆裂位置变化：即爆裂位置连续、位于梁跨中处(位置1)；爆裂位置连续、位于梁支座处(位置2)；爆裂位置不连续、分别位于跨中和支座处(位置3)。同时设置对照组：即爆裂位置连续、覆盖梁纵向全截面(位置4)；梁表面不发生爆裂(位置5)，得到爆裂位置与跨中截面温度曲线，如图9所示。

图9 爆裂位置对跨中截面纵筋温度的影响Fig.9 Influence of spalling location on temperature at longitudinal bar in mid-span section

由图9可知，在爆裂面积比、爆裂深度一定的情况下，跨中发生爆裂对跨中截面温度场影响较为明显，接近于梁体表面全爆裂的情况；而支座处发生爆裂对跨中截面温度场影响较小，接近于梁体表面无爆裂的情况；跨中、支座处同时发生不连续的爆裂，跨中截面底部纵筋温度，介于上述2种工况之间，偏向于跨中发生爆裂的情况，但是对跨中截面顶部纵筋温度的影响，基本上和跨中发生爆裂、梁体全表面发生爆裂的温度场相同。可见，与全表面发生爆裂相比，随着爆裂位置逐渐接近跨中位置，跨中截面温度逐渐升高，但是底部纵筋处温度较顶部纵筋处温度升高较快。

5 结论

1)梁截面各测点温度模拟值与试验实测值基本吻合，但测点6的温度实测值与模拟值偏差较大，可能是盖板或防火岩棉阻碍其表面受热，或未考虑水分蒸发和迁移、混凝土爆裂对测点温度的影响，热电偶的埋设位置误差等原因造成的。

2)混凝土爆裂对截面内温度场的分布影响较显著，爆裂深度越大，截面内温度越高；爆裂面积比对截面内温度具有一定影响，当爆裂面积比较小时，截面内温度变化较大，当爆裂面积比为13%左右时，截面内温度基本达到最大值；随着爆裂位置逐渐接近跨中位置，跨中截面温度逐渐升高，但是底部纵筋处温度较顶部纵筋处温度升高较快。

3)数值模拟未考虑真实火灾效应，后续将研究不同燃烧模式升温曲线与标准升温曲线转换的量化关系，进而细化模拟分析真实火灾下梁的温度场分布的变化规律。