基于神经网络的股票收益率预测研究

潘水洋，刘俊玮，王一鸣

（北京大学经济学院，北京100871）

0 引 言

从计量经济学角度在对传统线性资产定价模型进行实证分析时,发现该模型的解释能力不足：或者回归截距项显著大于零，或者贝塔系数不显著等。造成这些问题的根源可能是解释变量遗漏，也可能是贝塔系数或随机项方差的时变性等。因此,针对线性资产定价模型的修正出现了3个不同的努力方向：将失败归因于解释变量的遗漏，据此提出了多因子资产定价模型[1-3]；将失败归因于贝塔系数的时变性，据此提出了变参数(贝塔)资产定价模型[4]；将失败归因于随机项方差的时变性，据此提出了GARCH类资产定价模型等[5]。然而上述3模型并没有从根本上解决资产定价模型解释能力不足的问题。首先，单纯依靠增加解释变量提高模型解释能力是一个无穷尽的过程。其次，由时变贝塔参数定价模型估计出的贝塔系数和市场组合的超额收益之间的协方差并不大，这意味着时变贝塔参数定价模型得到的收益和用CAPM模型计算出来的收益相仿[6]。

与此同时，国内外学者发现金融市场存在非线性特征，大量文献对此进行了实证检验和报道[7-10]。股票市场具有非线性特征意味着随机游走与有效市场假设将失效，以此为理论假设基础的现代资本市场理论以及其他依赖正态分布或有限方差性质的金融计量学模型都将面临质疑。令人遗憾的是，在资产定价模型的修正过程中，股市具有非线性现象这一金融异象被选择性地忽视了，未被纳入模型框架，其挑战在于现有模型无法刻画因子间的非线性定价结构。为解决这一问题，笔者创新性地引入机器学习领域中的神经网络模型，以捕获市场组合收益率、市值和账面市值比三因子之间的非线性定价结构。对本模型的样本外拟合优度、多空策略业绩表现与经典Fama-French三因子模型做了比较。实证结果表明：神经网络模型能精准捕获市场组合收益率、市值和账面市值比3个因子之间的非线性关系。神经网络非线性模型在样本外拟合优度、多空策略业绩上均要优于传统三因子线性定价模型。本文的贡献主要体现在：（1）脱离了依靠增加解释变量个数提高线性资产定价模型解释力的传统实证资产定价的研究框架。（2）将机器学习领域中的神经网络模型运用于金融资产定价领域，实现定价因子之间的非线性关系捕获，丰富了资产定价的研究方法。（3）采用机器学习理论的非线性资产定价模型能够更加准确地预测我国股票投资组合的收益率，对投资者构建有效投资策略具有较强的借鉴意义。

1 神经网络非线性定价模型

与传统金融计量经济学方法相比，机器学习理论中的神经网络模型更关注预测结果，不关注估计量的渐进性质，因此将机器学习模型应用于资产定价领域，须针对研究的问题构造合适的实证框架[11-13]。

学术界提出的随机贴现因子资产定价模型的一般表达式为

式(1)中，Mt+1表示随机贴现因子，可表示为风险因子的函数。随机贴现因子与风险因子之间的函数关系可能为线性关系，也可能为非线性关系。当随机贴现因子是风险因子的线性组合时，资产的收益可用线性因子模型(即贝塔模式)来刻画。当随机贴现因子不是风险因子的线性组合时，以上结果并不成立。从本文引言部分可知，大量实证文献均发现股票市场存在非线性特征，为了更好地刻画资产定价模型，实现理论与实践的完美结合，随机贴现因子应当满足：Mt+1不仅能识别线性定价结构，而且也能识别非线性定价结构。本文通过引入机器学习中的神经网络模型来实现Mt+1的非线性映射。

1.1 神经网络模型

机器学习中的神经网络结构由输入层、隐含层、输出层组成。假设有N个任意样本集(xj,yj)，j=1,2…,N。其中，

通过神经网络可以自动寻找x与y之间的非线性映射关系。对于图1中具有L个隐含结点的单隐层神经网络的输出tj可以表示为

式（4）中，g为激活函数，一般为σ函数。wi=[wi1,wi2,…,win]T为第i个隐层单元的输入权重，bi为第i个隐层单元的偏置，θi=[θi1,θi2,…,θim]T为第i个隐层单元的输出权重。tj=[tj1,tj2,…,tjm]T为神经网络预测输出值。上式的矩阵形式为

其中，

单隐层神经网络对输入的N个样本集(xj,yj)，j=1,2，…,N进行自我学习，通过最小化输出值与实际值的误差平方和估计参数得 到x与y之间的非线性映射关系：

式(9)等价于最小化损失函数：

式(10)无解析解，采用梯度下降法可得到模型参数估计。

1.2 神经网络非线性定价结构辨识

将神经网络模型应用于资产定价的一个重要原因是该模型能刻画股票市场的非线性现象。假设市场存在M只股票，股票的定价因子有N个，在t时刻，拥有股票因子数据集Xt及股票收益率yt：

资产定价的实质就是找到因子数据集Xt与股票收益率yt之间的映射关系F：

线性资产定价模型：假设因子数据集Xt与股票收益率yt之间存在线性关系，此时式(10)变为

神经网络非线性资产定价模型：假设因子数据集Xt与股票收益率yt之间存在非线性关系:

式(13)中,W，b，θ为神经网络模型中的待估计参数，F为式(5)所描述的神经网络非线性映射。对比式(12)和(13)发现，与传统线性资产定价模型相比，神经网络资产定价模型能捕获到因子数据集Xt与股票收益率yt之间的非线性映射关系，非线性映射通过以下激活函数实现：

只要因子数据集Xt与股票收益率yt之间存在非线性定价结构，含有多个隐含层的神经网络结构从理论上就能够辨识隐藏在数据背后的非线性定价结构。下文将同时运用Fama三因子线性定价模型和神经网络非线性资产定价模型对我国A股市场进行实证分析，通过比较两模型的样本外拟合优度和多空策略业绩来检验神经网络定价模型的有效性。

2 实证分析

选取Fama-French三因子资产定价模型作为基准模型，通过对比分析检验神经网络非线性定价模型的有效性。该模型在国内外股票市场有大量的实证检验[1-3,14-15]。

Fama-French三因子资产定价模型中，股票收益率可由市场组合收益率、市值、账面市值比进行解释。根据此理论，构建三因子线性定价预测模型:

式(15)中，rit表示股票i在时间t时的收益率；Rm,t-1表示在时间t－1时按市值加权形成的市场组合收益率；Sizei,t-1表示股票i在时间t－1时的流通市值；Btopi,t-1表示股票i在时间t－1时的账面市值比；eit表示三因子定价线性预测模型预测误差；β0，β1，β2，β3为线性定价模型参数。对市场组合收益率、市值、账面市值比等定价因子在每个横截面上均减去均值并除以标准差，进行归一化处理。

为检验神经网络资产定价模型的有效性，采用样本外模型预测值的拟合优度R2、Diebold-Mariano检验以及构建多空策略业绩表来检验模型的有效性，基准模型为Fama-French三因子线性定价模型。评判模型优劣的标准有：

（1）样本外拟合度R2，R2越大，模型越优。

（2）Diebold-Mariano检验。

（3）多空投资策略。

在模型输入变量保持不变的前提下，如果以上3条均较优，就有足够的理由认定神经网络资产定价模型能够识别隐藏在定价因子数据下的非线性关系，非线性定价模型优于线性定价模型。

2.1 模型样本外拟合度比较

选取1997年1月至2017年12月沪深两市A股股票的月度收益率、收盘价、合并财务报表中流通股、总股本、所有者权益合计数据，剔除*ST、已退市、上市不足1年的股票。收盘价与流通股数量相乘得到股票流通市值；收盘价与总股本相乘得到股票总市值；所有者权益合计除以股票总市值得到账面市值比。市场组合收益率采用中证全A指数收益率。所有因子在横截面上减去均值除以标准差做归一化处理。本文的数据来源于wind资讯数据库。

将1997年1月至2007年12月的数据作为模型训练数据，用于估计Fama-French三因子线性定价模型参数和神经网络非线性资产定价模型参数。将2008年1月至2017年12月的数据作为样本外验证数据，用于检验模型样本外的预测能力。估计模型参数后，从2008年1月开始，在每月月初，将股票最新的市值因子数据、账面市值比因子数据、中证全A指数月度收益率数据分别输入Fama-French三因子线性定价预测模型、神经网络非线性资产定价预测模型，得到每个模型下个月股票收益率的预测值，再计算模型样本外的拟合优度R2，拟合优度计算公式为

式(15)中，ri,t表示第i只股票在t时刻的实际收益率，表示第i只股票在t时刻的预测收益率。表1为Fama-French模型和神经网络模型股票收益率样本的外拟合优度，其中NN1～NN5分别表示采用1～5层隐含层神经网络结构非线性定价模型，输入层均为3个节点（分别代表市场组合收益率、市值、账面市值比3个因子），输出层均为10个节点(用于股票收益率预测分组)。NN1隐含层含有32个节点，NN2隐含层分别含有32，16个节点，NN3隐含层分别含有32，16，8个节点，NN4隐含层分别含有32，16，8，4个节点，NN5隐含层分别含有 32，16，8，4，2个节点。采用非线性激活函数式（14）实现。由表1知，不同隐含层数神经网络模型样本的外拟合优度均高于Fama-French模型样本。

表1 模型样本外拟合优度Table1 Goodness of fit outside sample

2.2 Diebold-Mariano检验

用2008年1月至2017年12月的数据作为样本外验证数据，采用预先训练好的模型预测股票下一期收益率，在此基础上，用Diebold和Mariano对不同模型两两之间进行配对检验，比较不同模型之间的预测能力，结果如表2所示。从表2第2行可以看出，具有不同隐含层的神经网络非线性资产定价模型样本的外预测能力均要好于Fama-French三因子线性定价模型。隐含层数不同的神经网络非线性资产定价模型之间无显著性差异。

表2 Diebold-Mariano配对检验Table 2 Diebold-Mariano pairing test

2.3 多空策略业绩比较

为了进一步检验神经网络模型的有效性，本文基于Fama-French模型、神经网络模型构造多空策略组合：Fama-French因子线性组合预测策略和神经网络因子非线性组合预测策略。

Fama-French因子线性组合预测策略构造过程：每个月初，Fama-French模型基于最新因子截面数据预测股票下一期收益率，然后将股票收益率预测结果按降序排列等分为10组，做多第1组股票，做空第10组股票。

神经网络因子非线性组合预测策略构造过程：每个月初，神经网络模型基于最新因子截面数据预测股票下一期收益率，然后将股票收益率预测结果按降序排列等分为10组，做多第1组股票，做空第10组股票。

表3 分组收益Table 3 Group's return

表4 分组收益Table4 Group's return

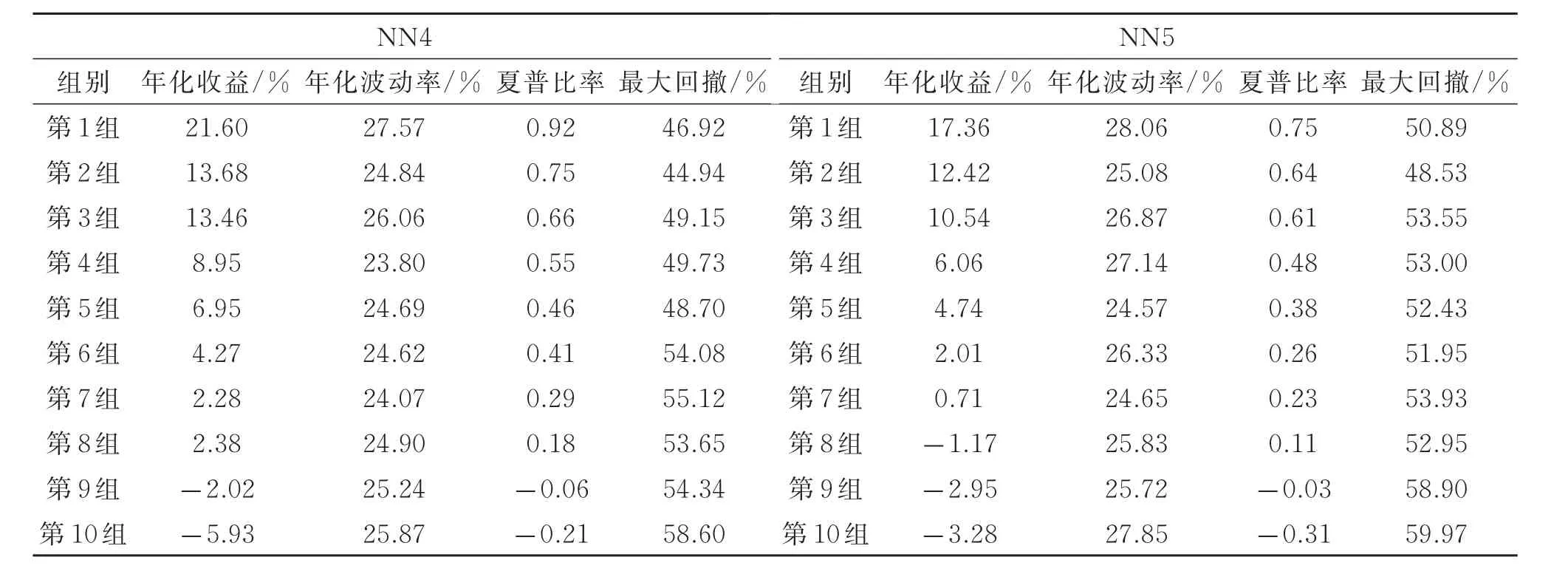
表5 分组收益Table 5 Group's return

表3～表5为各个模型策略的分组表现。从策略分组表现看，由于Fama-French分组策略未能捕获到因子之间的非线性定价结构，导致第5组收益率高于第4组，第9组收益率高于第8组，组间收益率并未呈现递减关系。与此相对应的是，神经网络分组策略能够捕获到因子间的非线性定价结构，其预测准确率要好于Fama-French分组策略：从第1组到第10组，收益率表现出严格的递减规律，且第1组(多头)收益率均高于Fama-French三因子模型第1组，第10组(空头)收益率均低于Fama-French三因子模型第10组。

表6为各模型做多第1组、做空第10组的多空策略表现。从表6中可以看出，神经网络模型多空策略年化收益、年化波动率、夏普比率、最大回撤均要好于Fama-French模型。进一步表明，神经网络模型捕获到了因子之间的非线性关系，策略表现要优于Fama-French模型。

3 结 论

针对股市具有非线性特征，在资产定价模型的修正过程中易被选择性忽视，创新性地将机器学习领域中的神经网络模型引入其中，捕获市场组合收益率、市值和账面市值比三因子间的非线性定价结构。新模型与经典Fama-French三因子模型在样本外拟合优度、多空策略业绩表现上进行了对比。实证结果表明，神经网络模型能精准捕获市场组合收益率、市值、账面市值比3个因子之间的非线性关系。神经网络非线性模型在样本外拟合优度、多空策略业绩上均要好于传统三因子线性定价模型。

3.1 中国A股市场存在典型的非线性特征，借助机器学习理论，能够精准捕获定价因子之间的非线性关系。

3.2 机器学习是以数据驱动为核心来构建模型的，并依靠交叉验证选择最优模型，与传统计量经济学方法相比，机器学习更关注预测结果，不关注估计量的渐进性质，因此，将机器学习模型与传统计量模型进行对比时，须针对研究的问题构造合适的实证框架，本文做了初步探索。

表6 分组多空收益Table 6 Group long and short returns